算法性能测试与分析结果

1.问题描述与测试策略

在.NET2003编程环境下用C++实现MFPEA算法，并用其求解TSP问题，所测试数据均来自问题数据库网（http：//www.tsp.gatech.edu/indeX.html）。假定所求解TSP问题的规模为n，在处理TSP问题时采取了以下策略：

1）利用最邻近算法[11]与随机函数生成新个体从而初始化种群；

2）a₀a₁a₂…a_n-1与a₁a₂…a_n-1a₀视为相同模式串，在进行最大频繁子模式挖掘过程中，不能在任意个体中找到元素a_i，使（P´=a_iP∨P´=Pa_i）∧（D（P´）≥e）为真值，则改变搜索方向；

3）采用基于知识的交叉算子进行交叉操作；

4）采用交换和倒序两种变异算子进行变异。

2.参数分析与设置

挖掘间隔代数K对总计算时间及进化结果有重要影响。为了找出相对合适的设置，以pka379为测试问题（最优解是1346.983），对这些参数进行了一定量的统计分析。给定最大进化代数为500，设置不同的K值，分别运行算法20次。对应K值20次的平均时间、所得解平均值、所得解平均值与最优解的比值统计结果见表3-1。观察表可知，随着间隔代数的增加，所得解平均值与平均时间均减小，所得解平均值与最优解的比值增大。这表明间隔代数过短会增加计算时间，不利于加快进化速度；间隔代数过长会造成某些优秀基因无法利用，不利于提高进化质量。综合考虑计算时间与进化质量，选取K=30。

表3-1 不同挖掘间隔代数K所对应进化结果统计

设d与u分别是允许挖掘出的模式长度下界与上界值：①若下限值d比较小且|u-d|也比较小，挖掘出的模式基本上比较短，无从考查这些短模式是否对进化具有推动作用；②若下限值d比较小且|u-d|比较大，包含第①种情况，会获取大量模式；③若下限值d比较大，则|u-d|会比较小，此时挖掘出的模式数量会比较小，甚至没有符合要求的模式，特别是当d值过大，却又挖掘出了相当数量的模式时，随后的进化操作中很容易产生大量相似个体。

在挖掘种群中最大频繁序列模式时，当e的值设置过小时，造成模式过多而影响进化速度；而e的值设置过大时，导致模式数量较少，不利于可持续进化。

由于TSP问题规模从几十到几十万甚至更大的数据不等，对于大规模问题，设置较大的进化种群有利于进化，但种群规模设置过大，会增加计算时间。为使不同的问题具有较合适的进化种群，本研究设计了一种函数[见式（3-4）]确定种群规模N。图3-1示出了函数在n＞100时，函数值在变量空间上的变化趋势。从中不难发现：当n变化显著时，N的变化量比较小。依据此函数设置种群的大小，可以根据问题的规模采用不同的设置。综合考虑，记交叉概率为P_c，变异概率为P_m，并给定e=0.5N+1，d=0.0625L，u=0.25L，K=30，最大进化代数为20000。详细的参数设置见表3-2。

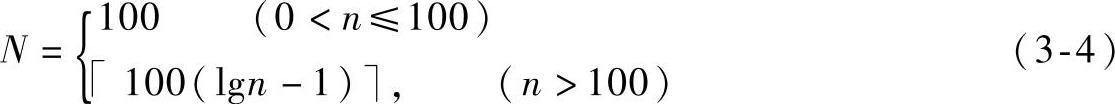
图3-1 n＞100时式（3-4）所表达的函数曲线

表3-2 MFPEA及对比算法HFCSA运行参数设置(www.xing528.com)

3.结果分析

设最优解次数为0_t，最优解为0_p，最优解平均值为0_a，在计算机上将每种算法独立运行20次，最优路径见图3-2，统计结果见表3-3。需要指出的是，本研究在编程实现时，采用的数据类型为float型，表3-3中的最优解除了数据3611.496是本研究所获取的新数据外，其余数据均是按公布的最优路径^[12]推演而得。

表3-3 MFPEA与对比算法HFCSA运行结果统计

从表3-3可知，HFCSA算法^[8]在TSP48问题上，运行20次中有16次获得最优解；但对于kroA100、ch130、ch150、pka379问题，分别以40%、45%、50%、80%的概率出现早熟收敛。它随着问题复杂性的增加，局部收敛的概率逐渐增大，算法的稳定性降低。观察MFPEA对应结果，对于TSP48与kroA100问题获得了20次最优结果，ch130与ch150问题仅一次没有获得最优结果，它们的20次平均值与最优解的差分别为6.707与1.449。虽然pka379问题有6次没有得到最优结果，但其20次平均值与最优解的差只有2.401。

对于Xit1083问题，其他研究者在求解此问题时，计算路径长度的数据类型是整型，已报道的最优路径是3558^[12]，根据已报道的最优路径按float数据类型计算所得结果是3617.262；而本研究提出的算法搜索到的最优结果是3611.496，刷新了此问题的最优记录。此外，对于bva2144问题，同样取得了新最优解。表3-3中此问题MFPEA对应的0_t栏数据是进化结果小于公开记录的次数，它表明本文中提出的算法能够以90%的概率优于当前文献中所给出的最优化解，这也表明MFPEA在洞察决策空间方面具有潜力。需要指出的是，将本研究所得最优结果按整型计算，所得结果为3559，大于公开数据3558。假定存在以下两组数据①4.45、4.35和②4.55、4.05，其和分别是8.8与8.6；将它们整数化后分别是①4、4和②5、4，其对应的和是8与9。正是这种现象的存在，才导致具有较小路径的方案整数化后有较大求和结果。因此，本研究认为采用整型数据类型计算TSP问题可能并不是最好的方式。

针对ch130、ch150、pka379、Xit1083、bva2144问题，根据各算法所得的20个最优解而画的箱线图见图3-3。观察图3-3可知，基于HFCSA的数据所得的箱体体积大，而且数据偏向于上分位点，具有比较长的“须”；基于MFPEA的数据所得的箱体基本趋于一条直线。由这两组数据可以得出：MFPEA在保证搜索的准确性与稳定性、避免早熟收敛方面具有良好表现。

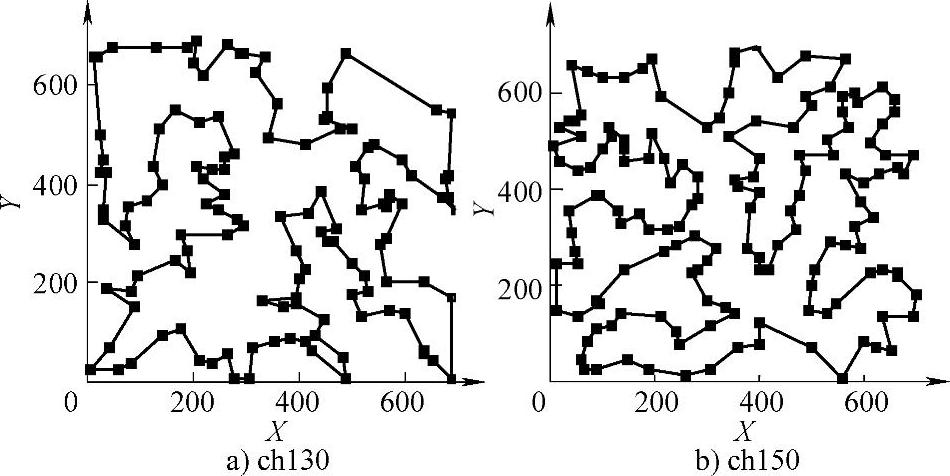
图3-2 部分测试问题采用MFPEA所得最优路径

图3-2 部分测试问题采用MFPEA所得最优路径（续）

图3-2 部分测试问题采用MFPEA所得最优路径（续）

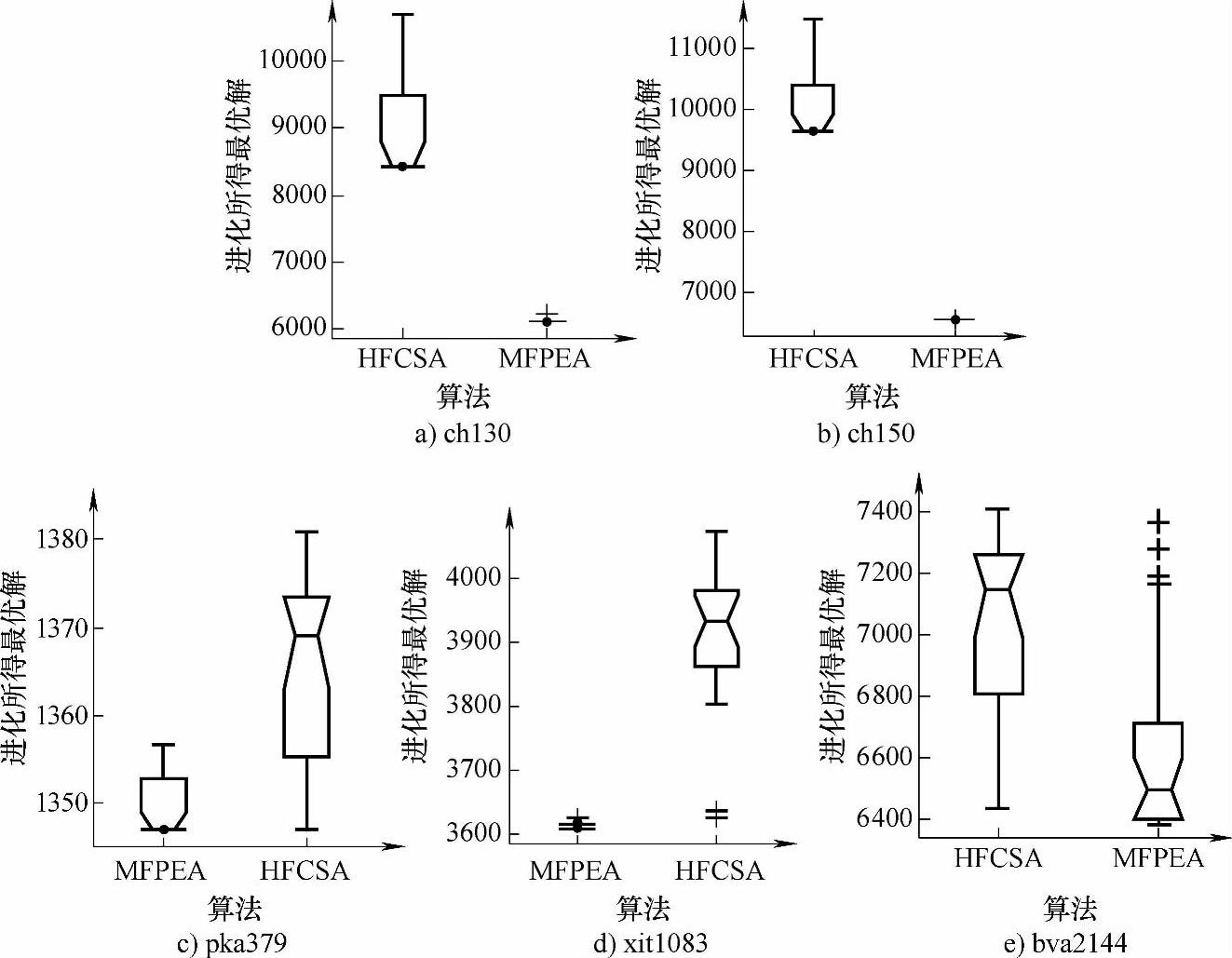
图3-3 HFCSA和MFPEA算法所得结果的箱线图