进化多目标优化算法的典型

1.多目标粒子群算法（MOPSO）

与传统进化多目标优化算法相比，多目标粒子群算法发展较晚，相应的研究成果也比较少。在传统的进化多目标优化研究中，涌现了NSGA-Ⅱ、SPEA2、PESA2等一批优秀的进化算法。而在MOPSO发展历程中，2004年Coello Coello等发表的MOPSO具有历史意义，是国际广泛认可的MOPSO算法。

（1）MOPSO基本框架^[64] MOPSO的基本框架与MOEA类似，具体步骤如下：

1）初始化粒子种群P₀，令t=0，计算粒子种群中个体的目标值，将非劣解保存到外部种群AP_t。

2）初始粒子种群个体的局部最优位置pbest和全局最优位置gbest。

3）修改每个个体的速度和位置，如果粒子飞出搜索空间，调整速度和位置，形成新的P_t，调整粒子的pbest。

4）根据非劣解选择新的外部种群AP_t+1，同时根据相应策略为每个个体选取gbest。

5）t=t+1，判断终止条件。如果满足终止条件则终止，否则转到步骤3）。

对于MOPSO算法，主要面临以下问题：

1）外部种群维护。外部种群一般需要设置种群大小，选择非劣个体存放在AP中，如果非劣解个体超过设置种群大小，需要对外部种群进行修剪。

2）设置自身和全局最优位置。对于单目标优化中，目标解之间存在绝对优劣关系，但面对多目标优化，目标解之间可能没有绝对优劣关系，如何选取较优目标解是研究者关注的重要问题。

3）如何保证粒子群个体始终存在于搜索空间。在粒子飞行过程中，这种飞行存在一定随机性，如何保证粒子一直在搜索空间中飞行而不飞离搜索空间也是需要研究者解决的问题。

对于以上存在问题，众多学者结合多目标优化已有成果逐一进行研究，已经取得很多研究成果。外部种群维护问题与传统的多目标优化算法相似，可以完全按照之前多目标优化算法外部种群存档方式，在此就不展开讨论。对于设置自身和全局最优位置，这是粒子群优化问题的一般特征，其他优化算法不具有此特征。全局最优位置gbest与单目标优化不同，多目标优化问题中不再唯一，因此存在很多彼此不受支配的全局最优位置。研究者已提出了各种有效方法选取全局最优位置。Par-sopoulo^s[89]等提出了向量估计粒子群算法，算法中采用两个粒子种群用于解决两目标优化问题，每个粒子种群根据一个目标进行估计，当根据一个粒子种群调整粒子速度后，用另外一个粒子种群确定跟踪最好粒子。该算法能够优化两目标优化问题，但无法解决更多目标优化问题，存在一定局限性。Coello等^[91]率先为每个至少包含一个外部粒子群个体的网格定义适应度值，然后根据轮盘赌方法选择网格，最后从网格中随机选择一个外部粒子群个体作为全局最优位置^[64]。Alvarez-Benitez等^[102]提出了3种全局最优位置选择方式，分别是ROUND、RANDOM和PROB。ROUND方法将支配粒子群中个体数量最少的档案个体设置为最高优先级，让它们最先成为全局最优位置。RANDOM方法是从支配它的粒子中随机选择一个粒子作为其全局最优位置。PROB方法结合ROUND和RANDOM选择全局最优位置。对于局部最优位置pbest，研究方法比较简单。某个粒子选择局部最优位置时，如果当前位置支配历史局部最优位置则替换局部最优位置，否则局部最优位置不变。当前位置与历史最优位置不存在支配关系时，可通过随机方式选择局部最优位置。在如何保证粒子始终在搜索空间问题中，主要有以下方式：①当某个粒子飞出有效搜索空间时，将当前粒子拖回搜索空间边界线，并改变方向；②在粒子飞出有效搜索空间后，根据粒子群速度公式重新生成速度，直至粒子保证在搜索空间中；③如粒子飞出搜索空间，还可以将其拖回搜索边界附近，然后降低粒子飞行速度。对于保证粒子在有效搜索空间问题解决方案还有很多，对于不同算法可能采用不同的方式，即使同一种算法也可以采用几种方式相结合。

（2）CMOPSO算法描述 之前对MOPSO算法基本框架进行介绍，但并没有涉及具体算法。此处将介绍Coello等提出的MOPSO算法，为了与多目标粒子群算法（MOPSO）区别，将该算法记为CMOPSO，其具体步骤如下：

1）t=0，初始化粒子种群P₀，确定其初始位置和初始速度并计算每个粒子的目标值。

2）将粒子种群P₀非劣解保存于外部种群AP_t中。

3）确定每个粒子的初始局部最优位置pbest。

4）将目标空间分割成许多超立方（又称格子），并根据每个粒子的目标向量确定每个粒子属于哪个超立方。

5）对至少包含一个外部粒子群个体的超立方定义适应度值，然后对每个粒子根据轮盘赌方法选择一个超立方，从中随机选择一个外部粒子群个体作为粒子的全局最优位置gbest。

6）根据标准的粒子群公式更新每个粒子的速度和位置。

7）如果某个粒子飞出有效决策空间，将该粒子拉回决策空间边界线并改变其速度方向。

8）计算粒子种群P_t中每个个体的目标向量。

9）利用Pareto档案进化策略中的自适应网格法对外部种群AP_t进行更新和维护。

10）更新粒子的局部最优解pbest，如果当前位置支配历史局部最优位置则替换局部最优位置，否则局部最优位置不变。当前位置与历史最优位置不存在支配关系时，可通过随机方式选择局部最优位置。

11）t=t+1，如果终止条件成立则停止，否则转到步骤6）。

CMOPSO算法相对于之前的多目标粒子群算法存在一定优势，但是与经典多目标优化算法相比依然存在差距。但Coello提出的MOPSO算法最先发表于国际顶级期刊，因此具有很高的指导意义。

（3）CMOPSO实验结果 为了验证CMOPSO的性能，将该算法应用于一个Benchmark问题并与NSGA-Ⅱ、Micro-GA进行比较。选用GD、SP和ER分别描述算法所获得的解与问题的真实Pareto前端之间的距离、解的分布范围大小以及获得的Pareto最优解个数。

表2-3 三种算法的部分参数设置

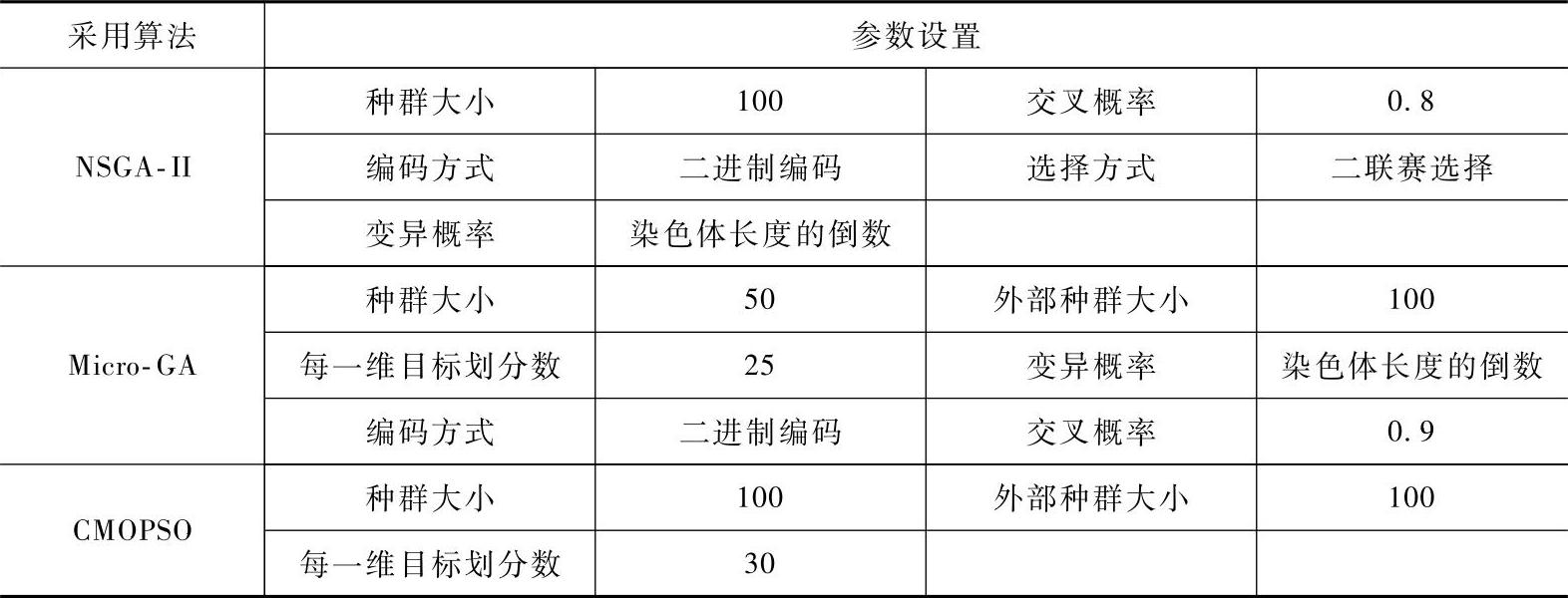
将三种算法按照表2-3的参数设置运行式（2-54）测试函数30次。算法的终止条件为函数评估次数达到5000次。

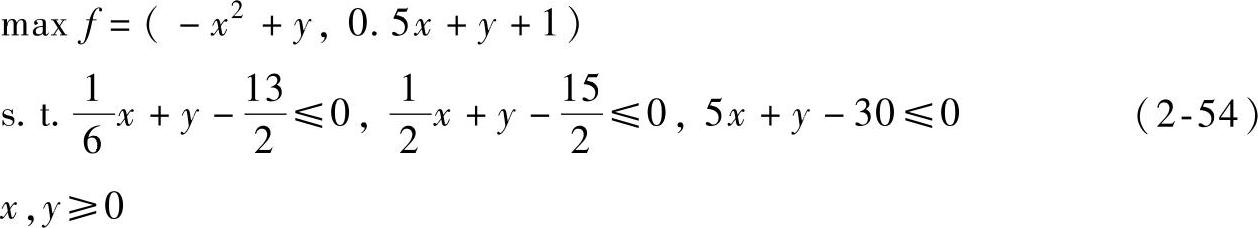
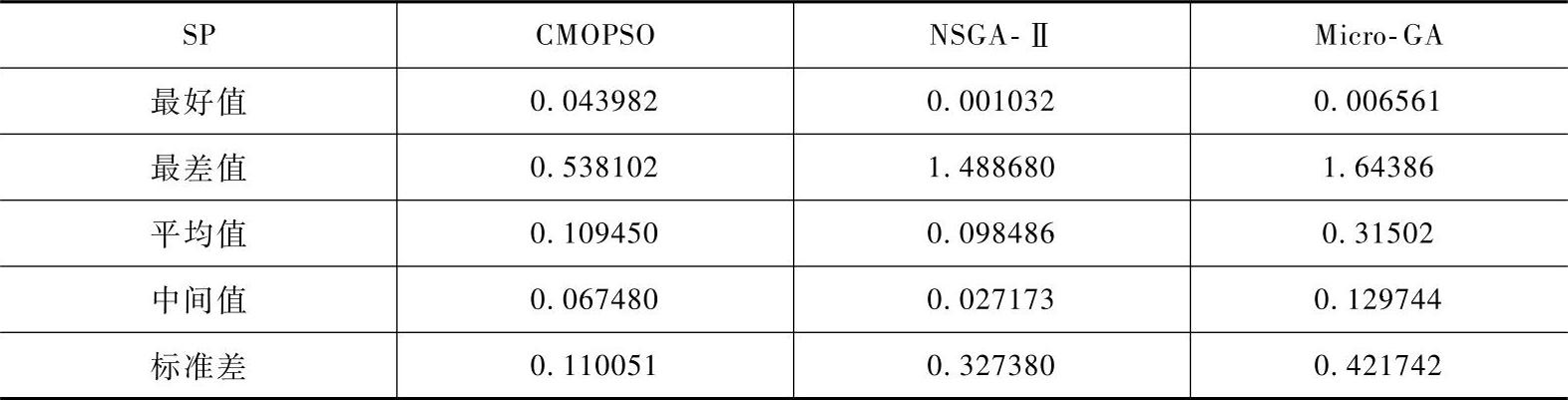
由表2-4～表2-6可以看出，CMOPSO关于指标ER和GD的平均性能是三种算法中最好的，而关于指标SP，CMOPSO的平均值稍低于NSGA-Ⅱ，但CMOPSO的标准差更低。

表2-4 三种算法关于测试函数所得的ER值

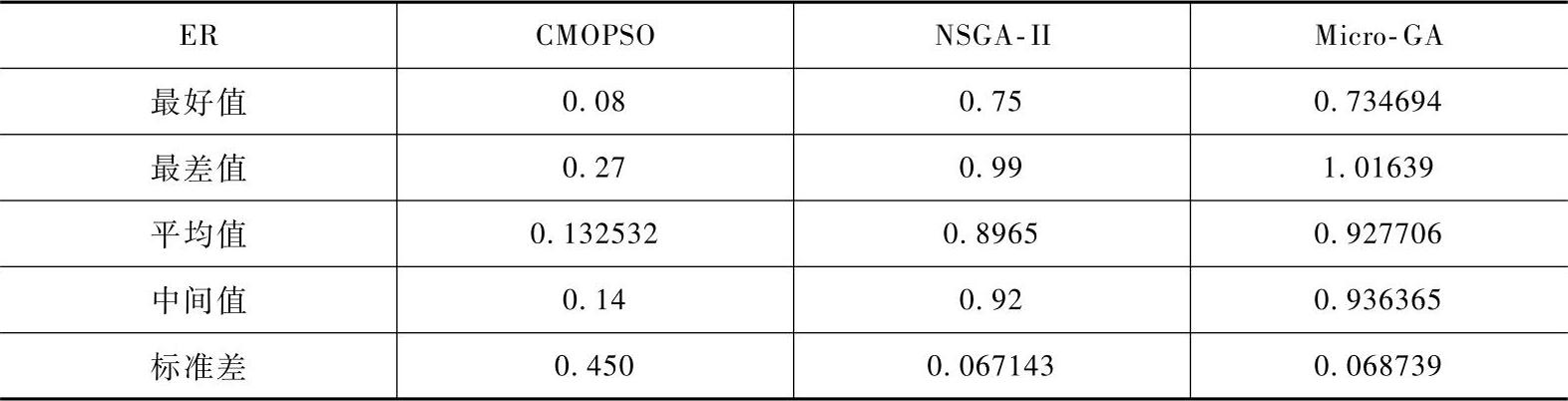
表2-5 三种算法关于测试函数所得的GD值

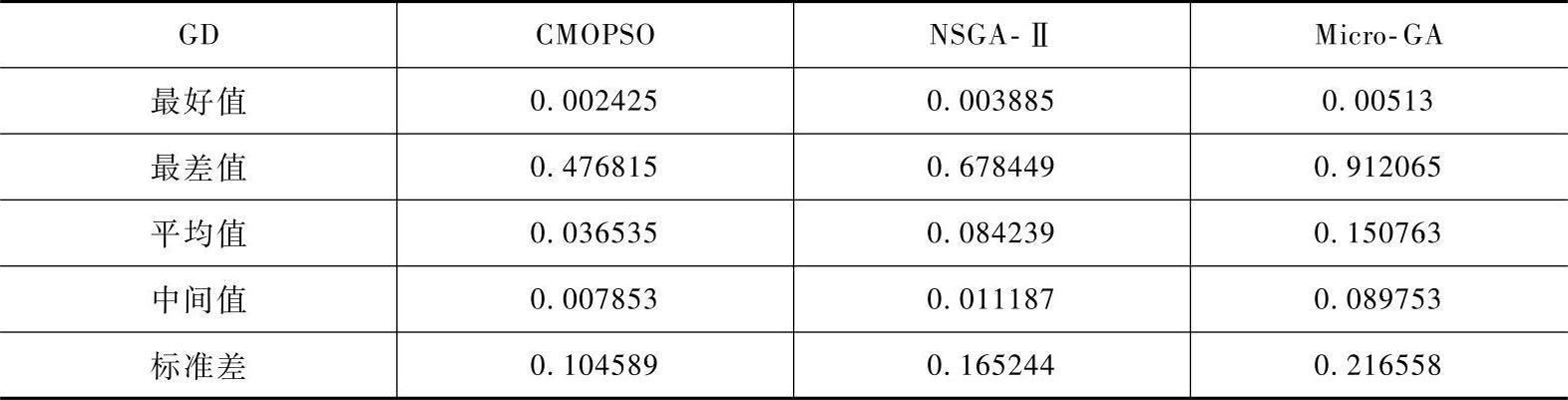
表2-6 三种算法关于测试函数所得的SP值

2.细胞遗传算法（MOCell）

2009年，Nebro等^[107]学者提出一种针对多目标优化问题的细胞遗传算法——MOCell。此后的研究表明：在求解众多函数优化问题中，MOCell在收敛性和均匀性方面都表现出色，是近年来优秀的进化多目标优化算法。文献[107]中提出，MOCell通过采用外部种群存储非劣种群，并通过一种反馈机制在每次迭代后从种群个体中随机抽取非支配个体替换当前个体。

（1）基本的细胞遗传算法 在介绍MOCell之前先介绍基本的细胞遗传算法（CGA），其伪代码见表2-7。在基本细胞遗传算法中，种群个体和邻代个体通常存在于d（d=1，2，3）维的规则网格中。算法在运行过程中种群个体都存在于网格之中（表2-7第3行）。种群个体可能只和其邻代个体（表2-7第4行）进行信息交流，因此当前个体只能在父代个体和其邻代个体中进行选择（表2-7第5行）。表2-7第6行和第7行分别表示交叉和变异操作，之后算法将计算子代适应度值（表2-7第8行）。按照给定的替换规则，将子代个体（或它们中的一个）插入新种群（表2-7第9行）中当前个体的同样位置。将这种生成规则应用到种群中每个个体后，新产生的额外种群即下一代（表2-7第11行）的新种群。这种循环会一直进行下去，直到满足算法终止条件（表2-7第2行）。

表2-7 典型细胞遗传算法(www.xing528.com)

（2）MOCell算法MOCell算法是基于cGA模型的进化多目标优化算法，其伪代码见表2-8。值得注意的是，表2-7和表2-8非常相似，它们之间主要的不同之处在于在多目标优化中存在Pareto前沿。为了使种群个体的生成多样化，MOCell采用基于拥挤距离的个体密度估计方法。

表2-8 MOCell算法

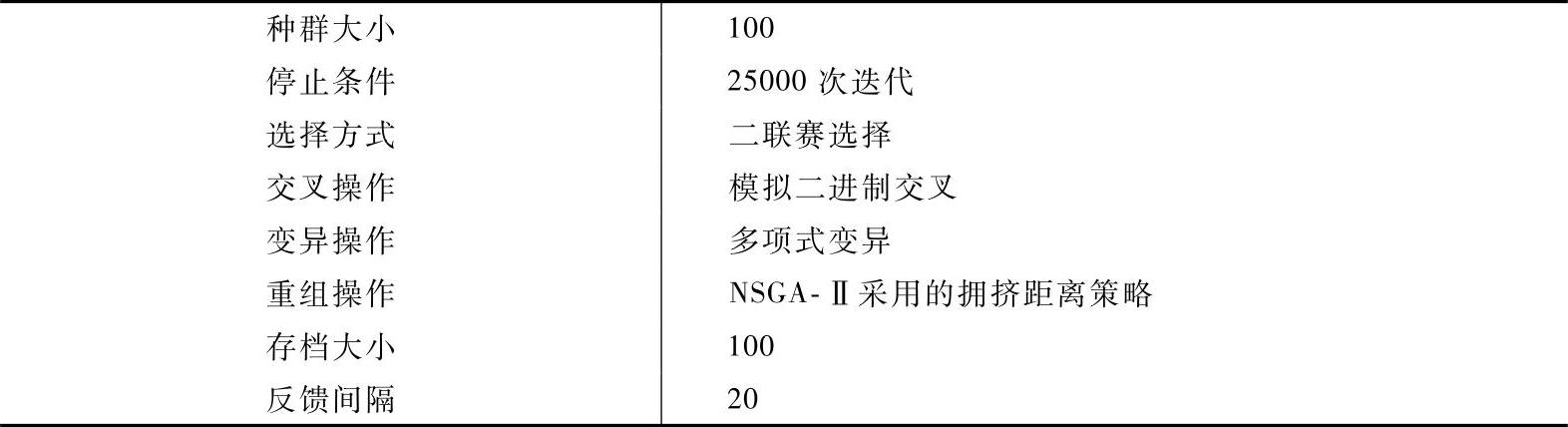
（3）MOCell实验结果 为了对MOCell算法性能进行测试，本小节将选取经典的进化算法NSGA-II和SPEA2与之进行比较。采用的测试函数包括不带约束测试函数和带约束测试函数。不带约束测试函数包括Schaffer、Fonseca、Kursawe、ZDT1～ZDT4和ZDT6，带约束测试函数包括Osyczka2、Tanaka、ConstrEX和Srini-vas。由于使用函数都为常用测试函数，本文不一一给出，详见文献^[107]。表2-9为MOCell参数设置。

表2-9 MOCell参数设置

本文将对MOCell、NSGA-Ⅱ和SPEA2采用GD指标进行评价。表2-10为三个算法收敛性指标GD的均值和方差。

表2-10 三个算法收敛性指标GD的均值和方差

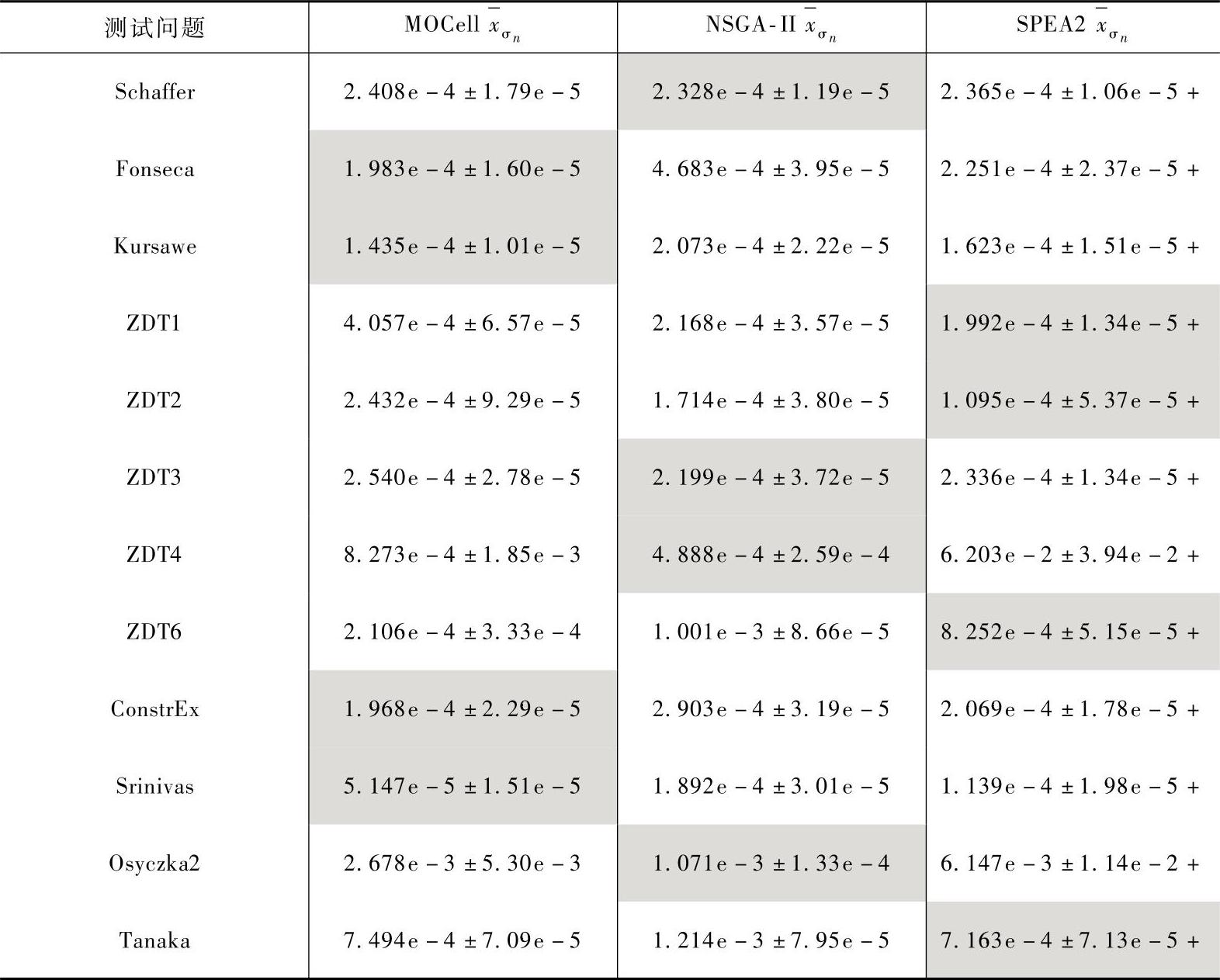
表2-10中，将每个测试问题的最优结果用灰色标出。对于每一个测试问题，都进行了100次独立运行。我们采用随机算法对结果进行统计分析，这个过程包括以下几个步骤：首先，为了检查结果是否遵循正态分布，采用Kolmogorov-Smirnov进行测试。如果是正态分布就再进行ANOVA I测试，否则进行Kruskal-Wallis测试。在这个步骤中，一般是采用统计分析中95%作为置信区间。在表2-10中符号“+”表示对于一个给定的问题，三种算法值的偏差具有统计置信度（在0.05下的p值）。

通过观察表2-10可知，在所研究的12个测试问题中MOCell有4个问题提供了最优结果。根据测试结果表明，MOCell比NSGA-II和SPEA2在某些测试问题上存在优势但并不能确定哪种算法更好，但通过与经典的进化算法在函数优化问题的比较，可以发现MOCell是一种比较优秀的进化算法。

3.快速Pareto遗传算法（FastPGA）

2007年，Eskandari等^[108]学者提出了快速Pareto遗传算法（FastPGA）。FastP-GA采用了新的适应度赋值、分等级策略、种群调控操作算子和精英操作算子。精英操作算子的实施能够保证Pareto最优解集的快速收敛。而种群调控操作算子通过引入动态自适应种群规模，可以修改种群最大规模，它的实施可以加快算法的收敛速度和降低计算复杂度。快速Pareto遗传算法框架实际上是一种基于种群的实数编码的进化算法。一般来说，采用实数编码的多目标遗传算法能够有效避免二进制编码与位操作所带来的麻烦，尤其在处理高维连续搜索空间中优势更为明显。其算法伪代码见表2-11。

表2-11 快速Pareto遗传算法

（1）FastPGA算法流程FastPGA算法主要步骤如下：

1）初始化所有决策参数。

2）在第1代进化中，采用随机方式初始化候选解向量种群P_t。

3）如果是第1次进化，跳转到步骤5）；否则，进化代数加1并采用规模为2的联赛选择方式从父代P_t-1中选择新的子代P_t-1。

4）执行交叉、变异操作，生成新的候选解（子代）Q_t。

5）计算m维目标函数的候选解向量并将其保存。

6）将生成的候选解Q_t和父代种群P_t-1结合，生成新的种群CP_t。

7）通过利用它们的适应值，采用新的分等级策略对新种群CP_t进行分等级。

8）根据非支配解的数量调节种群规模，剔除合成种群CP_t中非劣解生成新的种群P_t。

9）如果满足终止条件立即终止，否则跳转到步骤3）。

（2）新的分等级策略和适应度赋值 新的分等级策略是基于复合种群CP_t中候选解分类，按照解的支配关系分为两个不同的等级。所有非支配解被确定为第一等级，即在考虑所有目标的情况下，不存在比这些非支配解更好的解；所有被支配解被确定为第二等级。在种群繁殖过程中，这些等级被用来评价个体的适应值。

第一等级的个体适应值是通过比较每个非支配解与同等级其他解进行分配。这些适应值采用Deb在NSGA-II中提出的拥挤距离方法得到，这个方法能够保证Pa-reto最优前沿中非支配解的多样性。

第二等级解的适应值通过将每个解与同等级其他解进行比较，然后依据被其支配的解的个数分配适应值。这与SPEA2采用方式相似但对其进行了改进。更确切地说，每一个被支配的解x_i在分配适应值同时考虑了被该解支配的解和支配该解的解。复合种群CP_t中的每一个解x_i都分配强度值S（x_i），用来表示它所支配的解个数，其中：

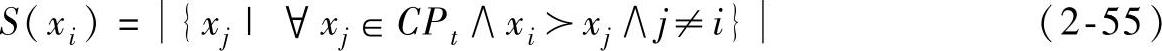
用|·|表示一组基数解集，表达式x_i＞x_i表示解x_i支配解x_i。每一个被支配解的适应值即其强度值，可通过式（2-56）求得。

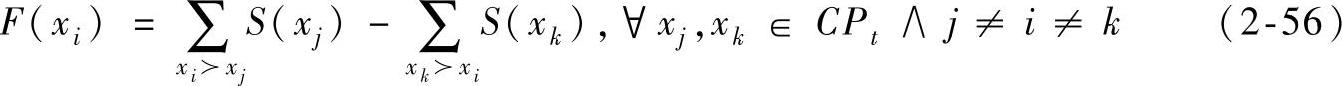
在FastPGA中，每一个被支配个体x_i的适应值等于它支配的所有解强度值之和减去支配它的解的强度值之和。而在SPEA和SPEA2中，x_i的强度值仅由支配它的解决定。该策略能够为复合种群的解提供更多的关于Pareto支配关系和小生镜的信息，并且能够减小两个解出现相同适应值的概率。因此，在第二等级的被支配解上没有额外的多样性保护机制，使得计算量大大减小（而在SPEA2中密度估计方面需要花费很多的计算时间）。

（3）精英策略和种群调控 采用适当高强度的精英操作可以确保非支配解遗传给下一代，该操作通过复制当前种群P_t-1中的所有解到复合种群CP_t中实现。将种群P_t-1和子代种群0_t合并时，可以将优秀的解保存下来，同时依据复合种群中获得的非支配解的数目将劣等解丢弃。

随着进化代数的增加，非支配解的数目也会增加。如果种群规模很大且保持不变，在早期的种群进化中将导致低的精英强度保留。此外，后代中非支配解的数目需要一个自适应的控制种群规模的机制，来适当控制一些非支配解的精英强度。如果精英强度过高，可能会出现早熟收敛；如果精英强度很低，收敛太慢且计算量太大。因此，FastPGA采用了一种动态方式调整种群规模，直到达到用户规定的最大种群数量，见式（2-57）。

|P_t|=min{a_t+[b_t×|{x_i|x_i∈CP_t∧x_i非支配}|]，maxpopsize} （2-57）式中，|P_t|是第t代种群规模；a_t是一个正整数变量，随着代数增加而变化；bt是一个正实数变量，可能随代数增加变化；[x]表示大于或者等于实数x的最小整数；maxpopsize是用户规定的最大种群规模。

FastPGA产生少量的子代进行交叉和变异操作。子代产生的数目由式（2-58）计算得出。

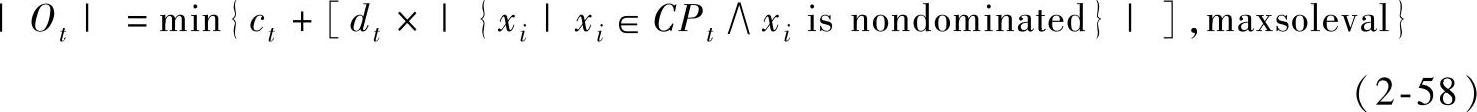
式中，|Q_t|是第t代产生的子代数目；c_t是一个正整数变量，可能随代数的增加而变化；d_t是一个正实数变量，可能随代数的增加而变化；maxsoleval是用户定义的每代中评估解的最大数量。

在文献[108]中，作者将FastPGA与NSGA-II在函数优化问题上进行比较，实验结果表明：FastPGA在收敛性和均匀性上都比NSGA-II优秀。