基于南京新街口中心区80组声环境参数及指标因子，用最小二乘法做行人高度处平均声压级与建筑密度、围合度、建筑尺度原始数据的多元线性回归，得到回归方程：
式中：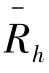
=1.6为行人高度处平均声压级；X为建筑密度；Y为围合度；Z为建筑尺度。
由于行人高度处平均声压级与建筑密度、围合度、建筑尺度原始数据的数量级和单位存在差异，上式中的各指标的回归系数难以反映影响程度的差异，因此本书将各组数据进行标准化处理，将其转化为无量纲的纯数值，便于各指标能够进行比较。本书数据标准化采用离差标准化方法，对原始数据进行线性变换，使结果映射到［0，100］区间，其计算公式如下：
其中，
为该数据集中的最大值，
为该数据集中的最小值，则标准化的数据y1，y2，…，yn∈［0，100］。
将80组数据按照离差标准化方法标准化后，再利用最小二乘法做多元线性回归，得到回归方程：
式中：
为标准化后的行人高度处街区平均声压级；X*为标准化后的建筑密度；Y*为标准化后的建筑尺度；Z*为标准化后的围合度。
该回归方程的判定系数R2为0.510，说明样本的回归效果一般；F检验的统计量F=26.399，相伴概率值P＜0.001，说明三个自变量与因变量存在线性回归关系；各自变量t检验的相伴概率值P均小于0.05（建筑密度标准化P=0.002，建筑尺度P＜0.001，围合度P=0.001），说明各自变量与因变量都存在显著的线性关系。
多元线性回归效果一般，主要可能存在以下的原因：（1）本节所用的80个街区的行人高度处街区平均声压级参数是结合南京新街口中心区实际的道路交通数据模拟分析得到的结果，每个区块的声环境会受到外部不同类型等级的道路交通的影响，因此并不是区块内部建筑空间单一的影响结果；（2）本节仅对建筑密度、围合度、建筑尺度三项存在明显线性相关的指标因子做了多元线性回归分析，还有部分指标未纳入考虑，同时区块单元的建筑布局、组合方式对行人高度处的街区声环境也存在较大影响，但这类影响因素难以进行指标量化的描述。(www.xing528.com)
但通过多元线性回归分析，可以进一步确定行人高度处的平均声压级与建筑密度、建筑尺度、围合度存在显著的线性关系，其中，与建筑密度、围合度成负相关关系，与建筑尺度成正相关关系。并且，从数据标准化后所得的回归方程（2）中可以看出三个指标因子的影响程度依次应为建筑尺度＞围合度＞建筑密度。
【注释】
[1]环境保护部，国家质量监督检验检疫总局.声环境质量标准［S］，2008.
[2]DataKustik.Calculation Standards.http：//www.datakustik.com/en/products/cadnaa/modeling-andcalculation-standards/，2010
[3]环境保护部，国家质量监督检验检疫总局.声环境质量标准［S］，2008
[4]具体检验方法可参考：王松桂，陈敏，陈萍，等.线性统计模型：线性回归与方差分析［M］.北京：高等教育出版社，1999.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
