工程制图与识图：轴测投影

轴测图是用轴测投影方法绘制出的富有立体感的图样，在实际工程中常作为辅助图样，帮助空间想象，建立空间概念、构思分析和辅助读图。本节主要介绍轴测图的图示特点和作图方法。

3.1.1 轴测投影图的形成与分类

1. 轴测投影图的形成

多面正投影图表达空间物体具有画图简单，投影形状真实、度量方便等优点，因此在实际工程中被广泛应用。但多面正投影图的投射方向总与物体的某一主要方向一致，使得每一个视图，只能表达物体一个方面的尺度和形状，且缺乏立体感，不够直观，读懂这类图需要具备专业的读图知识。如果用平行投影的方法，将物体连同其坐标轴一同向一个投影面进行投影，利用三个坐标轴确定物体的三个尺度，就能在一个投影面中得到反映物体长，宽、高三个方面的形状和尺度的图形，这种投影方法，称为轴测投影法。用轴测投影法所得到的图形，称为轴测投影图 (简称轴测图或立体图)，如图3-1所示。

轴测投影图的优点是比较直观和立体感强，能较清楚地表达物体的形象，容易看懂，因而在实际工程中也有较多应用，如辅助读图、外观设计等。其缺点是度量性较差，不能完全反映物体的真实形状和大小，且作图麻烦。实际工程中有时用轴测图作为辅助图，以表达物体的立体关系和位置。

如图3-1所示，为空间立方体的轴测投影图，该图是将立方体连同其直角坐标系，沿不平行于任一坐标面的方向，用平行投影法将其投射在单一投影面P上所得到的图形。由图3-1可以看出，该图反映了立方体三个尺度。图3-1中P为轴测投影面，ox、oy、oz为空间直角坐标系的三个坐标轴，O1x1、O1y1、O1z1为相应三个坐标轴在轴测投影面上的投影。

图3-1 立方体的轴测投影图

空间直角坐标轴Ox、Oy、Oz在轴测投影面上的投影O1x1、O1y1、O1z1称为轴测投影轴，简称轴测轴。每两根轴测轴之间的夹角∠x1O1y1、∠x1O1z1、∠z1O1y1称为轴间角。

空间某线段沿某轴测轴的投影长与其沿相应空间坐标轴的实际长度之比，称为该轴的轴向变形系数，即

轴间角和轴向变形系数是绘制轴测图的两个重要参数，种类不同的轴测图其轴间角和轴向变形系数各不相同。

由于轴测投影是用平行投影方法进行的投影，所以轴测投影具有平行投影的特性：

(1) 空间直线，其轴测投影仍然为直线；

(2) 空间相互平行的直线，其轴测投影仍然相互平行；

(3) 空间上平行于坐标轴Ox、Oy、Oz的线段，即轴向线段，其轴测投影也必然与相应的轴测轴平行，并且所有同轴的轴向线段，其变形系数相同。

由多面正投影图绘制轴测图时，物体上与轴向平行的线段，在多面正投影图中可以直接量取实际尺寸后，乘以相应的轴向变形系数即得其轴测投影长度，这就是“轴测”二字的含义，亦即沿轴的方向可以测量尺寸。而与轴向不平行的线段，不能在轴测图中直接作出，只能通过坐标定点的方法作出其两个端点后连线得到该线段。

2. 轴测投影图的分类

随着投射方向、空间物体和轴测投影面三者相对位置的变化，可以得到无数轴测图。根据投影线方向和投影面的关系，轴测投影图分为以下两类：

(1) 正轴测图。使投影线与轴测投影面垂直所得到的轴测图称为正轴测投影图，也称为直角轴测投影。如图3-1 (a) 所示，使确定物体位置的三个坐标轴Ox、Oy、Oz都与投影面P斜交，然后用正投影法将物体连同坐标系一起投射到P投影面上，即得到该物体的正轴测图。

(2) 斜轴测图。使投影线与轴测投影面斜交所得到的轴测图称为斜轴测投影图，也称为斜角轴测投影图。如图3-1 (b) 所示，使反映物体长和高的一面 (即坐标面x Oz)平行于投影面P，然后用斜投影法将物体连同坐标系一起投射到P投影面上，即得到该物体的斜轴测图。根据需要，在轴测投影中也可以使反映物体长和宽的一面 (即坐标面x Oy) 或宽和高的一面 (即坐标面y Oz) 平行于投影面P。

根据轴向变形系数的不同，上述每种轴测投影图又可以分为三种：

1) 当p=q=r时，称为正 (或斜) 等测投影图；

2) 当p=q≠r或p≠q=r或p=r≠q时，称为正 (或斜) 二测投影；

3) 当p≠q≠r时，称为正 (或斜) 三测投影。

实际工程中常用的是正等测图和斜二测图。本章主要介绍正等测图和斜二测图的画法。

3.1.2 正等测图

1. 正等测图的形成

正等测图是用正轴测投影的方法并使其三个轴向变形系数相等作出的轴测投影图。

绘制正等测图，首先作三根互成120°的轴测轴O1x1、O1y1、O1z1，一般使O1z1与水平线成直角(铅垂方向)，O1x1、O1y1与水平线成30°角，如图3-2所示。

图3-2 正等测图的轴间角

三个轴间角相等，即∠x1O1y1=∠x1O1z1=∠z1O1y1=120°； 三个轴向变形系数p、q、r相等，p=q=r=0.816。为了绘图方便，一般把三个轴向变形系数均取为1，即p=q=r=1。画图时，凡平行于各坐标轴的线段，可以按其实际长度量取，虽然作图结果放大了约1.22倍，但物体形状没有改变。

2. 平面体正等测图的画法

一般地，根据物体的正投影图绘制轴测图的基本步骤为：

(1) 识读多面正投影图，通过形体分析看懂物体，并确定原点和参考坐标系的位置。

(2) 确定轴测图种类，作出轴测轴，根据物体的特点，选取适当的方法完成轴测图。轴测图上只绘制可见部分的轮廓线，不可见部分的虚线一般不绘制。因此，作图时经常先从物体上的某一可见表面开始，在完成每一个表面时，先绘制和轴平行的线段，再绘制和轴不平行的线段。

(3) 检查加深。确定作图结果后，擦去作图线，加深物体上所有可见轮廓线。

绘制轴测图的作图方法常有坐标法、特征面法、叠加法和切割法等。其中坐标法是最基本的方法，其他方法都是根据物体的特点对坐标法的灵活应用。

作比较复杂的物体的轴测图时，常将几种方法综合应用。下面举例说明各种作图方法的运用。

1) 坐标法。首先引入参考直角坐标系，确定物体上相对于坐标系的坐标，然后绘制出相应的轴测轴，根据物体上各特征点的坐标，沿轴测轴方向进行度量，绘制出各点的轴测投影，最后依次连接各点，即可得到该物体的轴测图。

【例3-1】如图3-3所示，为三棱锥的两面投影图，试作其正等测图。

分析： 设三棱锥的坐标系为O1X1Y1Z1，则可以确定三棱锥上各点S、A、B、C的坐标值。

为方便作图，使X1O1Y1坐标面与锥底面重合，O1X1轴通过点B，O1Y1轴通过点C，如图3-3 (a) 所示。

图3-3 坐标法绘制三棱锥正等测图

作图： 如图3-3 (b) 所示，绘制出正等测的轴测轴，按坐标值沿轴向量取尺寸，由此确定各点的位置。连接点S、A、B、C，并描深可见的棱线和底边，结果如图3-3 (c)所示。

2) 特征面法。特征面法适用于绘制柱类物体的轴测图。通常是先绘制出反映柱体特征的一个可见端面，再绘制出可见的棱线和另一端面的可见边线，完成物体的轴测图。这种方法称为特征面法。

【例3-2】如图3-4 (a) 所示，为正六棱柱的两面投影，试作其正等测图。

分析： 该正六棱柱前后、左右对称，为了便于作图，选取顶面中心点为坐标原点，以顶面六边形的中心线为O1X1轴和O1Y1轴，如图3-4 (a) 所示。从可见的顶面开始作图。

作图： 绘制出正等测的轴测轴，作正六棱柱的顶面，顶点1、3在OX轴上，点2、4在OY轴上，直接量取可得，分别过点2、4作OX轴的平行线，量取顶面上前后两个边的长度，可得5、6、7、8四个顶点，依次连线绘制出顶面的正等测图，如图3-4 (b) 所示。过顶面各顶点沿OZ轴方向绘制出相平行的可见棱线，在棱线上截取棱柱的高度，得底面各点，如图3-4 (c) 所示。擦去作图线，描深可见图线。结果如图3-4 (d) 所示。

图3-4 特征面法绘制正六棱柱的正等测图

3) 叠加法。绘制由几部分叠加而成的物体的轴测图时，应该从主到次逐个绘制出各基本体的轴测图，作图时确定各部分之间的相对位置是关键。

【例3-3】如图3-5 (a) 所示，为挡土墙的两面投影，试完成其正等测图。

分析： 该挡土墙可以看成由一个正垂“⊥”形棱柱和前后对称的两个三棱柱叠加而成。先绘制主体“⊥”形棱柱，再逐一将两个三棱柱绘制出，完成作图。

作图： 绘制出正等测的轴测轴，用特征面法绘制“⊥”形棱柱，如图3-5 (b) 所示；根据尺寸Y1准确定位，以点A为起画点，用特征面法绘制前方三棱柱，如图3-5 (c) 所示； 根据尺寸Y2准确定位，以点B为起画点，用特征面法绘制后方三棱柱，如图3-5 (d)所示； 擦去被遮挡的图线，检查加深完成作图。结果如图3-5 (e) 所示。

4) 切割法。对于能从基本体切割而成的物体，可以先绘制出原体的轴测图，然后分步进行切割，切割时一定要注意切割位置的确定。

【例3-4】如图3-6 (a) 所示为物体的三面投影，试作其正等测图。

图3-5 叠加法绘制挡土墙的正等测图

分析： 该物体可以看成是“L”形棱柱被切割两次，右前上方切掉一个四棱柱，左前方切掉一个三棱柱。

绘制轴测图时，可以先绘制出完整的“L”形棱柱，再逐次进行切割。

作图： 绘制出正等测的轴测轴，用特征面法绘制出“L”形棱柱，如图3-6 (b) 所示； 由投影图量取准确位置，切掉右前上方的小四棱柱，如图3-6 (c) 所示； 量取准确位置，切去左前方三棱柱，如图3-6 (d) 所示； 最后擦去作图线，描深可见图线。结果如图3-6 (e) 所示。

5) 观察方向的选择。对同一种轴测图，为了把物体表达得更清楚，可以根据物体的形状特征选择适当的观看方向，如俯视、仰视、从左看、从右看等。

如图3-7所示，为物体从不同方向观察得到的正等测的不同效果，其中图3-7 (a) 为从左侧观看的俯视图，图3-7 (b) 为从右侧观看的俯视图，图3-7 (c) 为从左侧观看的仰视图，图3-7 (d) 为从右侧观看的仰视图。对于本例，图3-7 (c) 最能表现物体各部分的形状，效果最好。

3. 曲面体正等测图的画法(www.xing528.com)

曲面体正等测图的画法与平面体相同。绘制曲面体正等测图的关键是掌握物体上圆和圆弧的画法。

(1) 平行于坐标面的圆的正等测图画法。当圆所在的平面平行于轴测投影面时，其投影仍为圆； 当圆所在的平面倾斜于轴测投影面时，其投影为椭圆。一般情况下，圆柱、圆锥和圆台等的端面圆都平行于某个坐标面，正等轴测投影中，各坐标面都倾斜于轴测投影面且倾角相同，所以平行于不同坐标面的圆其正等测图都是椭圆，如图3-8所示，从图3-8中可以看出：

图3-6 切割法绘制物体的正等测图

图3-7 选择观察方向

1) 圆的中心线的正等测图平行于相应坐标面上的两个轴测轴。若水平圆平行于X1O1Y1坐标面，其中心线的正等测图平行于OX、OY两个轴测轴； 正平圆平行于X1O1Z1坐标面，其中心线的正等测图平行于OX、OZ两个轴测轴； 侧平圆平行于Y1O1Z1坐标面，其中心线的正等测图平行于OY、OZ两个轴测轴。

图3-8 平行于坐标面的圆的正等测图

2) 椭圆的长轴方向垂直于相应坐标面之外的轴测轴。若水平圆的正等测图，其长轴垂直于OZ轴； 正平圆的正等测图，其长轴垂直于OY轴； 侧平圆的正等测图，其长轴垂直于OX轴。

平行于坐标面的圆的正等测图，常用菱形四心法绘制，即用四段圆弧光滑连接，近似绘制出椭圆，这种方法仅适用于正等测图。下面以作水平圆的正等测为例，具体画法如图3-9所示，其步骤为：

①定原点和坐标轴，作圆外切正方形，得4个切点a、b、c、d，如图3-9 (a) 所示。

②作轴测轴和四个切点A、B、C、D，过这4点分别作OX、OY轴的平行线，得圆的外切正方形的正等测菱形，如图3-9 (b) 所示。

③分别过这4个切点A、B、C、D作各自所在边的垂线，得4个交点1、2、3、4，即为4段圆弧的圆心，其中3、4为菱形短对角线的端点，如图3-9 (c) 所示。

④分别以1、2为圆心，1B为半径作圆弧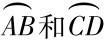，再分别以3、4为圆心，4B为半径作圆弧，4段圆弧光滑地连成椭圆，如图3-9 (d) 所示。

图3-9 菱形四心法绘制水平圆的正等测图

(2) 曲面体正等测画法。

【例3-5】如图3-10 (a) 所示，为铅垂圆柱的两面投影，试绘制其正等测图。

分析： 该圆柱轴线为铅垂线，顶面圆和底面圆分别位于X1O1Y1坐标面及其平行面上，其正等测为形状、大小相同的两个椭圆，以菱形四心法作图，然后绘制两椭圆的公切线即可。

作图： 以顶面圆心为坐标原点，设定坐标轴，并作顶面圆的外切正方形，切点为、a、b、c、d，如图3-10 (a) 所示。

按照图3-9的步骤用菱形四心法绘制出顶面圆的正等测图，如图3-10 (b) 所示。

图3-10 作铅垂圆柱的正等测图

为了减少作图，底面圆的正等测图只需绘制三段可见的圆弧，为此，用移心法将顶圆圆心O、圆弧圆心1、2、3和4个切点A、B、C、D均沿OZ轴下移圆柱的高度，然后用相应的半径绘制出底圆圆弧，得底圆的正等测图，如图3-10 (c) 所示。

绘制两椭圆的公切线，擦去作图线，描深可见轮廓线，完成作图，结果如图3-10 (d) 所示。

正垂圆柱和侧垂圆柱的正等测图的画法与铅垂圆柱正等测图的画法相同。绘制圆锥的正等测图时，先绘制底面圆的正等测图，再定锥顶，最后由锥顶向底面圆作公切线。圆台的正等测图与圆柱基本相同，分别绘制出两端面圆的正等测图，再作它们的公切线，如图3-11所示。

【例3-6】如图2-12所示，为曲面体的两面投影，试绘制其正等测图。

分析： 该曲面体由底板和立板两部分组成。底板前方左右两角为1/4圆角，需要绘制1/4圆的正等测图。带有圆柱通孔的立板上部为半圆柱体，需要作1/2圆的正等测图。画图时综合运用前述方法。

图3-11 曲面体的正等测图实例

作图：

(1) 作底板的正等测图。画底板的圆角时，从底板顶面左右两角点沿顶面的两边量取圆角半径，得切点1、2、3、4，过切点作边线的垂线，交得圆心O1、O2，以圆心到切点的距离为半径画弧，即为圆角正等测图，用移心法画底面圆角，注意作出右前角处的公切线，如图3-12 (b) 所示。

图3-12 曲面体正等测图的画法

(2) 作立板的正等测图。立板由四棱柱和半圆柱组成，绘制半圆柱的正等测图时，作出前端面上1/2圆的外切正方形的正等测图，过切点作边线的垂线，交得圆心O3、O4，以圆心到切点的距离为半径画弧，用移心法画后端面上的半圆，注意作出公切线，如图3-12 (c) 所示。

(3) 作立板上圆柱的正等测图。圆柱通孔后孔口的轮廓线是否可见取决于板厚，如图3-12 (d) 所示。

(4) 擦去作图线，描深可见轮廓线，完成作图，结果如图3-12 (e) 所示。

3.1.3 斜二测图

1. 正面斜二轴测图

斜二测图是用斜测投影的方法，并使其两个轴向变形系数相等作出的轴测投影图。为了作图方便和作出的轴测图立体感强，一般采用p=r=1，q=0.5，轴向角∠XOZ =90°，∠YOZ = 135°，Y轴与水平线成45°。方向可以选向右下、左下、右上、左上等，如图3-13所示。这样得到的正面斜轴测图称为正面斜二轴测图，简称正面斜二测。由于物体上的正立面反映实形，所以这种图适用于画正面形状复杂、曲线多的物体。

图3-13 正面斜二测图的轴间角和轴向变形系数

(1) 平面体的正面斜二测图。平面体的正面斜二测图的画法与正等测图画法基本相同，区别只是两者的轴间角和轴向伸缩数不同。

【例3-7】试绘制图3-14 (a) 所示物体的正面斜二测图。

分析： 该物体由台阶和栏板前后叠加而成，用叠加法完成作图。台阶和栏板前端面的正面斜二测均反映实形，各自用特征面法作图。

作图： 绘制正面斜二测的轴测轴，绘制出台阶前端面的实形，从前端面的各顶点向后拉伸出OY方向的平行线，按q=0.5确定台阶宽度，如图3-14 (b) 所示； 确定位置，用同样的方法绘制出栏板，如图3-14 (c) 所示； 擦去作图线，加深可见轮廓线，完成全图，结果如图3-14 (d) 所示。

(2) 曲面体的正面斜二测图。曲面体的正面斜二测图的画法与正等测图画法基本相同，只是物体上平行于坐标面的圆的画法不同。

图3-14 台阶的正面斜二测图

1) 平行于坐标面的圆的正面斜二测图。正面斜二测图中，平行于坐标面X1O1Z1的圆(正平圆)，其正面斜二测图反映实形，可以直接绘制出，如图3-15所示； 平行于坐标面XlOlYl和Y1O1Zl的圆(水平圆和侧平圆)，其正面斜二测图是椭圆，常用八点法或描点法绘制图。

八点法作图适用于绘制任意位置圆的各类轴测图。

以水平圆为例，具体画法如图3-15所示，作出圆的外切正方形的正面斜二测图，得一平行四边形，然后以轴向伸缩系数为1的半条边为斜边作等腰直角三角形，将作得的直角边的长度量在这条边中点的两侧，由量得的点作OY轴的平行线，与平行四边形的对角线交得四个点，再连同平行四边形的四个中点一起，由八个点连成椭圆。

图3-15 平行于坐标面的圆的正面斜二测图

描点法是通过平行于坐标轴的弦，作出圆周上若干点的轴测图，再光滑连成椭圆，如图3-15中侧平圆的正面斜二测图所示。

2) 曲面体的正面斜二测画法。

【例3-8】试绘制图3-16 (a) 所示物体的正面斜二测图。

分析： 该物体由同轴的大、小两个圆柱叠加而成，用叠加法完成作图。由于大、小两圆柱的前后端面都是正平圆，其正面斜二测图反映实形。

作图： 作出轴测轴，先绘制小圆柱的轴测图，注意作前后端面圆的公切线，如图3-16 (b) 所示； 准确定位，绘制大圆柱的轴测图，如图3-16 (c) 所示； 擦去作图线，加深可见轮廓线，完成全图，结果如图3-16 (d) 所示。

图3-16 平行于坐标面的圆的正面斜二测图

2. 水平斜二轴测图

使空间物体的X1O1Y1坐标面(即物体上的水平面) 平行于轴测投影面，所得到的斜轴测图称为水平斜轴测图。

由于坐标面X1O1Y1平行于投影面，故轴间角∠XOY=90°，轴向变形系数p=q=1。OZ轴及其轴向变形系数随着投射线方向的改变而变化，可以任意选择，为作图方便，OZ轴绘制成竖直方向，取r=0.5，OX和OY分别与水平线成30°和60°，这样得到的水平斜轴测图称为水平斜二轴测图，简称水平斜二测图，如图3-17所示。水平斜二测图在实际工程中常用于绘制建筑群的鸟瞰图。

水平斜二测图的轴间角和轴向变形系数

【例3-9】试绘制出如图3-18 (a) 所示建筑物体的水平斜二测图。

作图： 作出轴测轴，将图3-18 (a) 中的水平投影逆时针旋转30°后绘制出，如图3-18 (b)所示； 再在各转角处沿OZ轴方向画线，按照r=0.5量取高度，最后绘制出各部分的顶面。

完成后的水平斜二测图，如图3-18 (c) 所示。

图3-18 建筑物体的水平斜二测图