锂电池模型：现代车辆新能源技术

建模的意义在于确定锂电池所处环境因素与其特征量之间的数学关系，考虑的对象包括电动势、端电压、工作电流、温度、内阻、SOC及SOH等，找到它们之间的联系对电池管理系统的开发具有重要意义。一方面，通过所建立的锂电池模型可对锂电池在工作中的各种表现进行估计，从而对各种电池管理策略（如能量控制策略、电池均衡策略等）进行仿真。可通过软件法快速检验策略的有效性，这不仅节约了硬件成本，还缩短了验证周期，节约了开发时间。另一方面，精确的锂电池模型对SOC评估算法具有重要意义。建立较为精确的外特性模型，对寻找SOC与各种可直接测量的物理量之间的数值联系极为有利，进而可通过监测到的外部表现来评估内在的SOC。

本节所讨论的锂电池模型属于外特性模型。从本质上看，就是要解决锂电池的伏安特性关系，即能描述锂电池在工作过程中所表现出的电压与电流之间的关系。这种关系一方面可利用数值关系表达，另一方面可把锂电池视作一个二端口的网络，而用一个电路网络来反映其伏安关系。从这个意义上说，可通过建立一个等效电路来描述动力电池在工作过程中的伏安关系。这种电路遵循戴维南（Thevenin）定律，因此有时也被称作Thevenin模型。以下列举几种具有代表性的等效电路模型。

1）基于电子运动理论的等效电路模型（图7-2-12）。根据锂电池内阻和双电层理论，较好地描述了锂电池的特点，但忽略了锂电池在工作过程中两个电极所表现出的不同电位差（两个电极偏离平衡电位的程度不同）。该等效电路不能很好地表现出锂电池的回弹电压特性。

图7-2-12中，R_f与C_d构成的两个RC回路代表锂电池的两个电极系统。R_Ω代表锂电池本身存在的欧姆电压降。

2）PNGV等效电路模型（图7-2-13）。PNGV模型是《FreedomCAR电池试验手册》中的标准电池性能模型。该电路模型虽然包括了电极的极化，电池的欧姆电阻等特性，但仍没有体现锂电池的电压回弹特性。此外，PNGV模型中的每个参数都会随锂电池的SOC和温度的改变而改变，模型参数的辨识较复杂，不适合实时的SOC估算，实用性不强。

图7-2-12 基于电子运动理论的电池等效电路

R_f—电池的极化内阻 R_Ω—电池的欧姆电阻 C_d—双电层电容

图7-2-13 PNGV等效电路模型(www.xing528.com)

R_f—电池的极化内阻 R_Ω—电池的欧姆电阻 C_d—双电层等效电容 C_o—开路电压随负载电流的时间累计而产生的变化

3）带有滞回特性的电路模型（图7-2-14）。该模型在阻容等效电路模型的基础上考虑了锂电池平衡电势，即用V_h表示锂电池的滞回电压，并作为锂电池平衡电势的一部分。但对于韦伯阻抗参数值的求解，需要用到锂电池的内阻谱，而内阻谱的测定需要用特定电化学测量法。该测量法所需仪器较难获得，这就对模型的建立造成了一定的影响。另外，该模型尽管考虑了锂电池滞回电压的影响，但没有直接反映出锂电池SOC，需要分析计算后才能得到。综上所述，现有的几种常用锂电池模型存在以下不足：

电压源与SOC之间的关系不够明确。

有些模型过于简单，不能很好地描述锂电池的动态特性，如电压回弹特性。

某些模型未能反映某些锂电池的滞回效应。

因此，在针对锂电池建模前，一定要通过特性测试，充分了解锂电池的特性，并研究模型参数的确定方法。不能过分强调模型的形式，而应相应地给出一套适于该模型的参数估计方法。

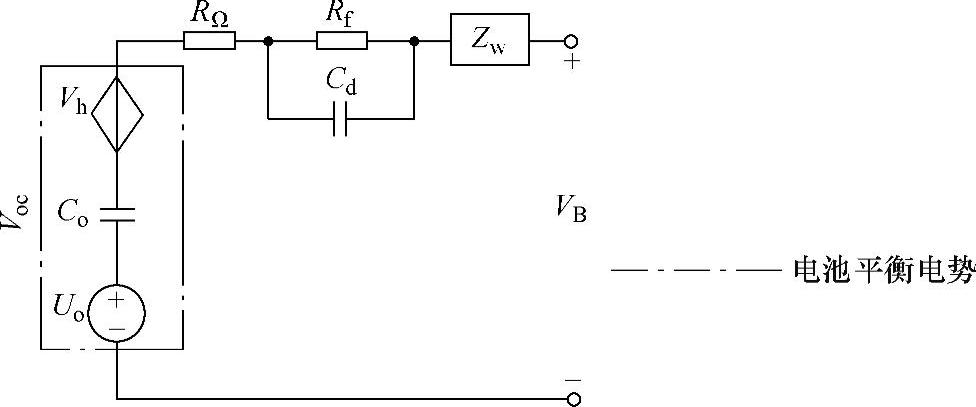
图7-2-14 带有滞回特性的电路模型

R_Ω—电池的欧姆电阻 R_f—电池的极化内阻 C_d—双电层等效电容 Z_w—韦伯阻抗，表示电池中带电粒子的扩散行为，为容性阻抗，类似表示电池的回弹特性的并联RC网络