【摘要】：混凝土在冻融循环作用下，其相对动弹性模量Ed与冻融循环次数n的关系可以用函数表示，即Ed＝f。任何函数都可以用一个多项式表示，同理，本文得到的冻融循环作用下混凝土相对动弹性模量Ed与冻融循环次数n的关系函数的一阶导数可以展开为n的幂级函数，即：对方程两边同时积分得：得：代入边界条件，求得c＝100。
在给出混凝土的损伤演化方程之前，先作如下假设：
①在冻融循环试验之前，混凝土的初始损伤值为0。
②混凝土冻融损伤只是冻融次数的函数，不考虑冻融温度范围、孔隙率等其他因素的影响。
混凝土在冻融循环作用下，其相对动弹性模量Ed与冻融循环次数n的关系可以用函数表示，即Ed＝f（n）。该函数满足以下边界条件：
（1）当冻融循环次数n＝0时，Ed＝100；
（2）函数Ed＝f（n）＞0。
任何函数都可以用一个多项式表示，同理，本文得到的冻融循环作用下混凝土相对动弹性模量Ed与冻融循环次数n的关系函数的一阶导数可以展开为n的幂级函数，即：
对方程两边同时积分得：
得：
代入边界条件（1），求得c＝100。
即：
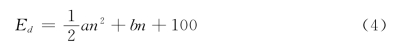(www.xing528.com)
混凝土损伤D：
即：
式中，n为冻融循环次数；
A′，b′为与混凝土材料有关的系数。
按上述相对动弹性模量演化方程，对冻融循环作用下试验结果进行拟合，如图8－1所示，拟合公式为：
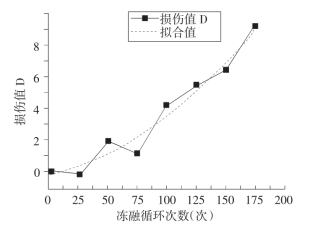
图8－1 冻融循环损伤拟合图
进一步考虑水胶比、粉煤灰掺量、硅灰掺量以及含气量对混凝土损伤的影响，建立混凝土冻融损伤演化方程一般形式：
式中，kfa、ksf、ka分别为粉煤灰掺量、硅灰掺量、含气量和盐冻耦合等单因素下试件的冻融损伤修正系数。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
