为了简化计算,首先将树状结构所有分枝的计算长度系数μ假设为1.0,即先不考虑计算长度系数的影响。随着节点级数的增加,饱和态树状结构的单元个数会急剧增加,所需要的迭代次数也会相应增加。由于分枝构件长度太大时,该构件不可能成为高效能构件,因此,将五级分枝中长度大于0.5m的分枝构件首先去除,优化之前的树状结构如图9—7所示。本算例中将前500次迭代计算设定为拓扑优化+找形分析,500次迭代计算以后进入图9-5所示的模块Ⅱ,即500次以后的优化内容包括找形、拓扑和构件长度优化,3种优化同时进行。本算例中将各级分枝中的优化目标M1、M2、M3、M4、M5分别为2、4、8、16、32。
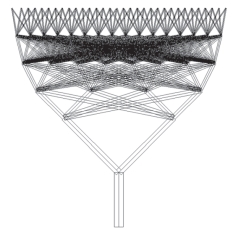
图9-7 迭代初始形状
图9—8列出了当迭代次数为6次、50次、120次、186次、500次、1800次、3000次和6000次时的树状结构形貌特征。由于前500次为树状结构的找形和拓扑优化,因此,该部分迭代计算的目的是去除低效能构件。在该过程中各个节点的竖向坐标不发生改变。从图中所示结果可以看出,各级分枝数量符合预先设定的优化目标。在树状结构找形的同时,所提出的算法可以精确地选出高效能分枝,去除低效能分枝。由迭代结果可知,在预先设定的优化目标时,树状结构的最优拓扑趋向于二分枝树状结构。
当迭代次数超过500次以后,分枝长度优化算法开始介入,该算法将根据每个构件内力大小对其几何长度进行优化。目标是根据木桶原理将整体结构的稳定承载能力提高到最大值。通过观察500次以后迭代过程中树状结构的形貌变化特征可知,树干的截面的实际内力与其稳定承载力的比值低于所有分枝的平均水平,因此长度优化算法增加了树干的长度而减小了上部分枝中实际内力与其稳定承载力的比值高于平均水平的分枝,如5级分枝。通过“取长补短”进而提高整体稳定承载力。由于树状结构左侧荷载大于右侧荷载,因此优化后左侧构件密度大于右侧构件密度,说明该算法可以根据荷载分布自动分配构件的位置。由于右侧分枝的应力水平比较低,导致构件实际内力与稳定承载力的比值偏低,进而引起一级分枝中右侧分枝的长度小于左侧分枝。从图中所示结果可知,经过7000次迭代以后树状结构的形状不再发生变化,即可认为得到了高效的树状结构。
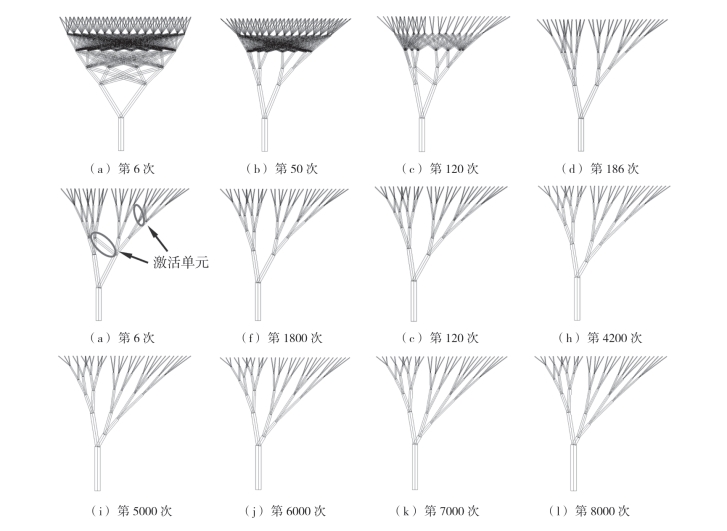
图9-8 优化过程中树状结构形态变化
图9—9所示为优化完成后树状结构在给定荷载作用下的弯矩和轴向力云图。从图中可知,树状结构各个构件的弯矩最大值为0.017N·m,轴向力峰值为7600kN。与轴向力比起来,弯矩很小可以忽略。从该算例可以看出,拓扑优化算法可以在树状结构的找形和长度优化过程中移除低效能构件,激活高效能构件。图9—10所示为9号节点x向和z向位移的收敛曲线。前500次迭代主要是找形和移除低效能构件,从图9—10(a)所示曲线可以看出,迭代500次时,9号节点的x向位移已不再发生变化。迭代500次以后,长度优化算法介入,此时x向位移有突变,随后在0左右浮动变化,这是由于构件长度变化引起的,但是浮动值在±2.5mm以内可以忽略。
图9—10(b)所示为9号节点z向位移的收敛曲线。前500次z向位移不参与迭代,所以并无实际意义。500次迭代以后的z向位移逐步减小至0,说明构件长度趋于稳定。(https://www.xing528.com)
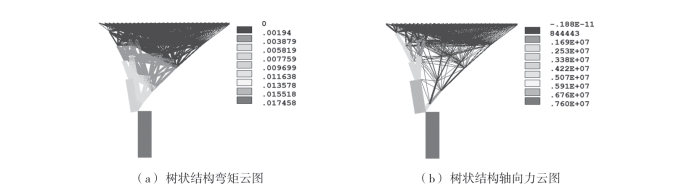
图9-9 优化后树状结构内力云图
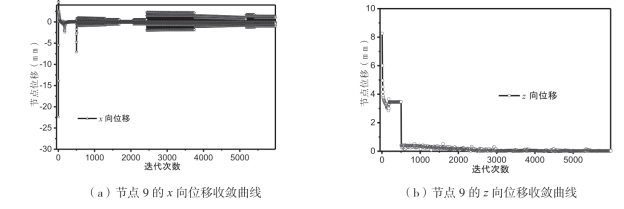
图9-10 节点9坐标收敛曲线
为了对比树状结构在不同荷载作用下树状结构的拓扑和形状,将图9-6所示的非均布荷载转变为均布荷载,即每个节点所承受荷载为80kN,得到的最终树状结构如图9-11所示。从结果可以看出,均布荷载下的树状结构与非均布荷载不同,在规定的优化目标下,均布荷载下的树状结构趋近于二分枝树状结构。

图9-11 均布荷载下的树状结构
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




