将所提出的优化方法(IFFM)用于球面网壳结构的找形分析。所分析的球面网状壳结构的几何尺寸如图8—13所示。在此分析中,最初假定和的值相同。在优化过程中,确定了球面网壳结构的跨度和高度两个几何参数。在优化过程中,其他节点的位置可以自由移动。
根据情形Ⅰ、情形Ⅱ、情形Ⅲ,进行了3种找形分析,不同情况下的荷载和初始形状见图8—14(a),F1表示除中心节点外的节点所受力,F2表示中心受力节点。图8—15和图8—16中示出了优化前后内力云图。轴向力和弯矩显著降低50%,内力分布得到改善。收敛曲线如图8—17所示。用ANSYS进行了200次迭代分析,结果趋于一致。因此,该方法对球面网壳结构是有效的。
节点累积位移受荷载组合的影响。不同条件下得到的优化形状如图8—14(b)和(c)所示。杆件长度是自动优化的,可以根据内力的相对大小进行调整。由于F2的增加,情形Ⅱ中网壳结构顶部杆件长度明显小于情形Ⅲ。
进行特征值屈曲分析,比较优化前后的屈曲承载力,如图8—18所示。优化后的网壳结构在高阶和低阶(1~5阶和30~100阶)下的荷载系数均大于优化前的荷载系数。用第一特征值表示的荷载系数在实际情况下是有意义的。因此,比较了第一阶荷载系数。对于优化后的结构,情形Ⅰ和情形Ⅱ得出的荷载系数分别为37.41和4.18。结构优化前的荷载系数分别为25.41和2.54。这些结果表明,屈曲能力提高了47.2%和64.6%。情形Ⅲ中得出的一阶荷载系数对于优化结构为1.60,对于未优化结构为-6.23。负号表示情形Ⅲ所示荷载在优化前不能由结构支撑,但在优化后可以得到支撑。因此,可以消除杆件的弯矩,并大大提高整个结构的屈曲能力。杆件的屈曲也可以通过根据杆件的轴向力来调整杆件的长度来考虑。

图8-13 球面网壳结构的几何尺寸
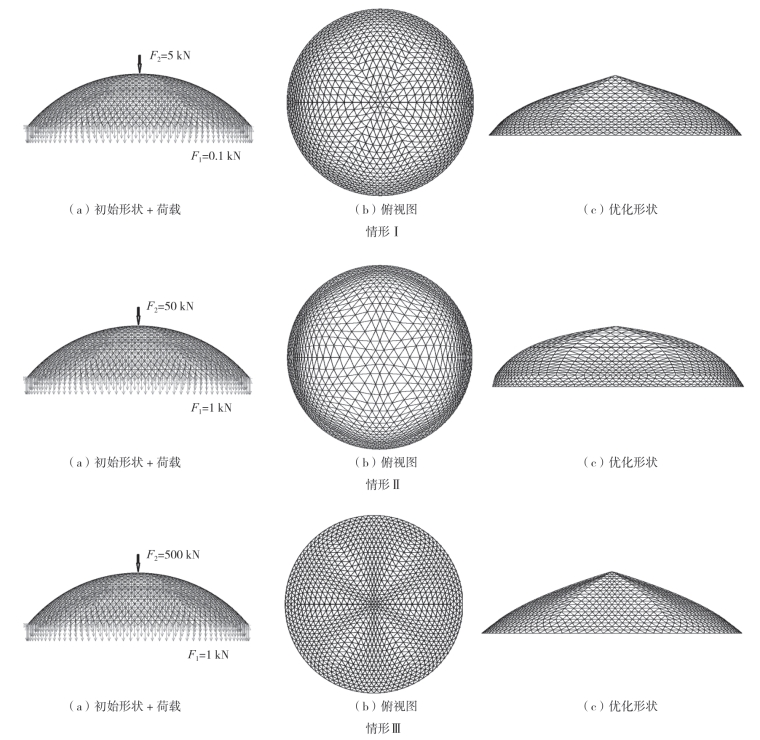
图8-14 球面网壳结构优化形状(A=0.0001, I=0.000002)
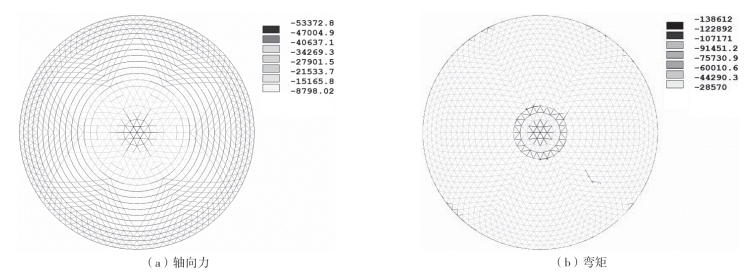
图8-15 优化前球面网壳结构的内力云图(https://www.xing528.com)

图8-16 优化后球面网壳结构的内力云图
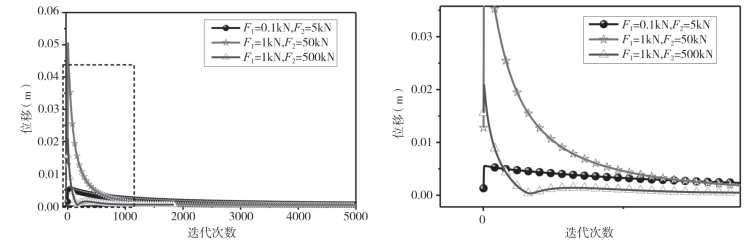
图8-17 球面网壳结构的收敛曲线
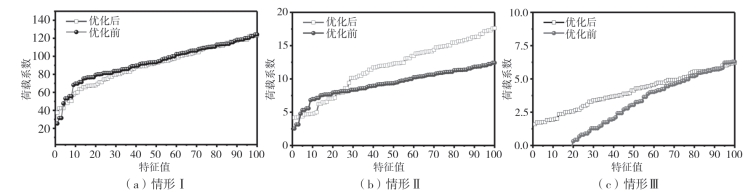
图8-18 屈曲承载力比较
优化设计通常会导致较大程度的缺陷敏感性。本研究以非线性弹性屈曲分析来探讨优化结构的缺陷敏感性。采用情形Ⅲ的初始形状和荷载条件。将F1和F2的值设置为10kN和5000kN,以分析缺陷敏感性。在基本模态缺陷法中,假设缺陷分布与第一屈曲模态一致。最大节点缺陷Δmax设置为α×L/300,其中L和α表示圆顶的跨度和缺陷系数。面积(A)和面积二阶矩(I)设置为1×10-4m2和2×10-4m4。如图8—19所示,荷载因子随缺陷因子的变化趋势表明,优化后的结构对几何缺陷更为敏感。当缺陷达到0.5时,荷载系数趋于稳定。虽然球面网壳对几何缺陷敏感,但优化后的网壳结构的荷载系数远大于优化后的网壳结构。
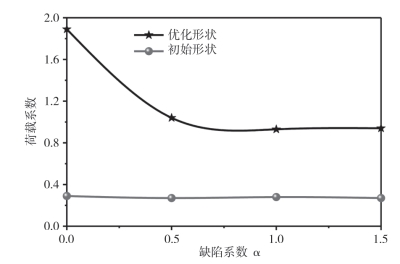
图8-19 荷载系数随缺陷系数的变化趋势(A=0.0001, I=0.0002)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




