该方法可以得到不同荷载组合或约束条件下网壳结构的优化形状。在上述分析中，节点的垂直坐标没有改变，从而导致图8—4（a）所示的问题，即结构上部杆件的长度小于下部杆件的长度。相反，下部杆件的轴向力远大于上部杆件的轴向力。根据欧拉临界载荷，这是不合理的。下部杆件可能发生屈曲，而上部杆件的应力仍然非常低。连续体结构与网壳结构的主要区别在于，在处理网壳结构时，应认真考虑杆件的失稳问题。杆件的整体优化布局应优先考虑材料的强度。所有杆件同时屈曲是合理的，这样不会浪费材料。一根杆件的屈曲承载力可按公式（8—1）表示。
公式（8—1）中μ为有效长度系数，与连接件的抗弯刚度有关；l表示构件的长度；E和I分别表示弹性模量和面积二阶矩。
不同构件之间的连接可视为半刚性连接，其侧向位移受相邻构件的约束。因此，网壳结构中的构件可视为具有弹性侧向支撑的半刚性梁，如图8—8所示。
柱在临界屈曲条件下的平衡微分方程为公式（8—2）。
公式（8—2）和（8—3）中，x代表沿跨度的坐标，y代表横向节点位移，l表示梁的长度，μ是考虑半刚性约束的梁的有效长度系数。
图8-8 弹性横向支承半刚性梁模型
公式（8—2）的一般解可以给出如下：
系数A～D可通过考虑桩的边界条件得出，其可概括如下：(www.xing528.com)
其中S1和S2是约束的转动刚度，S3是横向刚度。
公式（8—9）可由公式（8—4），代入公式（8—5）、公式（8—6）、公式（8—7）、公式（8—8）得出。然后，通过求解公式（8-9）可得出有效长度系数。
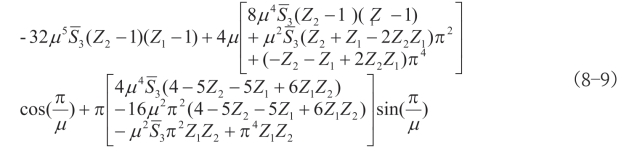
其中，
，Z1和Z2是旋转刚度系数，
。
网壳结构中各杆件的临界应力应相同，以避免材料浪费。对应于屈曲的临界应力可以通过公式导出。
式中，A是杆件的横截面积。构件的长度可推导如下：
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
