【摘要】:首先研究了不同加载条件下的优化形状,同时验证了该方法的适用性。因此,构件长度不受内力绝对值的影响。网状结构的几何尺寸相同,初始形状和荷载条件如图7—7所示,分析了4种不同的加载条件,从不同情况导出的优化形状。该方法可用于各种荷载条件,包括不同方向的力。提取了第四种方案的内力云图,结果如图7—8所示,弯矩远小于轴向力,表明找形分析成功。低轴向力构件的长度大于高轴向力构件的长度。
利用所提出的强耦合优化算法对一个网壳结构进行了找形和优化分析,优化后的网壳结构形状必须与荷载类型和荷载位置密切相关。首先研究了不同加载条件下的优化形状,同时验证了该方法的适用性。图7—6给出了网状结构的几何尺寸和初始形状,为了简单起见,假定有效长度系数、截面积和惯性矩相同(表7—1),施加了两个垂直荷载。构件长度根据内力自动调整。然而,该方法只能生成相对几何长度,而不是绝对几何长度,因为建筑高度已经确定。因此,构件长度不受内力绝对值的影响。

图7-6 不同荷载条件下的优化形状
表7-1 所有构件的几何参数

在找形分析过程中调整了垂直坐标。随后,对构件长度进行了调整。找形分析与优化分析紧密结合,同时考虑了水平荷载对网壳结构形状优化的影响。网状结构的几何尺寸相同(图7—6),初始形状和荷载条件如图7—7所示,分析了4种不同的加载条件,从不同情况导出的优化形状。该方法可用于各种荷载条件,包括不同方向的力。提取了第四种方案的内力云图,结果如图7—8所示,弯矩远小于轴向力,表明找形分析成功。低轴向力构件的长度大于高轴向力构件的长度。(https://www.xing528.com)
结果表明,经过4000次迭代后,节点水平位移接近于零,经过18 000次迭代后,节点垂直位移接近于零。Rave趋于稳定,因为公式(7—2)中所有影响因素的R值趋于相同。

图7-7 不同水平力作用下形状优化
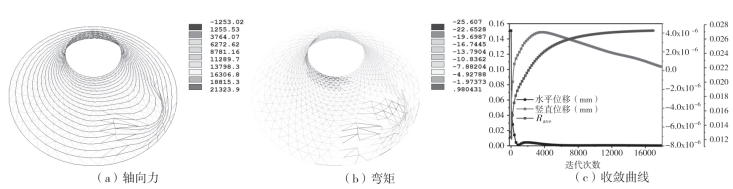
图7-8 内力云图(方案Ⅳ)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




