经找形分析，构件主要受轴向力。各构件的屈曲承载力可从公式（7—2）中求得。各构件的屈曲承载力与材料的截面特性、几何长度和弹性模量密切相关。有效长度系数可以使用前一节中介绍的方法确定。
当各构件同时屈曲时，可以使整体结构的屈曲承载力达到最大。这种情况是由于屈曲能力总是由屈曲能力最低的构件根据木桶原理确定的。特别是要加强薄弱环节，弱化薄弱环节。
构件轴向力与屈曲承载力之比R可用公式表示。然后，当每个分量的R值相同时，这些分量可以同时屈曲。此外，屈曲承载力可以最大化。EI的值被认为是常数，因为它是在设计阶段确定的。有效长度系数与转动刚度密切相关，在特定连接处视为常数。因此，可以通过改变每个组件的几何长度来优化R。
其中F是在给定荷载作用下的实际轴向力。
当R较大时，构件处于风险中。这种风险可以通过减小几何长度来降低。同样，当R的值很小时，几何长度也可以增加。在数值模型中施加温度荷载可以改变几何长度。这种方法也被称为虚拟温度法。各构件的温度荷载按R的相对值确定，R的平均值按公式（7—3）计算。
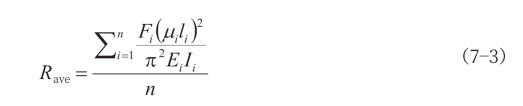
式中，Fi、μi、li和EiIi分别是第i个分量的轴向力、有效长度系数、几何长度和截面特性；n是优化中包含的分量数。Ri与Rave之差可按公式（7—4）计算，而第i分量之温度负荷可按公式（7—5）计算。
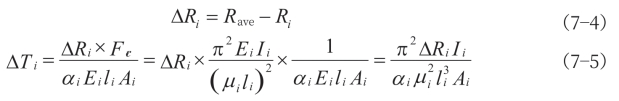(www.xing528.com)
式中αi和Ai分别是第i分量的线膨胀系数和截面积。
当Rave大于Ri时，应向第i个部件施加正温度载荷。因此，第i个组件的几何长度应该增加。值得注意的是，当受拉构件不存在屈曲现象时，可以对所有构件或仅对受压构件执行优化。图7—1为不同条件下构件长度优化的示意图。在优化过程中，张拉构件的长度可以保持不变。在某些情况下，也可以优化张拉构件的长度，以保持均匀的网格尺寸。
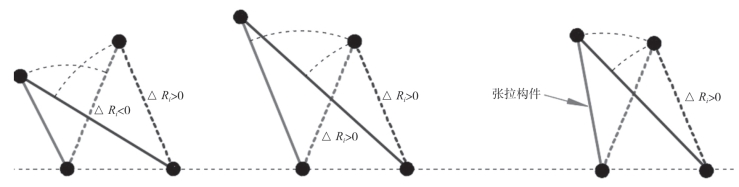
图7-1 基于轴向力的长度优化示意图
该方法的主要目的是通过形状优化来减小构件的弯矩，通过改变节点位置来优化构件的长细比。优化方程可表示为：
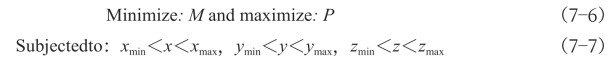
M为构件弯矩；P为整体结构的屈曲承载力；xmin、ymin、zmin为设计中的最小节点坐标；xmax、ymax、zmax为设计中的最大节点坐标。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
