通过前一节中介绍的建立拓扑结构的方法可以用来进行找形分析。对图4—7(b)和图4—8(c)所示的树状结构进行找形分析。在如图4—12所示的树状结构顶部的每个节点施加10kN的垂直载荷。找形优化后结构的几何形态如图4—13所示。由此可见,所提出的建立拓扑结构的找形方法可用于具有平面和球面的树状结构。树状结构的形态在找形分析过程中也是不断变化的。在先前的验证中,建立拓扑结构的优化方法在具有平面表面的树状结构中已经得到了验证。

图4-12 找形优化前树状结构的几何形状
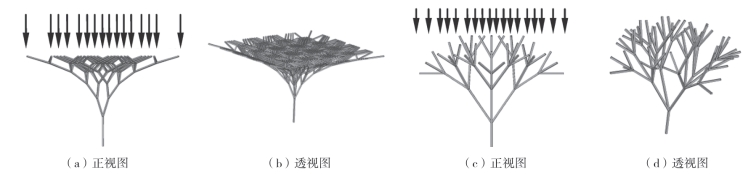
图4-13 找形优化后树状结构的几何形状
在给定载荷作用下,具有球形表面的树状结构的内力分布如图4—14所示。这表明树状结构在荷载的作用下轴向力远大于弯矩。因此,弯矩可以忽略不计。图4—14(b)所示的结果表明,存在于最高层的构件的弯矩明显大于其下一层的构件的弯矩,并且树状结构的分枝在水平方向上的弯矩也明显大于下一层的构件在倾斜方向上分枝的弯矩。具有球形表面的树状结构的所有部件,除了单独的水平分枝外,仅承受轴向力。本节研究了节点坐标的偏移历史,在对称位置中提取4个节点的坐标,并在图4—15中示出。该图表明所提出的方法在优化树状结构的最佳配置方面具有很突出的高效性。
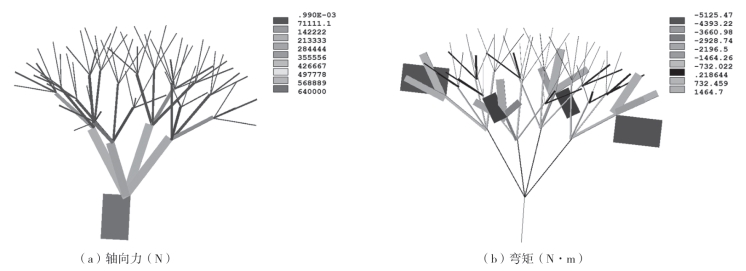
图4-14 树状结构的内力(https://www.xing528.com)
如果只采用单一连接类型,最高级的分枝数目将非常大。因此,为解决在实际工程项目中可能需要多个连接类型。如图4—16所示,通过提出的建立拓扑结构的方法建立和优化了具有5—4—3—2连接类型的分枝结构,最高级的分枝数量就可以大幅减少。图4—16(b)显示了在找形分析之后的树状结构的构造,其中只有节点的水平分量已经移动,垂直方向上的节点坐标不变。在树状结构的所有自由端上都施加了10kN的垂直载荷。在给定载荷作用下,各分枝的内力如图4—17所示。该图表明树状结构的轴向力远大于弯矩。因此,弯矩可以忽略不计。
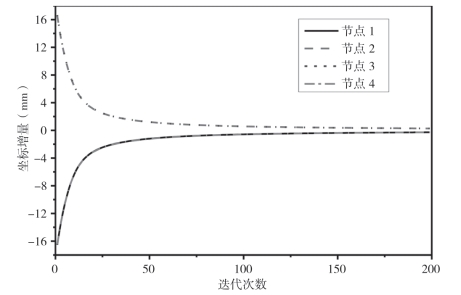
图4-15 节点移动历史记录
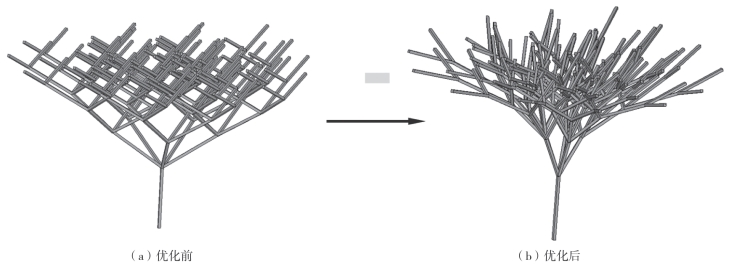
图4-16 具有多种连接类型的分枝结构
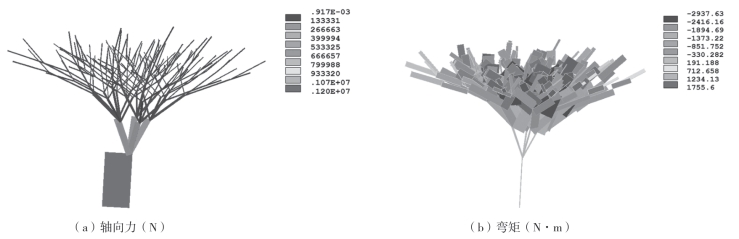
图4-17 优化后的内力
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




