树状结构的构件可根据它们相对于树干的位置进行分类,如图4—1所示,从树干发芽的分枝被定义为一级分枝,并且从一级分枝分出来的构件被定义为第二级分枝。从第i级分枝中生长的分枝被定义为第(i+1)级分枝。拓扑建立前应注意的几组主要几何参数,如图4—2所示。

图4-1 树状结构的部件分类

图4-2 树状结构几何参数
Hi表示垂直方向上的i级分枝的高度,H0表示树干的高度。参数Li表示分枝在其轴向方向上的第i级分枝的长度。参数φ表示一个分枝在轴向与其上一级分枝的夹角。
树状结构的连接也可以根据下层分枝的数量来分类,图4—3中示出了不同连接类型的示意图。当一个层次上的所有连接类型都相同时,一个树状结构的连接可以表示为A、B、C、D……
这里,A、B、C和D分别表示第一、第二、第三和第四级的连接类型。
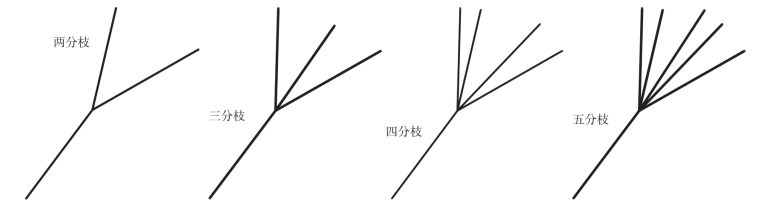
图4-3 连接节点类型
树状结构的拓扑结构可以根据上述几何参数用各种有限元程序生成。本节采用ANSYS参数化设计语言进行拓扑建立,拓扑建立的工作流程如图4—4、图4—5所示。
(1)平面表面拓扑建立流程图
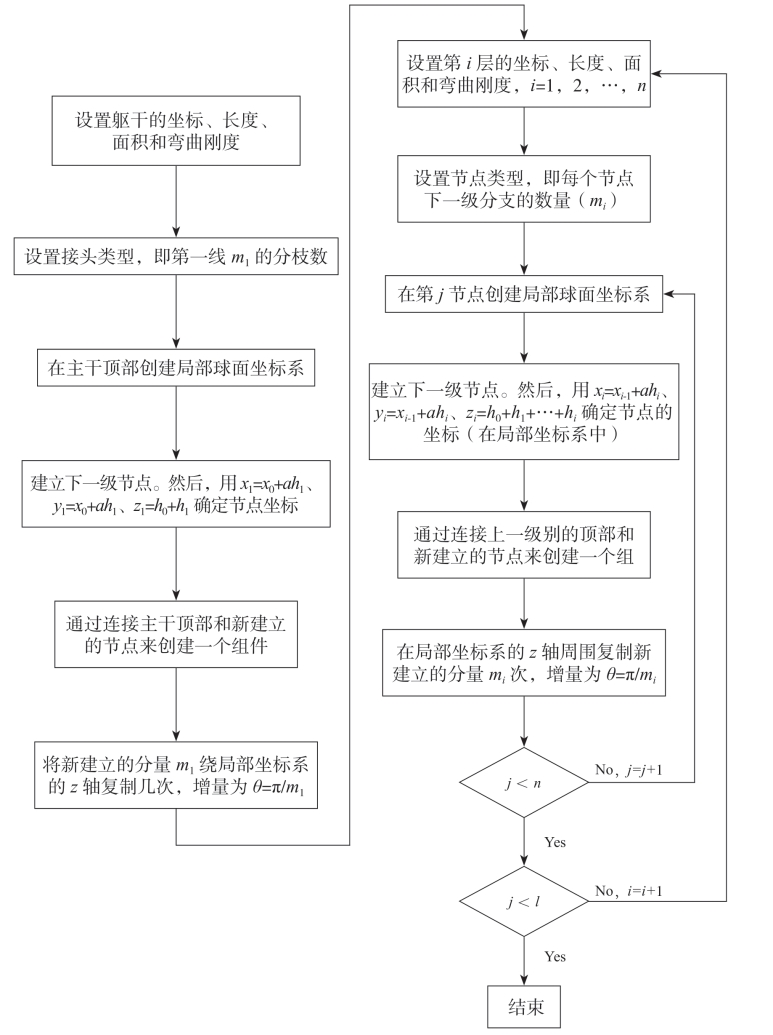
图4-4 平面表面拓扑建立流程图
(2)球面表面拓扑建立流程图(https://www.xing528.com)

图4-5 球面表面拓扑建立流程图
如图4—6所示,如果属于相同水平的部件具有均匀的长度,则可以获得具有球形表面的树状结构。
如图4—7所示,如果属于相同水平的部件具有均匀的高度,则可以获得具有平面表面的树状结构。
在图4—6~图4—8中示出了具有不同级别的树状结构。图4—6和图4—7所示的树状结构是根据图4—5所示的工作流程建立的,如图4—3所示,图4—6所示的树状结构具有均匀的单元长度l=1m,所有连接都设置为4个分枝类型。
图4-7所示的树状结构的上层分枝的长度是下层分枝长度的0.8倍,即li/li-1=0.8。所有连接被设置为4个分枝类型。
例如图4—8所示具有平面表面的分枝结构。

图4-6 等长分枝树状结构的几何形状(球面)

图4-7 不同长度分枝的树状结构的几何形状(球面)

图4-8 树状结构的几何形状
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




