4.3.1 4-12-2分枝树状结构
以本节提出的方法为基础,对空间树状结构进行了分析。首先分析了均布荷载作用下的结构,空间树状结构的初始几何形状如图3—19(a)所示,它是通过环向复制前述的平面树结构而得到的。在上弦杆上施加10kN的点荷载,得到相应的优化几何模型如图3—19(b)所示,结构内部弯矩的分布如图3—19(c)所示,最大弯矩为0.001N·m。
然后分析了非均匀分布荷载作用下的空间树状结构。在位于上弦节点的一部分施加80kN的荷载,如图3—20(a)所示,其他节点施加10kN的荷载。在非均匀分布荷载作用下计算导出的最优形式如图3—20(b)所示。
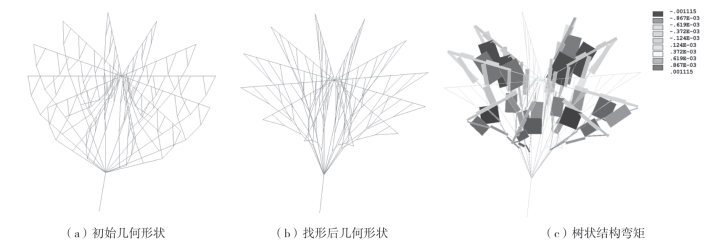
图3-19 树状结构初始几何形状
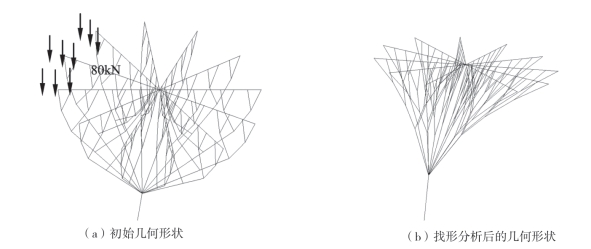
图3-20 树状结构初始几何形状
4.3.2 5-6-4-4-4-2分枝树状结构
通过本节提出的方法,在Hunt、武岳等人提到的三级、四级分枝树状结构的基础上,继续进行五级树状结构的找形分析,设置树状结构为五级6—4—4—4—2分枝,在最外层节点处每个节点施加10kN的集中力。通过通用有限元程序ANSYS的建立模型如图3—21(a)所示,结构内部弯矩的分布如图3—21(c)所示,通过数据可以发现最大弯矩为41.8938N·m。
然后分析了非均匀分布荷载作用下的空间树状结构。在位于上弦节点的一部分施加80kN的荷载,如图所示,其他节点施加10kN的荷载。在非均匀分布荷载作用下计算导出的模型如图3—22(a)所示。通过数据可以发现最大弯矩为-106.968N·m。

图3-21 均布荷载作用下树状结构几何形状
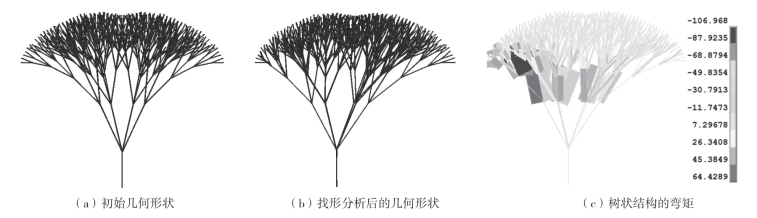
图3-22 非均布荷载作用下树状结构几何形状
4.3.3 5-6-4-4-2-2分枝树状结构
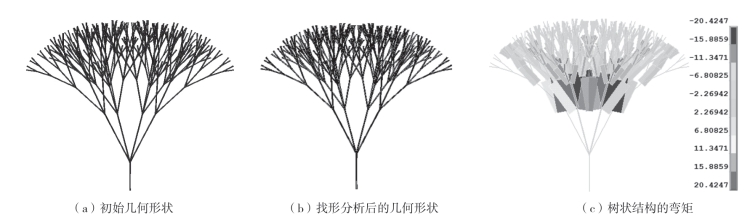
设置树状结构为五级6—4—4—2—2分枝[图3—23(a)],在最外层节点处每个节点施加10kN的集中力。通过通用有限元程序ANSYS的找形分析得到图3—23(b)的找形结果,结构内部弯矩的分布如图3—23(c)所示,通过数据可以发现最大弯矩为20.4247N·m。
然后分析了非均匀分布荷载作用下的空间树状结构。在位于最外层节点的一部分施加80kN的荷载,如图3—24(a)所示,其他节点施加10kN的荷载。在非均匀分布荷载作用下计算导出的最优形式如图3—24(b)所示。通过数据可以发现最大弯矩为-68.5732N·m。
 (https://www.xing528.com)
(https://www.xing528.com)
图3-23 均布荷载作用下树状结构几何形状
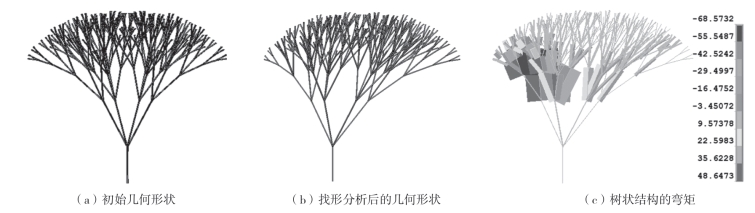
图3-24 非均布荷载作用下树状结构几何形状
4.3.4 5-6-4-2-2-2分枝树状结构
设置树状结构为五级6—4—2—2—2分枝[图3—25(a)],在最外层节点处每个节点施加10kN的集中力。通过通用有限元程序ANSYS的找形分析得到图3—25(b)的找形结果,结构内部弯矩的分布如图3—25(c)所示,通过数据可以发现最大弯矩为14.7532N·m。
同样分析了非均匀分布荷载作用下的空间树状结构。在位于外层节点的一部分施加80kN的荷载,如图3—26(b)所示,其他节点施加10kN的荷载。在非均匀分布荷载作用下计算导出的最优形式如图3—26(c)所示。通过数据可以发现最大弯矩为63.7538N·m。
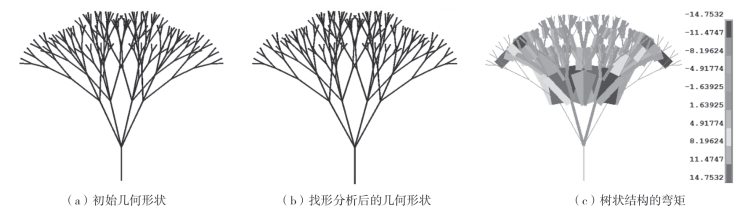
图3-25 均布荷载作用下树状结构几何形状
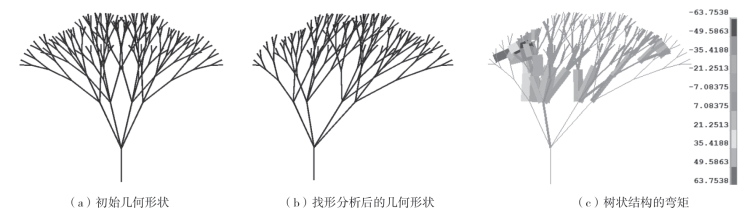
图3-26 非均布荷载作用下树状结构几何形状
4.3.5 5-6-2-2-2-2分枝树状结构
设置树状结构为五级6—2—2—2—2分枝[图3—27(a)],在最外层节点处每个节点施加10kN的集中力。通过通用有限元程序ANSYS的找形分析得到图3—27(b)的找形结果,结构内部弯矩的分布如图3—27(c)所示,通过数据可以发现最大弯矩为20.1438N·m。
然后分析了非均匀分布荷载作用下的空间树状结构。在位于上弦节点的一部分施加80kN的荷载,如图3—28(a)所示,其他节点施加10kN的荷载。在非均匀分布荷载作用下计算导出的最优形式如图3—28(b)所示。
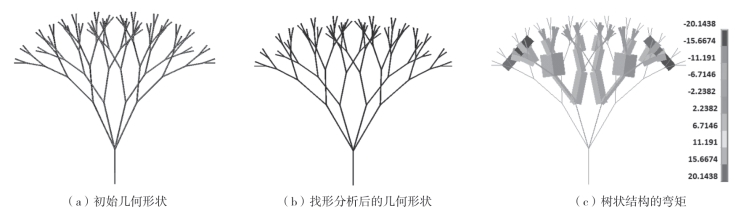
图3-27 均布荷载作用下树状结构几何形状
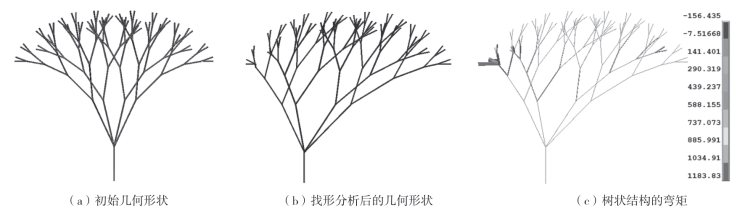
图3-28 非均布荷载作用下树状结构几何形状
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




