【摘要】：为了达到简化的目的，通常采用图3—3所示的分析模型进行验证。如图3—8所示，将通过计算找形后所得树状结构的最优形状与Hunt所得到的最优形状进行对比研究。从计算结果可以看出，计算所得结果与Hunt所得结果高度吻合，说明本节基于双单元的找形迭代程序具有很高的精度，同时具有很高的效率，验证了该方法的准确性和可靠性。
采用双单元法对平面和空间树状结构进行找形分析。可以通过人为的方式增加杆单元的刚度来最大限度地减小构件在树状结构中的轴向变形。这样，构件在轴向力作用下的变形就可以忽略不计了。反之，截面惯性矩减小，则构件在弯矩作用下的变形可以达到最大化。为了达到简化的目的，通常采用图3—3所示的分析模型进行验证。本节中还采用这种简化的方法对提出的找形方法的精度和有效性进行了验证。
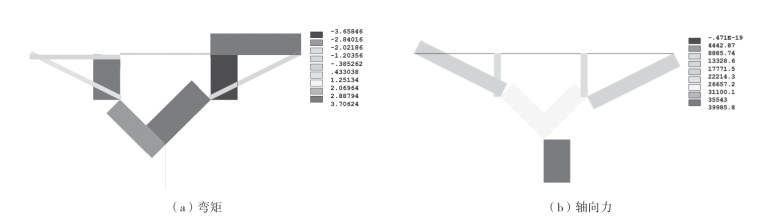
本节研究了抗弯刚度对收敛性的影响，将杆单元的截面面积设为0.001m2，则树状结构不同惯性矩的内力分布如图3—4～图3—6所示。
如图3—7所示，得出构件的弯矩和找形分析前后得出的节点位移。结果表明，找形后得到的弯矩远小于找形分析前得到的弯矩。同样，找形分析后得到的节点位移接近于零。这就表明，在给定的荷载作用下，树状结构中的构件主要受轴向力作用，并在荷载作用下处于平衡状态。
如图3—8所示，将通过计算找形后所得树状结构的最优形状与Hunt所得到的最优形状进行对比研究。从计算结果可以看出，计算所得结果与Hunt所得结果高度吻合，说明本节基于双单元的找形迭代程序具有很高的精度，同时具有很高的效率，验证了该方法的准确性和可靠性。
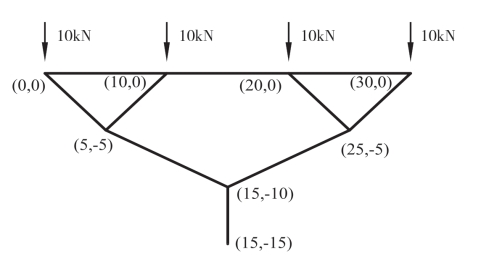
图3-3 分析模型
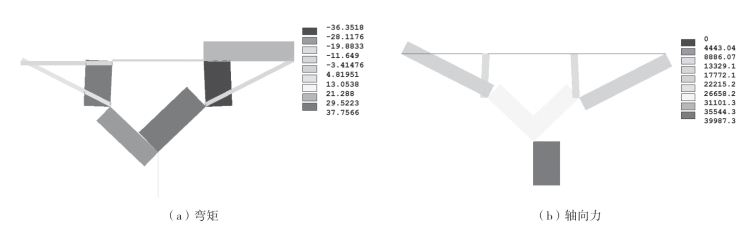
图3-4 树状结构初始云图（I = 2×10-8m4）
(www.xing528.com)
图3-5 树状结构初始云图（I= 2×10-9m4）
图3-6 树状结构初始云图（I = 2×10-10m4）
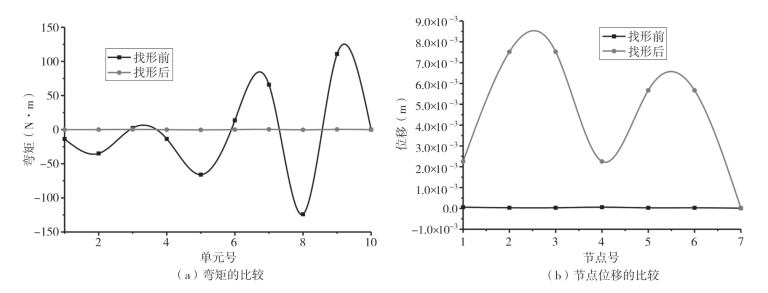
图3-7 找形分析前后的结果比较
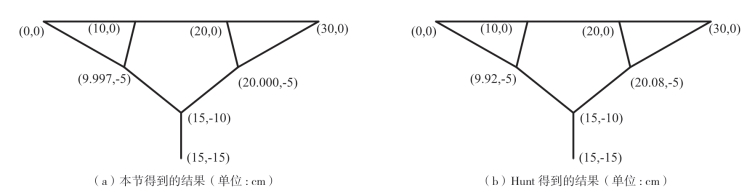
图3-8 提出的方法的验证
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
