凯威特单层网壳稳定性研究的成果

6.1.1　网壳结构的选型

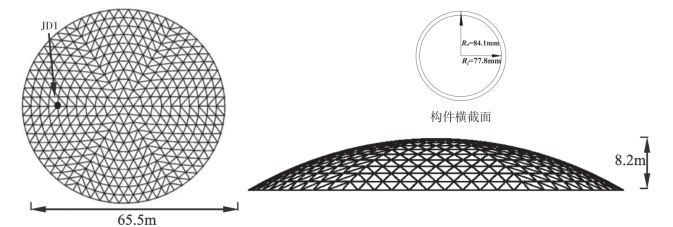
图2-75　凯威特网壳

球面网壳有多种网格划分形式，本文以凯威特K6型大跨度单层网壳结构为例进行研究，网壳的杨氏模量为2.1×105MPa，屈曲载荷为345MPa。网壳如图2—75所示，在本文的有限元分析中网壳每个节点施加2000kN的力，每根杆件被分割为20份。

6.1.2　杆件初弯曲对网壳稳定承载能力的影响

假定网壳无节点安装误差，只考虑在节点刚度的影响下，单层网壳杆件初弯曲vm0取值分别为l/1000、10l/1000、50l/1000、100l/1000时网壳的概率屈曲分布，如图2—76所示。显然从图中可以看出，无论节点刚度和杆件初弯曲幅值如何变化，单层网壳的屈曲系数都满足对数正态概率分布。图2—76（a）给出了节点刚度为0.1时单层网壳屈曲系数分布曲线，当杆件初始弯曲取值为l/1000、10l/1000、50l/1000、100l/1000时，屈曲系数的对数均值分别为-2.33、-2.26、-2.62、-3.03，与杆件初弯曲为l/1000时的屈曲系数对数均值做比较，可得下降度分别为1.35%、17.49%、35.87%；当节点刚度系数为0.3时，下降度分别为2.60%、33.33%、56.25%；节点刚度为0.5时，下降度为3.26%、32.61%、55.98%；节点刚度为1.0时，下降度为2.23%、29.61%、52.51%.可以看出无论节点刚度取何值，随杆件初弯曲缺陷的增大，网壳稳定承载能力显著降低，尤其是当杆件初弯曲幅值增大到100l/1000时，屈曲系数对数均值下降到初弯曲值为l/1000时的一半，因此在实际工程中应将杆件初弯曲控制在l/1000之内。当杆件初弯曲为l/1000，刚度系数为0.1、0.3、0.5、1.0时，屈曲系数对数均值分别为-2.23、-1.92、-1.84、-1.79，与刚度为0.1时的屈曲系数对数均值做比较，上升度分别为13.90%、17.49%、19.73%；杆件初弯曲为10l/1000时，上升度为12.83%、15.93%、19.03%；杆件初弯曲为50l/1000时，上升度为2.29%、6.87%、11.45%；杆件初弯曲为100l/1000时，上升度为0.99%、5.28%、9.90%.由此可知当杆件初弯曲为定值时，节点刚度越大网壳稳定承载能力越强，但是当杆件初弯曲大于50l/1000后节点刚度对网壳稳定性能的提高作用就越来越不明显了。因此，在实际工程中为有效提高单层网壳的稳定承载能力，在条件允许的情况下应以控制杆件初弯曲幅值为主。

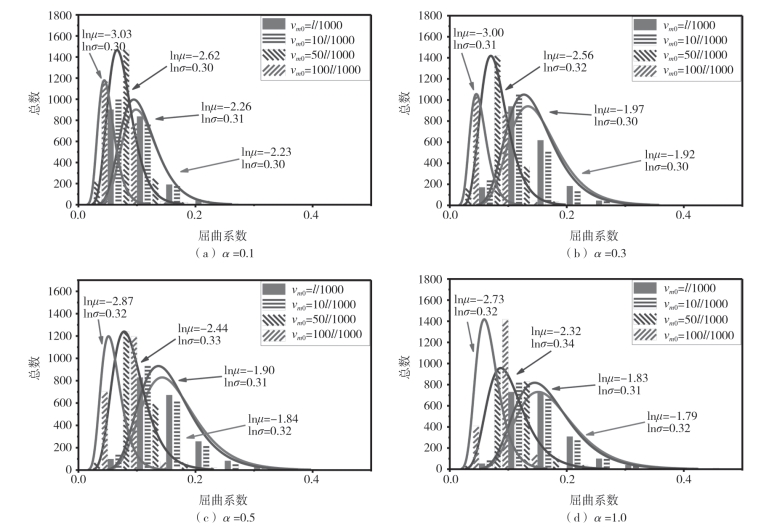
图2-76　杆件初弯曲vm0对屈曲稳定性的影响

为更好地研究屈曲系数与节点刚度之间的关系，绘制了屈曲系数对数均值和对数标准差与节点刚度之间的关系曲线，如图2—77所示。由图2—77（a）可以清晰地看到，网壳的屈曲系数随节点刚度的增大而增大，且随着杆件初弯曲的增大，对应曲线也由上到下依次分布，当杆件初弯曲为l/1000和10l/1000时，屈曲系数随节点刚度变化的曲线互相平行且几乎重合，也就是说当杆件初弯曲幅值由l/1000变化到10l/1000时，网壳极限承载能力不随杆件初弯曲值的变化而变化。由图2—77（b）可知节点刚度和杆件初弯曲的大小与网壳屈曲系数的对数标准差之间没有相关性，无论节点刚度和杆件初弯曲怎么变化，对数标准差都近似为0.31。

图2-77　刚度系数α对屈曲稳定性的影响

以上对网壳屈曲系数的描述和分析，只是基于图像的规律描述，只阐述了图像的直观表象，在实际工程中使用起来不方便、不准确，为了更加准确方便地研究半刚性对网壳屈曲稳定承载能力的影响，将屈曲系数的对数均值、对数标准差分别做了对应初弯曲下刚性连接网壳的归一化处理，得到对数均值和对数标准差随刚度变化的折减系数曲线，如图2—78所示。考虑到实际工程对钢构件的平直度要求，以下只对杆件初弯曲最大幅值为l/1000和10l/1000时的折减系数曲线公式进行研究。由图2—78（a）可以观察到，当杆件初弯曲为l/1000和10l/1000时，折减系数η随刚度系数α的变化曲线几乎是重合的。为得到准确度高的工程指导公式，分两种情况进行公式拟合，得到结果如下：

当刚度小于0.3时，初弯曲为l/1000的曲线处于初弯曲为10l/1000的上方；当刚度系数为0.3～1.0时情况刚好相反，为提高参考公式的准确性，取其最不利情况则：

公式的参数取值由表2-1所示，在实际工程中可以根据不同的工况选择合适的参考公式。由图2—78（b）可以看出对不同工况下的对数标准差进行归一化处理后，曲线近似为一条取值为1的水平直线且在不同缺陷情况下的曲线都重合，因此，无论在什么工况下对数标准差取值均为0.31。则网壳在初弯曲幅值为l/1000和10l/1000时，随节点刚度的不同取值，网壳屈曲系数就满足对数均值为lnη=η·ε[其中η由公式（2—36）计算得到；ε为网壳刚度系数为1.0时的屈曲荷载系数]，对数标准差为lnσ=0.31的对数正态分布，表示为：

概率密度函数为：

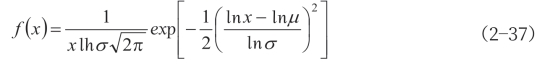
表2-1　折减系数η的曲线拟合公式参数

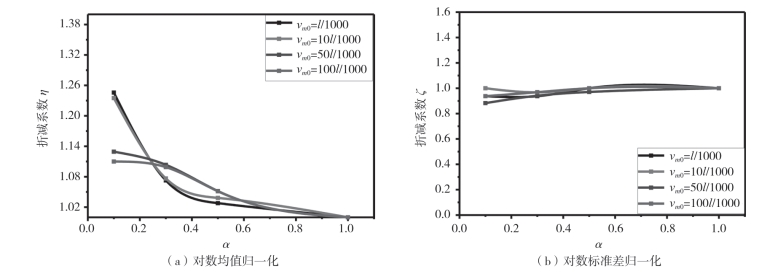
图2-78　对数均值和对数标准差归一化处理(www.xing528.com)

6.1.3　杆件随机初弯曲对网壳稳定承载能力的影响

网壳杆件的初弯曲是由于厂家生产误差、施工工序、测量技术、设备安装等等不确定因素所导致的，具有初弯曲幅值大小和弯曲方向的不确定性，故在结构稳定承载能力评估过程中考虑杆件随机初弯曲才更符合实际工况。本文通过在构件跨中位置指定初始缺陷值vm0，再利用ANSYS提供的均匀分布函数RAND生成在区间[0，1]内均匀分布的随机数，以考虑杆件初弯曲的随机性，对不同工况的网壳分别进行2000次非线性屈曲分析得到如图2—79所示的概率分布曲线。与无随机杆件初弯曲的网壳一样，进行多次迭代计算得到的载荷屈曲系数都满足对数正态分布，图2—79（a）给出了节点刚度为0.1时单层网壳屈曲系数分布曲线，当杆件初始弯曲取值为l/1000、10l/1000、50l/1000、100l/1000时，屈曲系数对数均值分别为-2.33、-2.66、-2.62、-3.01，与杆件初弯曲为l/1000时的屈曲系数对数均值做对比，下降度分别为1.35%、17.49%、35.22%；当节点刚度系数为0.3时，下降度分别为2.09%、19.37%、38.22%；节点刚度为0.5时，下降度为1.62%、17.30%、36.22%；节点刚度为1.0时，下降度为1.12%、16.20%、35.64%。可以看出无论节点刚度取何值，随杆件初弯曲缺陷的增大，网壳稳定承载力显著降低，尤其是当杆件初弯曲幅值超过50l/1000后，承载力屈曲系数明显下降。

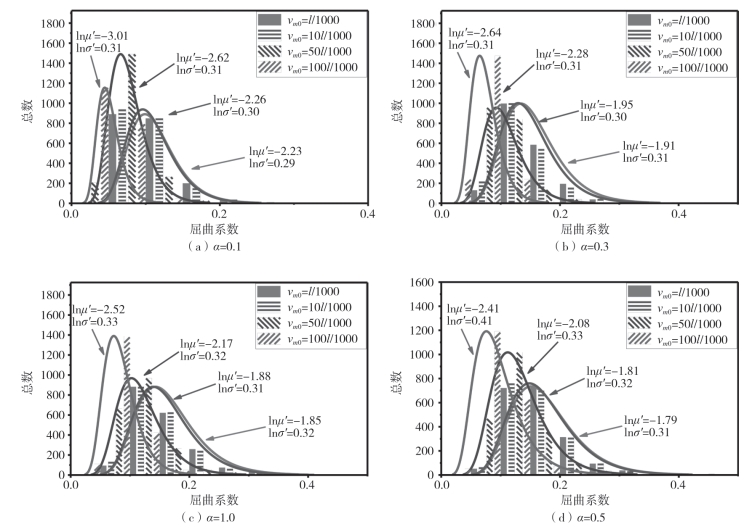
图2-79　杆件随机初弯曲vm0对屈曲稳定性的影响

当杆件初弯曲为l/1000，刚度系数为0.1、0.3、0.5、1.0时，屈曲系数对数均值分别为-2.23、-1.91、-1.85、-1.79，相对于刚度为0.1时的屈曲系数对数均值上升度分别为14.35%、17.04%、19.73%；杆件初弯曲为10l/1000时，上升度为13.72%、16.81%、19.91%；杆件初弯曲为50l/1000时，上升度为12.98%、17.18%、20.61%；杆件初弯曲为100l/1000时，上升度为12.29%、16.28%、19.93%。由此可见随节点刚度的增大网壳屈曲系数上升明显，但由图2—80（a）可以看出，不同工况下的曲线为3条近乎平行的曲线，与不考虑杆件初弯曲的随机性不同，当杆件初弯曲幅值增大到50l/1000后，节点刚度对网壳稳定性的影响还是比较明显的，不会出现断崖式降低。因此，考虑杆件初弯曲的随机性时，能提高节点刚度对网壳稳定性的影响能力。

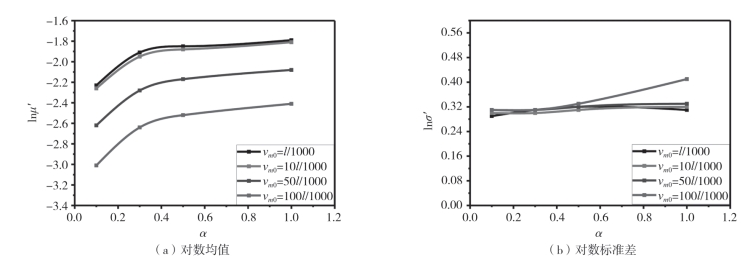
图2-80　刚度系数α对屈曲稳定性的影响

观察图2—81（a），不同初弯曲取值时的折减系数曲线几乎重合，杆件随机初弯曲对折减系数η′ 的影响可以忽略不计，考虑最不利情况，以杆件初弯曲为50l/1000时的曲线为代表。拟合公式如下：

公式的参数取值为：0.1≤α＜1.0，A2=0.417，t2=0.212，η2=0.998。

由图2—81（b）可以看出对数标准差进行归一化后，折减系数μ′ 随刚度变化的曲线几乎重合且为近1的水平直线，则无论杆件随机初始缺陷和节点刚度如何变化，对数标准差都取0.32.则网壳在初弯曲值vm0≤100l/1000时，随节点刚度的不同取值，网壳屈曲系数满足对数均值为（其中η′ 由公式（2—39）计算得到；ε′ 为网壳刚度系数为1.0时的屈曲载荷系数），对数标准差为的对数正态分布，表示为：

概率密度函数为：

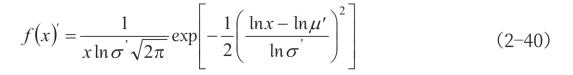
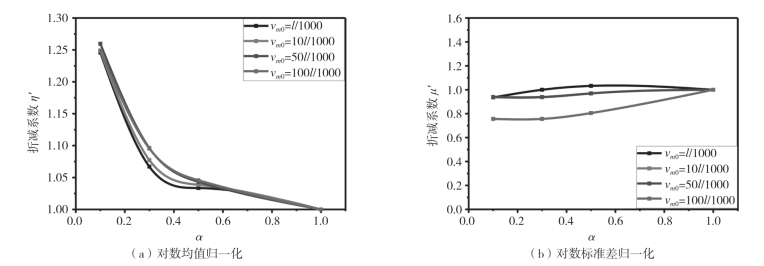
图2-81　均值和标准差归一化处理

6.1.4　杆件初弯曲与杆件随机初弯曲对网壳稳定承载能力影响的对照分析

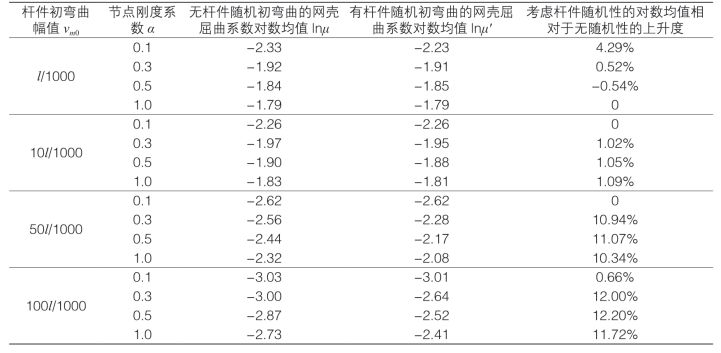
将图2—76和图2—79和中网壳屈曲系数概率分布曲线的对数均值收集归纳如表2—2所示，可以发现当考虑杆件初弯曲幅值的随机性时，无论节点刚度如何变化，网壳的稳定承载能力几乎都提高。当杆件初弯曲值为l/1000节点刚度为0.1、0.3、0.5、1.0时，上升度分别为4.29%、0.52%、-0.54%、0；当杆件初弯曲值为10l/1000时，上升度分别为0、1.02%、1.05%、1.09%。因此，当杆件初弯曲值vm0 ≤10l/1000时，杆件初弯曲的随机性对网壳屈曲系数分布的对数均值几乎没有影响，此时分析单层网壳的安全性可以不考虑杆件初弯曲幅值的随机性，按照无随机性的网壳模型来进行分析足矣。当杆件初弯曲值为50l/1000时，上升度分别为0、10.94%、11.07%、10.34%；当杆件初弯曲值为100l/1000时，上升度分别为0.66%、12.00%、12.20%、11.72%。则当杆件初弯曲幅值50l/1000≤vm0≤100l/1000且刚度系数0.3≤α≤1.0时，lnμ′相对于lnμ的上升度在区间在[10.34%，12.20%]内变化，此时应考虑杆件初弯曲幅值的随机性

表2-2　考虑杆件初弯曲与杆件随机初弯曲对网壳屈曲稳定性的影响对照表