在空间网格结构的稳定性分析中,大多采用一致模态缺陷法来确定缺陷分布规律。然而,这种缺陷的分布方式并不符合实际情况。
在本研究中假定节点安装误差满足均匀分布。节点安装误差(Emax)的大小被设置为不同的值。图2—69显示了节点安装误差的数值模型,图2—70显示了节点安装误差对施威德勒网壳稳定荷载系数的影响。
图2—70显示了节点安装误差在节点刚度设置为不同值时,节点安装误差对施威德勒网壳屈曲荷载系数的影响。一般情况下,施威德勒网壳的稳定承载能力随着节点刚度的增加而增大。结果表明,当节点刚度系数为0.1,Emax=15mm时,理想结构的稳定荷载系数为0.49。缺陷结构的稳定荷载系数从0.24变化到0.3。当Emax设置为45、133和400m时,缺陷结构的屈曲荷载系数分别为0.19~0.26、0.13~0.25和0.1~0.25。此外,节点安装误差对施威德勒网壳屈曲承载能力的影响大于初始曲率的影响。稳定荷载系数的变化范围随节点安装误差Emax的增大而增大。有节点安装误差的施威德勒网壳的稳定承载能力明显低于理想结构。
图2-69 节点安装误差幅值Emax=400mm时的有限元模型
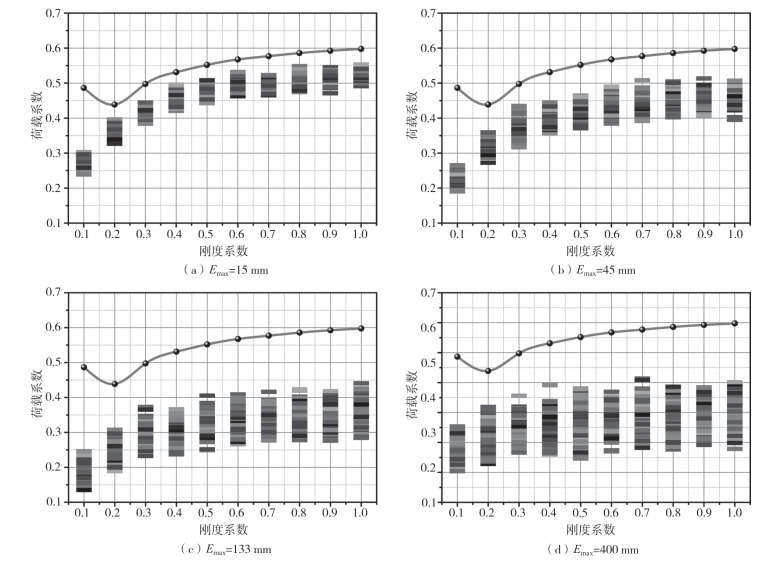
图2-70 安装误差对施威德勒网壳影响
图2—71显示了节点安装误差对K8浅网壳不同节点刚度系数时的稳定荷载系数的影响。图2—71(a)中的结果表明,具有节点安装误差的K8浅网壳的稳定能力可能大于理想结构的稳定承载能力,这与施威德勒网壳不同。节点安装误差对K8网壳的影响小于施威德勒网壳。
图2—72描述了节点安装误差对K8深网壳的影响。结果表明,K8深网壳的荷载系数变化范围较小,即对节点安装误差的敏感性较弱。将缺陷结构的承载能力与理想结构的承载能力进行了比较,研究了折减系数随刚度系数的变化规律。结果表明,某一节点刚度的最小折减系数随Emax的增大而减小。与初弯曲的影响不同,节点安装误差引起的折减系数变化幅度与结构尺寸呈正相关。图2—73显示了当Emax=20mm,α=0.5和1.0时K8网壳的载荷—挠度曲线。如图2—74所示,当节点刚度设置为0.5和1.0时,结构屈曲承载力范围分别为0.61~0.79和0.65~0.87。此外,节点安装误差也会对整体结构屈曲后力学性能产生影响。(https://www.xing528.com)
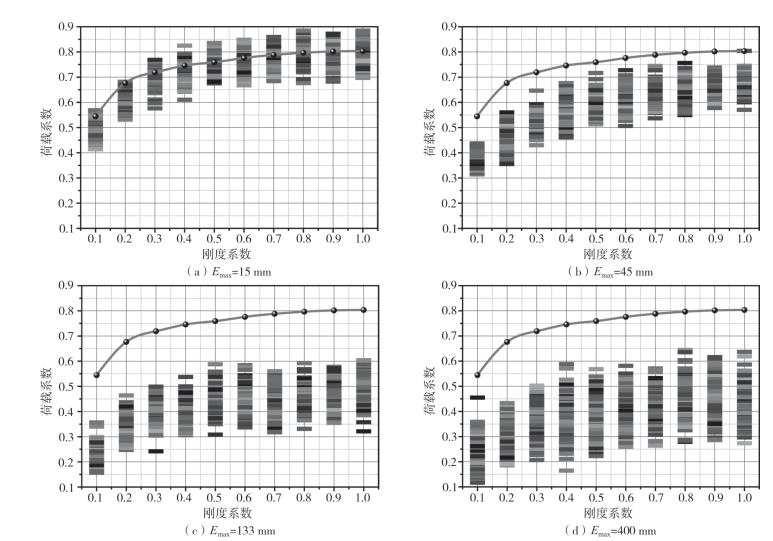
图2-71 节点安装误差对K8浅网壳荷载系数的影响
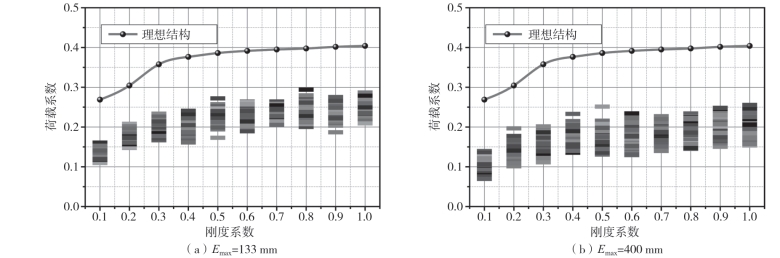
图2-72 节点安装误差对K8深网壳荷载系数的影响
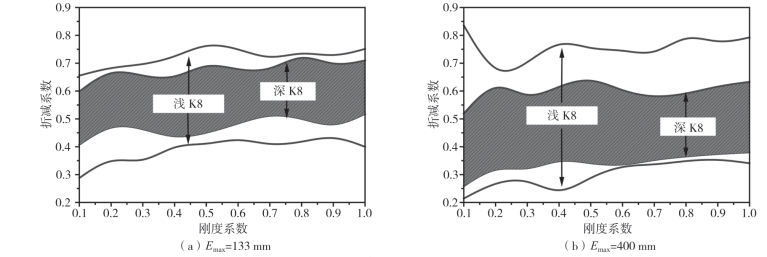
图2-73 折减系数随刚度系数的变化趋势(节点安装误差)

图2-74 K8浅网壳荷载位移曲线
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




