2.3.1 包含缺陷单元的刚度矩阵
图2—8所示为带有初弯曲桁架单元的变形。在如图所示的坐标系下,带有初弯曲的桁架单元只能传递轴向荷载。在目前的研究中,通常假定构件的轴线形状半正弦曲线,如式(2—11)所示:

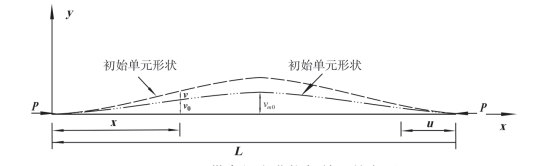
图2-8 带有初弯曲桁架单元的变形
式中v0是沿构件轴向x坐标位置处的初弯曲值,vm0是构件跨中位置处的初始弯曲的幅值,L是含缺陷桁架单元的原始长度。假设在轴向力P作用下,构件的侧向变形为v,则可得到带有初弯曲的桁架单元的平衡偏微分方程,当轴向力为压力时,平衡方程如式(2—12)所示。
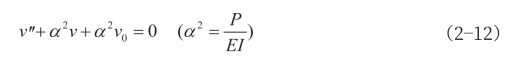
式中E为构件材料弹性模量,I是构件横截面的惯性矩。式(2—12)的边界条件可如式(2—13)所示。
![]()
则式(2—12)的解可以如式(2—14)所示。

由轴向荷载和二阶效应引起的构件轴向变形,ΔL,可以通过式(2—15)计算得到。
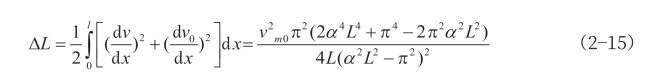
则轴向力和轴向变形之间的平衡方程可如式(2—16)所示。

式中u是图2—8所示的名义轴向变形,A是构件的横截面面积。
当桁架单元处于受拉状态时,可得到类似的推导过程。在该情况下,式(2—15)和(2—16)可以被改写为式(2—17)和(2—18)。
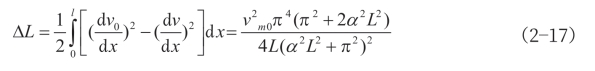
![]()
图2—9所示为长5m的桁架单元在不同的初弯曲幅值下的轴向刚度变化曲线。从图中可以看出,构件的初始缺陷会严重影响构件的刚度。这也将会严重影响网壳结构的稳定承载能力,因此应该在结构设计阶段充分考虑构件的初始缺陷。对于梁单元刚度矩阵的推导过程可在相关文献中查到。

图2-9 带初弯曲桁架单元荷载位移曲线
2.3.2 含有缺陷单元的数值建模方法
本节采用通用有限元软件ANSYS建立缺陷构件的有限元模型。在传统的分析计算中,通常建立直线然后对直线进行网格划分以模拟网壳结构中的构件。在这种情况下,不能考虑构件的初始弯曲缺陷。在该研究中,将采用以“BSPLIN”命令建立的曲线代替原来的直线来考虑构件的初弯曲。在构件的跨中位置设定初弯曲的幅值。在多数研究中,通常假定构件的初弯曲为半正弦曲线形状。这种线型可通过设置除了跨中位置以外的点的初始缺陷值,然后通过这些点建立B—样条曲线来逐渐逼近,如图2—10所示。为了方便设定初始缺陷的值,在每个构件位置建立局部坐标系,局部坐标系的x轴方向为构件的轴线方向,局部坐标系的y轴方向为竖直向上。构件轴线上任意一点的初始缺陷值可通过ANSYS中内置的正弦函数获得。通过循环语句,可以对结构的每个构件施加初始缺陷。整个过程操作起来简便快捷且易被工程人员掌握。(https://www.xing528.com)
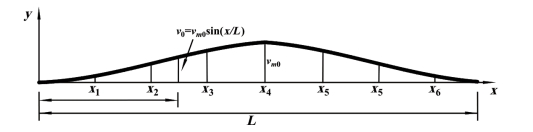
图2-10 缺陷构件及局部坐标系
2.3.3 数值验证
2.3.3.1 双构件结构
为了验证本文所提出的构件缺陷单元的数值建模方法的有效性,本节对双构件结构进行了分析计算。具有不同矢高的双构件结构是一种非常流行的算例结构。如图2—11所示,本文对矢高为0.025m,跨度为1m的双构件结构进行了分析,假定构件的初始缺陷幅值介于0~2%的构件长度之间变化。在本算例中,只设置构件跨中位置处的初始弯曲值。将计算结果与Chan 和Zhou所得结果进行对比。
图2—12所示为将构件的初弯曲幅值设置为不同值时所得到的荷载位移曲线,并与已有研究的对比结果。从图中可以看出,构件的初弯曲幅值严重影响双构件结构的稳定极限荷载。这是由于初弯曲导致的P—δ效应。通过比较可知,本文所得结果与Chan和Zhou所得结果完全吻合。本文所提出的构建缺陷构件的方法的精确性与可靠性得到了验证,同时也证明,仅在构件跨中位置指定初始缺陷值就可以保证计算精度。
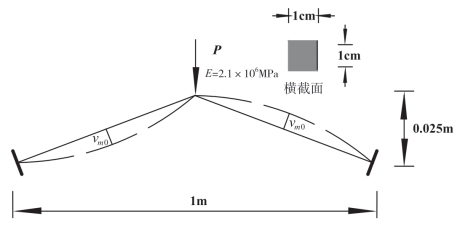
图2-11 双构件结构示意图
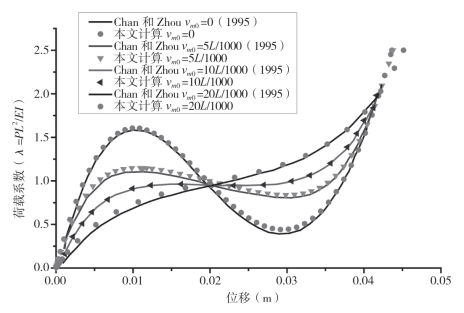
图2-12 双构件结构的荷载位移曲线
由前述方法可知,缺陷构件通过在有限元软件中建立曲线几何模型来代替,然后对曲线进行网格划分。若以较少的单元对曲线进行划分,则会出现折线代替曲线的情况,会给计算结果带来误差。为了能较好地反映构件的弯曲线型,应将构件划分足够的单元。本节对构件应划分的最少单元数以保证计算结果精度进行了研究。将双构件结构的构件以不同的单元数进行划分,并将结果进行对比,如图2—13所示。由计算结果可知,当将构件划分为两个单元时,计算结果会严重偏离,在该情况下,构件会成为折线梁。当构件划分单元的数量超过10的时候,计算结果将不会再随着单元数量的增加而增加。由此可得出结论,当构件划分的单元数量超过10时,即可以保证计算精度。
2.3.3.2 铰接星形穹顶
本节采用上述建立缺陷构件的方法建立了星形穹顶的有限元模型,并进行了非线性稳定性分析。星形穹顶的构件都是铰接连接。本文首先采用BEAM188单元进行网格划分,建立有限元模型,然后通过“ENDRELEASE”命令将刚接节点转变为铰接节点。星形穹顶的几何示意图和构件的截面特性如图2—14所示。
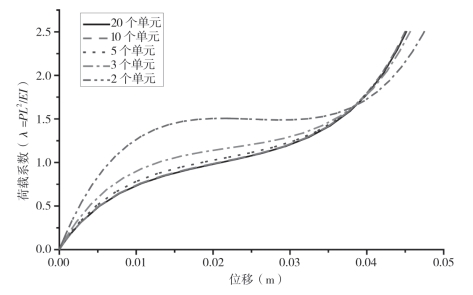
图2-13 划分不同单元数所得结果对比
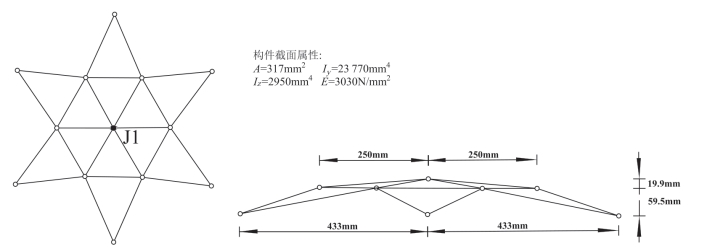
图2-14 星形穹顶的几何示意图和构件的截面特性
图2—15所示为包含构件缺陷的结构有限元模型。为对比研究,分别将构件的缺陷在水平方向、竖直方向和同时两个方向均施加3种情况。每个构件被划分为10个单元。从操作过程可以看出,本文所提方法可以简单有效地施加构件的缺陷。
图2—16所示为计算得到的荷载位移曲线。从图中可以看出,不同方向的构件初弯曲会不同程度地降低结构的稳定承载能力。通过对比图2—16(a)和(b)可以看出,对本结构来说,水平面内的构件初弯曲对结构稳定承载能力的影响要大于竖直面内的构件初弯曲。当构件的初弯曲幅值设定为20L/1000时,结构的稳定承载力降为原来的67%。从图2—16(c)可以看出,两个方向均存在初弯曲的结构,稳定承载能力会更低。
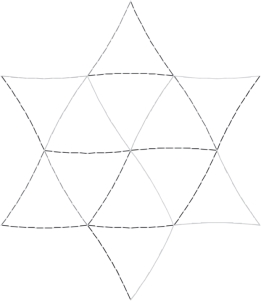
图2-15 缺陷结构有限元模型

图2-16 不同缺陷方向和幅值的结果对比
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




