近年来,有关节点刚度及节点刚度对整体结构力学性能影响的研究引起了众多学者及工程师的注意,同时也取得了很多具有应用价值的结果。但是直至目前,还没有能在通用有限元软件中考虑节点半刚性的简单有效的方法。为克服目前的局限,本文提出了简化的考虑节点半刚性的有限元建模方法。
该方法假定结构的每个构件由两个单元组成:只有抗弯刚度和抗扭刚度的梁单元和只有轴向刚度的梁单元(等价于杆单元)。
等截面梁在弯矩M作用下的转角,如图2—2所示,可以通过式(2—1)计算得到,然后梁单元的抗弯刚度可通过式(2—2)得到。
研究表明,节点刚度对网壳的力学行为有至关重要的影响,尤其是对于网壳结构的稳定性。在传统的有限元模型中,节点通常被假定为刚接或者铰接。事实上,几乎所有的节点都表现出半刚性的力学特性。对于该类结构,半刚性节点可通过弹簧单元替代,如图2—1(a)所示。梁—弹簧单元在弯矩M作用下的转角可通过式(2—3)得到。梁单元的抗弯刚度可通过式(2—4)得到,该式表明,如果弹簧刚度足够大,则式(2—4)与式(2—2)等效。
Lo’pez提出采用位于钢管和球节点之间的弹塑性柱体来模拟螺栓的作用,由于网格结构会包含很多个构件,因此若采用该方法建立有限元模型,既浪费时间又浪费精力。基于此,本文提出了考虑节点刚度的双单元法,如图2—1(b)所示。该方法假定结构的每个构件由两个单元组成:只有抗弯刚度和抗扭刚度的梁单元和只有轴向刚度的梁单元。
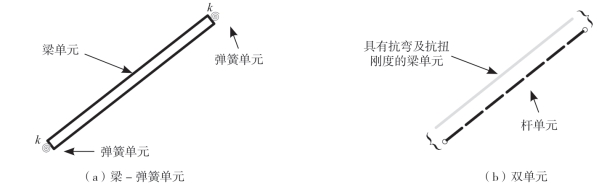
图2-1 考虑节点刚度的数值模型
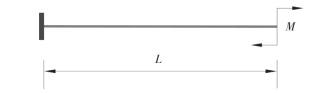
图2-2 弯矩作用下的梁单元
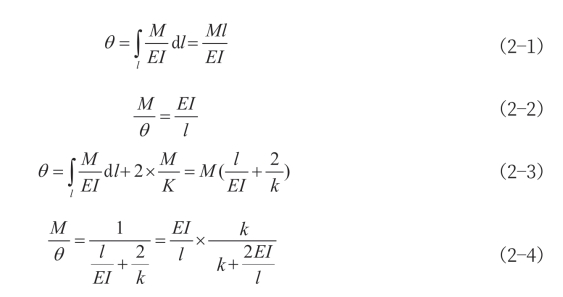
式中θ是梁单元在弯矩作用下的转角;I是构件截面惯性矩;E=206GPa是材料弹性模量;k是弹簧单元的抗弯刚度。
假定α为整个梁节点体系的整体刚度系数,β是只考虑节点刚度的刚度系数,如式(2—5)和式(2—6)所示。由式(2—5)和式(2—6)可得到α和β之间的关系,如式(2—7)所示。为形象地表示α和β之间的对应关系,将α和β之间的关系以曲线表示,如图2—3所示。从图中可以看出,随着节点刚度系数β的增大,整体的刚度系数趋近于1。

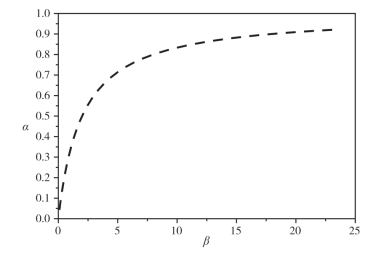
图2-3 α和β的对应曲线
采用通用有限元软件进行计算获得结构的荷载位移曲线。首先采用普通梁单元(BEAM4)建立双构件结构的有限元模型。BEAM4单元是具有轴向拉压、受弯、受扭能力的两节点线性单元。该单元每个节点具有6个自由度:沿x、y和z方向的平移自由度和绕x、y和z轴的扭转自由度。BEAM4单元在荷载作用下的平衡方程以及单元刚度矩阵如式(2—8)所示。(https://www.xing528.com)

式中A、E、L、G和J分别是构件横截面面积、弹性模量、构件长度、剪切模量和截面扭转惯性矩。
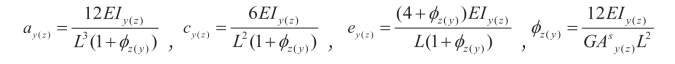
Ii是绕i轴的惯性矩,![]() 是垂直于y(z)的剪切面积。
是垂直于y(z)的剪切面积。
对于双单元中只有抗弯刚度的梁单元,采用实常数只赋予梁的抗弯刚度。该单元的刚度矩阵及在荷载作用下的平衡方程如式(2—9)所示。对于只有轴向刚度的梁单元,仍可采用BEAM4模拟,但抗弯刚度被赋予一个非常小的值,以至于该单元的抗弯刚度可以被忽略,此时该单元可以被认为是杆单元。该单元的刚度矩阵及在荷载作用下的平衡方程如式(2—10)所示。

由于双单元中的两个单元共节点,因此两个单元在荷载作用下的位移矢量彼此相等。所以式(2—8)等于式(2—9)加上式(2—10)。由于双单元中的梁单元只包含抗弯刚度,因此可以很方便地调节刚度系数以考虑节点的半刚性。
为了验证本文所提出的双单元的有效性,通过双构件结构进行验证(图2—4)。将构件的截面面积和惯性矩通过实常数输入,构件截面面积为A=0.004 8m2,截面惯性矩为I=6.28×10-6m4,将具有抗弯刚度梁单元的面积赋予一个很小以至于忽略的值。
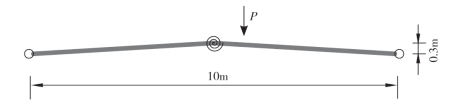
图2-4 具有半刚性节点的双构件结构
图2—5所示为通过普通梁单元和双单元得到的荷载位移曲线。从图中可以看出,两种单元所得结果完全吻合,证实了双单元的有效性。图2—6所示为具有不同抗弯刚度系数的双构件结构的荷载位移曲线。从图中可以看出,双构件结构的节点刚度对极值荷载有很大影响。计算结果同时也表明,通过梁单元的抗弯刚度系数α考虑节点半刚性是可行的。
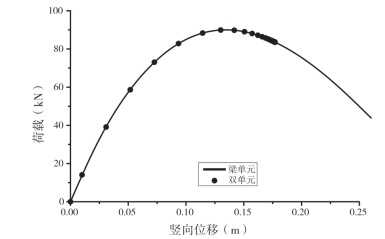
图2-5 普通梁单元与双单元所得结果对比
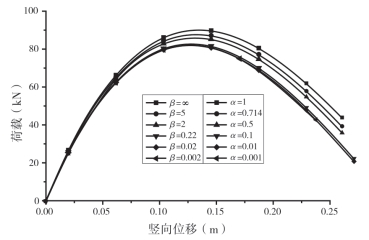
图2-6 不同抗弯刚度系数所得荷载位移曲线
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




