【摘要】:根据最大流最小截集定理,在任一网络中,最大流的流量等于最小截集的容量[71-73],即最小截集是网络的“咽喉要道”或“卡脖子的地方”,要想增加网络的最大流的流量,必须增加最小截集中弧的容量[72]。求解网络最大流目前最常用的便是标号算法,这种算法由Ford和Fulkserson于1956年提出,故又称Ford-Fulkserson算法,该算法其实质是判断是否有增广链存在,并设法把增广链找出来[71]。图3-15容量网络示意图
根据最大流最小截集定理,在任一网络中,最大流的流量等于最小截集的容量[71-73],即最小截集是网络的“咽喉要道”或“卡脖子的地方”,要想增加网络的最大流的流量,必须增加最小截集中弧的容量[72]。
求解网络最大流目前最常用的便是标号算法,这种算法由Ford和Fulkserson于1956年提出,故又称Ford-Fulkserson算法,该算法其实质是判断是否有增广链存在,并设法把增广链找出来[71]。
Ford-Fulkserson算法的实现可采用已有的MATLAB程序[64],其具体代码如下:
function[f wf No]=fofuf(C,f1)
% C表示弧上的容量
% f1表示弧上现在的流量函数,默认情况下为0
% f表示最大流
% wf表示最大流量(https://www.xing528.com)
% No标点函数,由此可得最小割
%注:待求最大流的源为第一个顶点,汇为最后一个顶点


以上程序在具体应用时要求先输入网络容量矩阵C,如图7所示,其容量矩阵C=[0 2 2 0 1 0;0 0 0 2 0 0;0 0 0 1 0 0;0 0 0 0 1 1;0 0 0 1 0 3;0 0 0 0 0 0]。
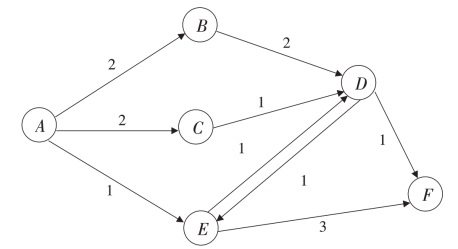
图3-15 容量网络示意图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




