交通工程应用:ANP法与D-S证据理论融合算法简介

2.3.2.1 ANP法简介

（1）网络层次分析法（QNP法）的产生背景

层次分析模型是Thomas L.Saaty[50]在1971年提出的，主要应用在不确定情况下及具有多个评估准则的决策问题上。在问题求解的过程中，AHP法假设每一阶层的要素均需相互独立（independence），并将复杂的问题系统化（systematize）以进行评估。然而，现实生活中的问题时常存在相依（dependence）或回馈（feed back）关系，随着问题愈大，关系也愈错综复杂，此时若再使用独立性的假设，则有可能过度简化问题，致使评估结果产生偏差。

为避免上述缺点，Saaty于1996年正式提出考虑相依及回馈关系的层次分析法——网络层次分析法（Analytic Network Process，ANP）[51]。网络层次分析法的架构以网络图形方式表达，包括控制层和网络层两部分，其中控制层是指准则与次准则之间的网络关系，它影响着系统之间的内部关系，而网络层则主要描述影响每个决策准则的元素（element）与决策准则的群组（clusters）之间的网络关系，见图2-13。可以发现，在网络层次分析法的假设中，允许同一及不同的决策准则间，各元素彼此相依或回馈。倘若同一决策准则间，元素彼此相依或回馈，称之为内部相依（inner dependence），而若不同决策准则间的元素彼此相依或回馈，则称为外部相依（outer dependence）。这种允许准则间可以相依或回馈的假设，较能符合现实决策中遇到复杂问题的实际状况，尤其是当决策时还必须面临不确定性及风险等的考虑时。而除了图形表示外，在实际做法上，网络层次分析法提供比例尺度（ratio scale）让决策者将其判断及对决策准则的衡量标准输入，再根据其输入的比例得到整个决策准则体系中各准则的权重。换言之，网络层次分析法提供了一个完整的架构，使得网络内部的元素所在的群组能够以任何方式相联结，然后再进一步地以数值尺度转换为比例尺度的方法得出元素和元素间及群组和群组间相互影响的权重大小。

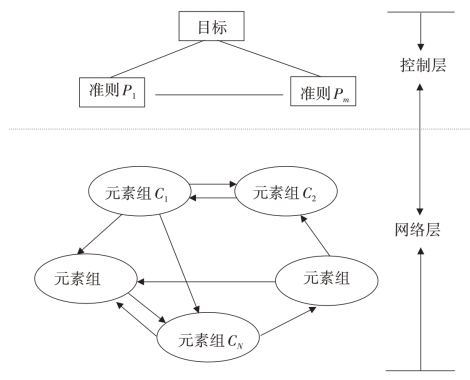
图2-13　典型的ANP结构

（2）网络层次分析法建模步骤

步骤1建立问题的网络层级架构

依照问题特性确定目标为何，并寻找决策准则（criteria）与各准则群组所包含的次准则（sub-criteria），寻找各准则之间的相互影响性，若有相互影响即为外部相依（outer dependence），若各准则群组所包含的次准则（sub-criteria）彼此相互影响，则为内部相依（inner dependence），由此绘制出决策问题的网络层级架构。

步骤2 ANP问卷设计与填写（即进行各决策准则成对比较）

成对比较针对两两准则进行比较，比较可分为两部分，包括各准则间成对比较与准则群组内次准则之间相互比较。次准则的成对比较又分为同一群组间的成对比较与不同群组元素成对比较（比较评估尺度与AHP法相同）。根据Saaty（1980）建议[52]，一般采用专家问卷法进行各决策准则成对比较以及相关重要性评判。问卷中重要性等级分为对称的五个等级，分别为非常重要、很重要、比较重要、稍微重要以及同等重要，而各主要等级间，再进一步细分折中，让填卷者在两主要等级间再进行考虑。尺度由左而右分别为{9，8，7，6，5，4，3，2，1，2，3，4，5，6，7，8，9}，尺度说明见表2-4。

表2-4　ANP评分标度的含义

注：若因素i与j比较得aij，则因素j与i比较的判断应为1/aij。

步骤3建立成对比较矩阵

根据专家评估，即可得到成对比较矩阵。ANP的成对比较矩阵可分为外部关系及内部关系，外部关系之比较在于为判断同一层级的准则达到上层目标的重要性或优越性的特征向量值，内部关系之比较在于为判断某一准则受内部其他准则影响的重要性或优越性的特征向量值。根据Saaty（1980）[50]的建议，若成对比较矩阵A为n×n矩阵，则只需计算n×(n-1)/2个评比值，分别对评估因子Ai与Aj（i，j=1，2，3，…，n，i≠j）进行两两比较，则可得到以下的成对比较矩阵A。

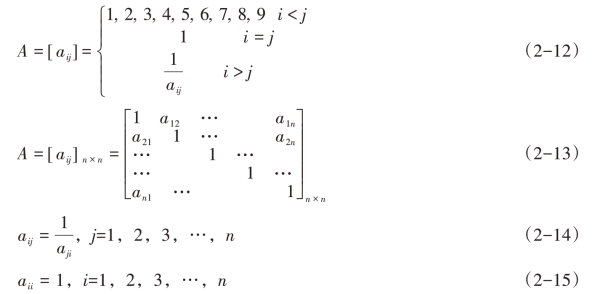
步骤4层次单排序及一致性检验

层次单排序是确定下层各因素对上层某因素影响程度的过程。对每个成对比较矩阵计算最大特征值及其对应的特征向量，经归一化后即为同一层次相应因素对于上一层次某因素相对重要性的排序权值。

衡量一个成对比较矩阵（n＞1阶方阵）不一致程度的指标为CI：

其中λmax是成对比较矩阵的最大特征值。

一致性指标CI的值越大，表明判断矩阵偏离完全一致性的程度越大，CI的值越小，表明判断矩阵越接近于完全一致性。一般判断矩阵的阶数n越大，人为造成的偏离完全一致性指标CI的值便越大；n越小，人为造成的偏离完全一致性指标CI的值便越小。

判断矩阵一致性指标CI与同阶平均随机一致性指标RI（Random Index）之比称为随机一致性比率CR（Consistency Ratio）。

式中，RI为平均随机一致性指标，表2-5给出了1～9阶正互反矩阵计算500次得到的平均随机一致性指标。

表2-5　平均随机一致性指标

当CR＜0.10时，便认为判断矩阵具有可以接受的一致性。当CR≥0.10时，就需要调整和修正判断矩阵，使其满足CR＜0.10，从而具有满意的一致性。

步骤5超级矩阵运算

为了处理评估因子外部和内部两种相依关系，ANP法在计算权重时采用一种特殊的矩阵结构——超级矩阵。超级矩阵是由许多子矩阵所组成，子矩阵即步骤4所得到的成对比较矩阵中所计算的最大特征值λmax。若评估因子在问卷中显现无相关者，则子矩阵的成对比较值为0。以图2-14中之范例为例，A因素与B因素呈外部相依关系，且A因素与B因素各呈内部相依关系，其超级矩阵可表示为：

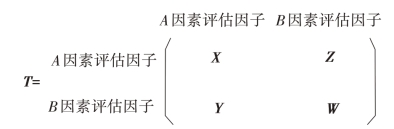
图2-14　问题架构范例图

矩阵X：表示在A因素影响下，A因素内的各评估因子的成对比较矩阵。

矩阵Y：表示在A因素影响下，A因素的各评估因子与B因素的各评估因子的成对比较矩阵。

矩阵Z：表示在B因素影响下，A因素的各评估因子与B因素的各评估因子的成对比较矩阵。

矩阵W：表示在B因素影响下，B因素内的各评估因子的成对比较矩阵。

其中T为未加权超级矩阵（Unweighted super Matrix），因为矩阵中的行列值不符合随机原则，所以必须经过加权转换。分别再乘上成对比较矩阵所求得最大特征值进行矩阵运算，即可得到加权超级矩阵。

超级矩阵的行向量总和等于1时，才能符合随机原则。其中行向量不等于1，假设矩阵X与矩阵Z乘以0.3再加上矩阵Y与矩阵W乘以0.7之后，它的行向量加总将为1，因此已加权的超级矩阵如图2-15所示。

图2-15　问题架构范例图

再经极限化过程，即将加权超级矩阵多次相乘之后，相依关系将逐渐收敛而得到一个固定的收敛值，且极限值将固定不变，如此可得到各评估因子的整体相对权重。

步骤6汇整评估因子权重

将经过超级矩阵极限化运算整合后所得到的评估因子的相对权重汇整，即完成问题架构下各评估因子间相对的重要程度。

（3）Super Decisions软件简介

Super Decisions软件是由Saaty和他的研究团队共同研发完成的，该软件主要用来计算具有相依及回馈的决策问题。它除了可以用在网络层次分析（ANP）法的计算之外，也可以应用在层次分析（AHP）法的运算。Super Decisions软件的研发，让决策者可以很轻松地针对问题进行分析，省去了运算时间，决策者只需架构出该问题的网络层，在无须理清图形的形态下，也不需计算繁复的极限化超级矩阵，即可计算出极限化之超级矩阵，使得问题解决更有效率。经过极限化后，在考虑各因子间的相互关系并自动成对比较矩阵进行一致性检验后，可求得该因子在整体结构中的相对权重，因此，运用Super Decisions软件来帮助解决繁杂的计算。此外，该软件提供了人性化的操作对话框，让执行者很快完成比对矩阵的动作，也有彩色对象供用户丰富网络层的页面，如图2-16所示。

图2-16　Super Decisions软件界面

（4）用ANP法对GD-AHP法进行改进

应用ANP法对GD-AHP法进行改进，目的是使建立的评价指标体系以及指标体系中的各个指标间的相互关系更加符合实际情况，使得各指标相对于目标的权重确定更加合理可信。

2.3.2.2 D-S证据理论及其融合算法简介

（1）D-S证据理论

Dempster-Shafer方法（简称D-S方法）是利用证据理论所得到的不确定性推理方法，目前已经广泛运用于机器人智能导航系统、医疗诊断系统、故障诊断系统等等。证据理论是Dempster于1967年提出的[53]，他的学生Shafer[54]于1976年对其进行了发展。在证据理论中最基本的概念是信任测度与似然测度，它依据可信度（belief）函数运算。Dempster-Shafer模型具有利用证据积累以缩小假设集合的重要能力，在区分不确定与不知道及精确反映证据收集过程等方面显示了很大的灵活性。

Dempster-Shafe理论讨论一个“识别框架”Θ，它是关于命题的相互独立的可能答案或假设的集合。对于某个事件的肯定与否定不是简单的真与伪的判断，而是有测度的。肯定与否定的合成测度叫作置信度；置信度不是概率也不是肯定与否定的简单合成。这种带有测度的肯定度与否定度构成了证据理论的一个独特属性[55]。

（2）有关概念

定义1设Θ为识别框架，如果集函数m:2Θ→[0,1]（2Θ为Θ幂集，它是所有子集的集合）满足：

此时m称为识别框架Θ上的基本可信度分配，又称为mass函数。

定义2设：Bel：2Θ→［0，1］为Θ上的一个信任函数，定义：pl：2Θ→［0，1］，pl(A)=1-Bel称pl为Bel的似真函数。pl(A)称为A的似真度或者说是发现A可靠或似真的程度。

根据定义2可以用与Bel对应的m重新来表示pl(A)：

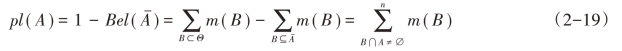
（3）合成法则

Dempster-Shafer证据理论合成法则是为了同时利用来自相互独立的不同信息源两组或多组证据，提高对时间的置信度而提出的一种多信息的组合法则。

定义3设Bel1和Bel2是同一识别框架Θ上的两个信度函数，m1和m2分别是其对应的基本可信度分配，m1和m2的焦元［若A⊆Θ且m(A)＞0，则称A为焦元］分别为A1，A2，…，Ak和B1，B2，…，Bl，设

那么，由式（2-20）定义的函数m：2Θ→［0，1］是基本可信度分配

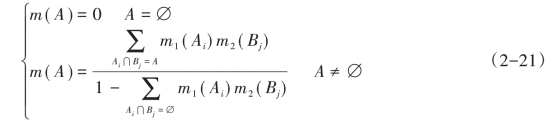
记k=则上式变为：

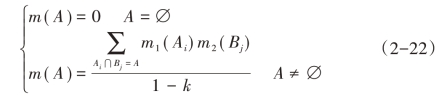
多个信度函数的组合规则为：

定理1设Bel1，Bel2，…，Beln是同一识别框架Θ上的信度函数，m1，m2，…，mn分别是其对基本可信度分配，如Bel1，Bel2，…，Beln存在且基本信度分配为m，则n个信任函数的组合为Bel1⊕Bel2⊕…⊕Beln，⊕为直和，由组合证据获得的最终证据与其次序无关。

下面给一个例子说明Dempster-Shafer合成法则的应用：

两组证据初始信度分配为：

m1(A)=0.4 m1(B)=0.3 m1(C)=0.3

m2(A)=0.35 m2(B)=0.2 m2(C)=0.45

用Dempster-Shafer法则合成可以得到：

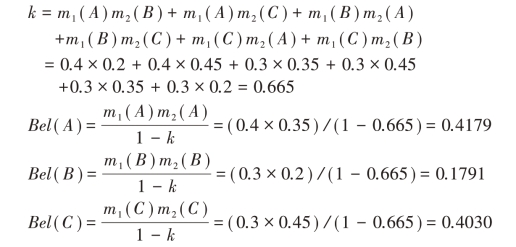
（4）用D-S证据理论融合算法对GD-AHP法进行改进

利用D-S证据理论融合算法将各个专家确定的相对权重进行综合，可实现多个专家意见的有效融合，比起以往的综合方法更可信。用D-S证据理论融合算法融合多个专家确定的相对权重的关键在于：将每位专家确定的底层指标元素对于顶层目标的权重等同于D-S证据理论中的可信度。

2.3.2.3基于ANP法的高速公路隧道火灾风险评价模型(www.xing528.com)

（1）指标的选择与确定

1）指标选取原则

评价指标体系的制定是一个很困难的问题。一般来说，指标范围越宽，指标数量越多，则方案之间的差异越明显，有利于判断和评价，但确定指标的大类和指标的重要程度也越困难，处理和建模过程也越复杂，因而歪曲方案的本质特性的可能性也越大。评价指标体系要全面地反映出所要评价的系统的各项目标要求，尽可能地做到科学、合理，且符合实际情况，并基本上能为有关人员和部门所接受。建立评价指标体系时一般应遵循以下原则：

①系统性原则

选取的评价指标应该囊括高速公路隧道火灾安全系统中的各组成部分，并把它们有机地联系起来，力求全面、客观地反映指标之间的关系和层次结构。因此，指标的选择不是简单的指标的罗列和堆砌，更应考虑指标间的系统关系。应该利用网络层次分析法的基本思想将其分为目标层、准则层、指标层，从而使指标体系成为一个有机的统一体。

②指标的可测性原则

选取的指标必须满足可测量的要求，才能在指标体系建立之后有一个客观的测评依据。

③可操作性和实用性原则

评价指标应该含义明确，收集评价指标数据、资料方便，便于统计和量化计算。指标值能准确、快速获取且方法易于掌握。

④科学性和可靠性原则

评价标准和理论必须建立在科学的基础上，才能反映客观实际并对实践具有指导作用，评价指标必须可靠、起实际作用，才能构成评价标准的基础，如果指标本身很不可靠，那么评价标准就失去了意义。

2）指标选择与确定

在遵循指标选取原则的基础上，根据国内外关于高速公路隧道火灾风险评价指标体系方面的研究成果，最终建立高速公路隧道火灾风险评价的指标体系，如图2-17所示。由图2-17可知，影响高速公路隧道火灾发生概率和严重程度的风险因子主要有8项：隧道长度（C1）、隧道纵坡（C2）、隧道类型（C3）、车道宽度（C4）、其他项（C5）、交通量（C6）、大型车比例（C7）以及危险品运输管理（C8）。

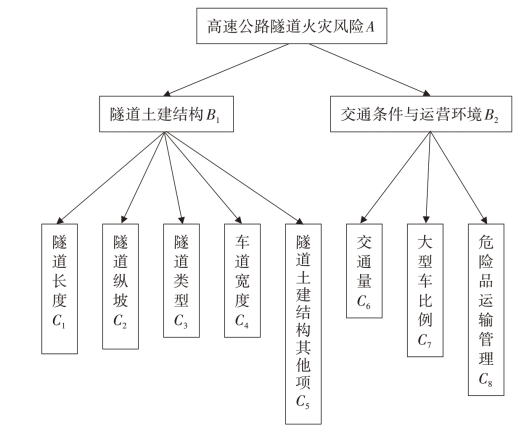
图2-17　高速公路隧道火灾风险评价指标体系

3）指标介绍及量化

①隧道长度（C1）

隧道长度指进、出口洞门端墙墙面之间的距离，即两端墙墙面与路面的交线同路线中线交点间的距离。公路隧道长度越大，同一时刻行驶在隧道中的车辆就越多，隧道环境中存在的风险就越大，驾驶员的心理、生理压力也越大。表2-6为我国《公路隧道设计规范》中规定的按隧道长度对隧道进行分类的标准。建议我国高速公路隧道长度的风险评分值，按照表2-7和图2-18取值。

表2-6　公路隧道按长度分类标准

表2-7　公路隧道按长度风险评分表

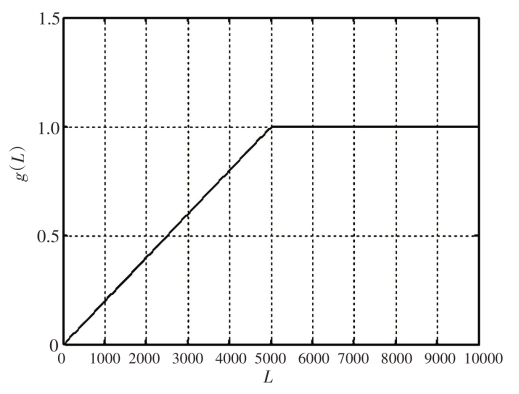
图2-18　隧道长度火灾风险评分图

②隧道纵坡（C2）

隧道的纵坡是反映隧道纵向线形的主要指标，在对隧道进行评价时，可以通过查找被评价隧道相关的设计资料获得。

对于公路隧道的纵坡，我国《公路隧道设计规范》（JTG D70—2004）规定为不小于0.3%和不大于3.0%。2002年邱豪磊翻译的《欧洲公路隧道风险评分表》中的《隧道纵坡风险换算表》见表2-8，根据表2-8给出的纵坡与风险分数之间的关系进行线性回归，可得回归方程，如图2-19和式（2-23）所示。由公式（2-23）计算可得，当隧道纵坡为0.3%时，其风险分数为0.049；当隧道纵坡为3%时，其风险分数为2.554。当高速公路隧道纵坡C2＜0.3%时，其火灾风险评分值为0；当0.3%≤C2≤3%时，其火灾风险评分值应按照式（2-23）计算求得；当C2＞3%时，其风险评分值为3。

表2-8　隧道纵坡风险评分表[56]

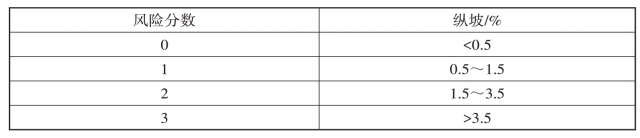
注：①坡度为纵向最大坡度；

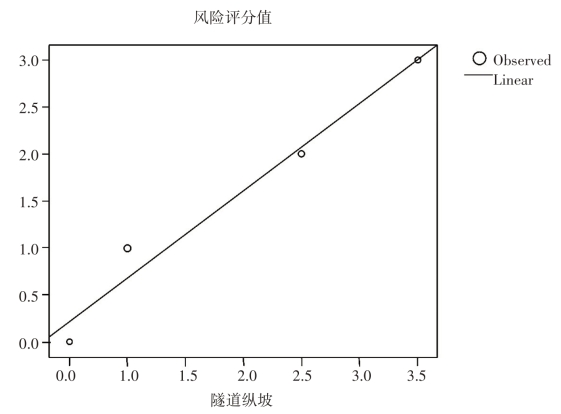
图2-19　隧道纵坡风险评分图

③隧道类型（C3）

随着经济社会的发展、科学技术的进步，公路隧道建设强度的加大，越江跨海隧道越来越多。据有关资料显示，在最近的20～30年内，我国将建设5条跨海隧道，其中包括渤海湾跨海隧道、杭州湾跨海隧道、琼州海峡跨海隧道、台湾海峡跨海隧道等[57]。公路越江跨海隧道建筑结构复杂，环境相对密闭，一旦发生火灾，后果将不堪设想。基于以上考虑，引入隧道类型风险指标，主要用来判别隧道属于山岭隧道还是水下隧道。对于隧道类型的安全评分标准，在咨询相关专家的基础上建议参照表2-9进行。

表2-9　隧道类型风险评分标准

④车道宽度（C4）

一般来说，较宽的路面有利于行车安全，道路交通事故率（AR）随路面宽度的增加而降低。图2-20为美国双车道公路事故率（AR）与路面宽度的影响关系[58]。总体来看，AR与路面宽度基本上呈线性关系，路面越宽，AR越小。对于公路隧道，路面宽度对事故率的影响与一般公路相类似。由图2-20可得到路面宽度（w）与事故率之间的关系式，如式（2-24）所示。结合我国高速公路隧道的具体情况，由式（2-24）计算可得：当隧道路面宽度为3.5 m（3.5 m×1）时，其风险得分为2.857；当隧道路面宽度为11.25 m（3.75 m×3）时，其风险得分为0.643。所以，建议我国高速公路隧道路面宽度的风险得分按照式（2-24）计算得到。根据以上分析可得，其值应该介于［0.643，2.857］之间。

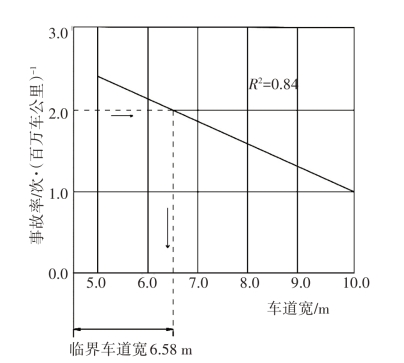
图2-20　双车道公路事故率与路面宽度的影响关系

⑤隧道土建结构其他项（C5）

隧道土建结构其他项主要考虑隧道中是否有车道合并、是否有交叉路口和是否有陡坡区段，其风险评分可参照表2-10进行。

表2-10　隧道土建结构其他项评分对照表[59]

⑥交通量（C6）

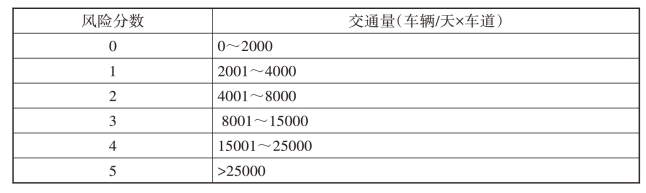
交通量是指在指定时间内通过道路某地点或某断面的车辆、行人数量，可分为机动车交通量、非机动车交通量及行人交通量等。不特别说明时，交通量一般是指机动车交通量，以小时、日或年计算。由于高速公路隧道大都处于山区或偏远地区，因此，高速公路隧道火灾风险评价中的交通量指机动车交通量。交通量指标对应的风险评分标准见表2-11[49]（参考欧洲EuroTAP计划中的评分标准）。

表2-11　交通量评分对照表[59]

⑦大型车比例（C7）

一般来说，车型比例与事故率之间呈现出一种近似抛物线的发展趋势。当小型车比例大于80%时，即交通组成以小型车为主时，交通流趋于稳定，同样事故率也趋于稳定；当小型车比例小于80%且大于20%时，此时交通组成比较复杂，大型车与小型车之间的相互摩擦增大，交通参数离散程度大，事故率增大；当小型车比例小于20%，即大型车比例大于80%时，交通组成以大型车为主，交通流再次趋于稳定，使原本分布比例比较离散的交通参数趋于均匀，相应地事故率也趋于稳定。大型车比例风险评分如表2-12所示[60]。

表2-12　大型车比例评分对照表[60]

⑧危险物品运输管理（C8）

危险品运输直接影响着高速公路隧道中火灾发生的概率和严重程度，对于高速公路隧道危险品运输管理的风险评分，建议参照表2-13进行。

表2-13　危险物品运送评分对照表[59]

4）指标风险评分的标准化处理

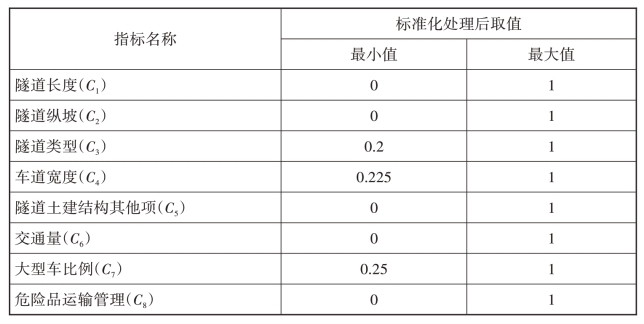
考虑到各风险因素评分值区间的不同，用式（2-25）对各风险因子的评分值进行标准化处理，使其评分最终都介于[0，1]之间，如表2-14所示。

表2-14　各指标风险评分标准化值

（2）指标间相互影响关系分析

根据确定的高速公路隧道火灾风险评价指标体系及风险参数表可知：

1）高速公路隧道火灾风险（A）主要由隧道长度（C1）、隧道纵坡（C2）、隧道类型（C3）、车道宽度（C4）、隧道土建结构其他项（C5）、交通量（C6）、大型车比例（C7）以及危险品运输管理（C8）等8项风险参数所决定；

2）8项主要风险参数之间并不是彼此独立的，主要表现在以下几个方面：

①对风险参数隧道纵坡（C2）有影响的风险参数为：隧道长度（C1）、隧道类型（C3）、隧道土建结构其他项（C5）；

②对风险参数车道宽度（C4）有影响的风险参数为：隧道长度（C1）、隧道土建结构其他项（C5）、交通量（C6）、大型车比例（C7）；

③对风险参数交通量（C6）有影响的风险参数为：大型车比例（C7）以及危险品运输管理（C8）；

④对风险参数危险品运输管理（C8）有影响的风险参数为：隧道长度（C1）、隧道纵坡（C2）、隧道类型（C3）、车道宽度（C4）、隧道土建结构其他项（C5）、交通量（C6）、大型车比例（C7）。

8个主要风险参数之间的关系如图2-21所示。

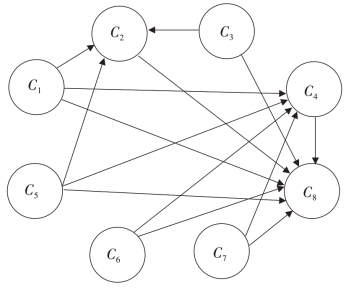
图2-21　风险因素相互关系图

（3）模型构建

根据所建立的高速公路隧道火灾风险评价体系以及各风险参数之间的关系图，在超级决算软件Super Decisions中建立相应的ANP模型，如图2-22所示。

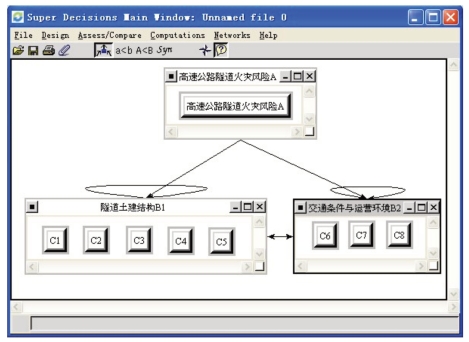
图2-22　ANP模型的软件实现界面