【摘要】：表1-2模型精度分级表
灰色系统理论是一种研究“部分信息已知、部分信息未知”的“小样本”“贫信息”不确定性问题的新方法，并依据信息覆盖，通过序列算子的作用探索事物运动的现实规律，其特点是“少数据建模”[22-25]。
1.2.1.1建模步骤
由于现场数据监测时间间隔往往是不等时距的，所以需要采用非等时距的GM（1，1）灰色预测模型把原始的非等时距时间间隔序列转换成等时间间隔序列，按等时距GM（1，1）模型进行数据处理。
假设冻土路基沉降监测数据的采集时间间隔序列（单位：d）为：
对该序列进行一次累加生成累计时间的新序列：
实测的冻土路基单次沉降量序列（单位：mm）为：
对该序列进行一次累加生成累计沉降量的新序列：
根据最小二乘法原理，可得参数列：
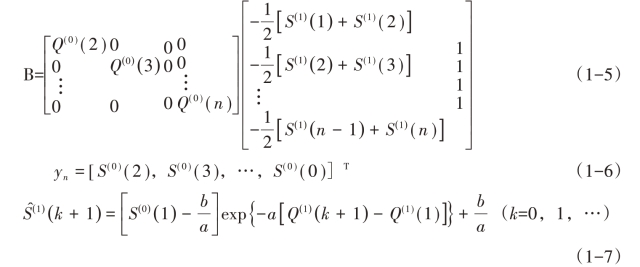
式（1-7）称为全信息的非等时距GM（1，1）模型。
1.2.1.2模型后验差检验[21,26]
（1）原始数据
原始数据的平均值为：
(www.xing528.com)
原始数据的修正方差为：
原始数据的均方差为：S1
（2）残差
预测求解后还原数列为：
残差为：
残差的平均值为：
残差的修正方差：
残差的均方差为：S2
（3）模型精度分级标准值均方差比值为：
小误差概率为：
按照C与p计算的结果，查看表1-2模型精度分级表，评定模型的精度。
表1-2 模型精度分级表
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
