汽车运用工程学：大修与更新界限判定计算法

汽车使用一段时期后，需要在更新或大修两种方案之间作出判断。可修而不修，过早更新，会因未达到折旧期而造成未折旧完的部分价值的损失。应该更新而未更新，则将增加维修费用，降低生产效率。因此，究竟进行大修还是更新，需要进行判别分析后再行决策。

确定大修或更新方案时，常采用的判别式为：

R_i+S_e＜αβK_n+S_a

式中 R_i——车辆第i次大修的费用（元）；

S_e——使用成本的损失（元）；

α——大修后运输生产率与新车运输生产率的比例；

β——大修后车辆的大修间隔里程与新车大修间隔里程的比例；

S_a——更新产生的折旧损失（元）。

其中：使用成本损失S_e的大小等于大修后车辆与新购车辆的运输成本差值乘以至下次大修期间的运输生产量（即经营损失）。

更新与大修两方案耗费之差B（元）为：

B=（I₀αβ+S_a）-（R₁+S_e）

式中 I₀——新车原值（元）。

设E_τ为大修耗费效果系数，即

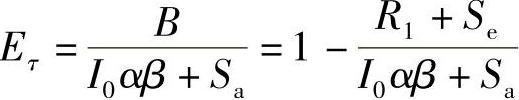
当E_τ＞0时，说明更新在经济上是合理的。

例：假定某运输公司购进的汽车的车价为I₀=14500，汽车残值为500元，单车折算吨位为3.33t（考虑实载率、里程利用率、拖挂率等因素，由统计数据求出）。该公司汽车大修次数与大修间隔里程、费用以及完好率的关系如表19-5所示，试判定在汽车进行第几次大修前进行更新最为经济。(www.xing528.com)

表19-5 汽车大修次数与大修间隔里程、费用以及完好率的关系

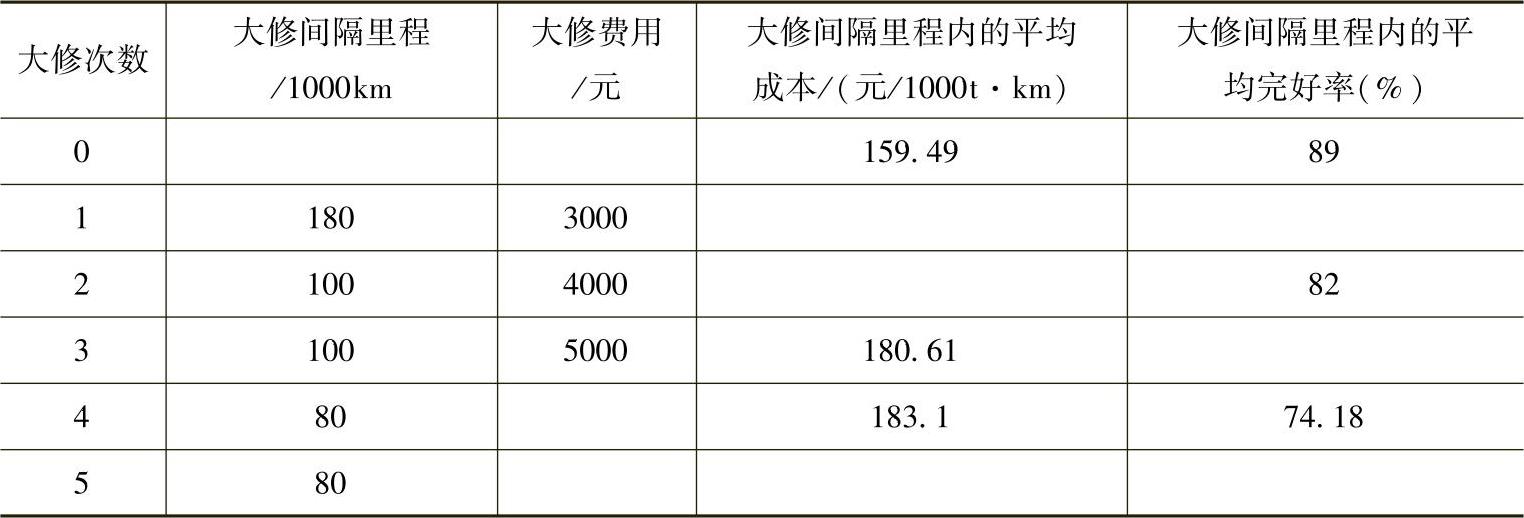
1.判定是否需要进行第三次大修

根据表19-5经计算得到：

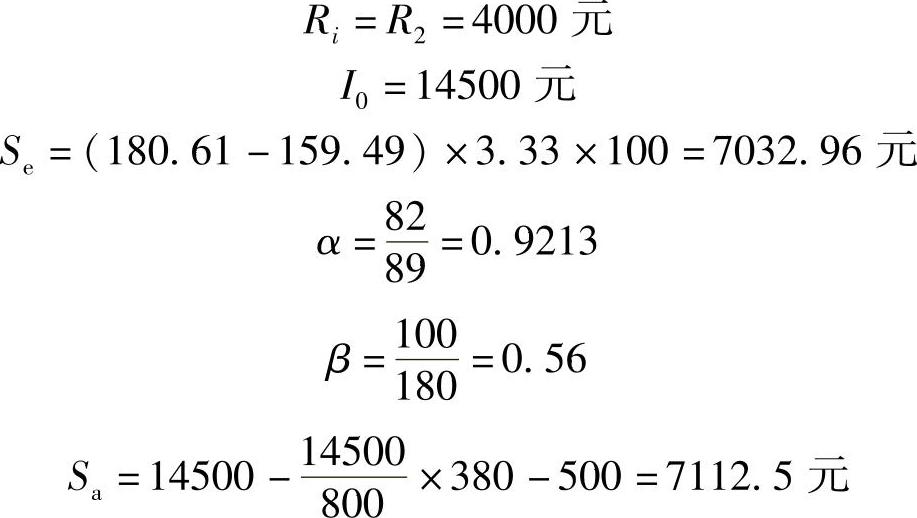
其中：折旧里程取800（1000km）。

大修耗费效果系数Eτ为：

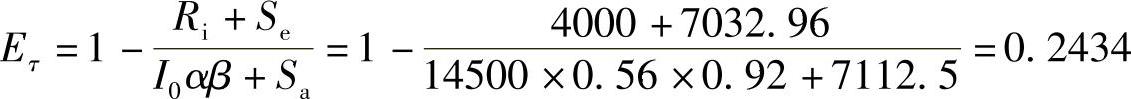
据Eτ＞0可知，进行第三次大修在经济上是合理的。

2.判断是否需要进行第四次大修

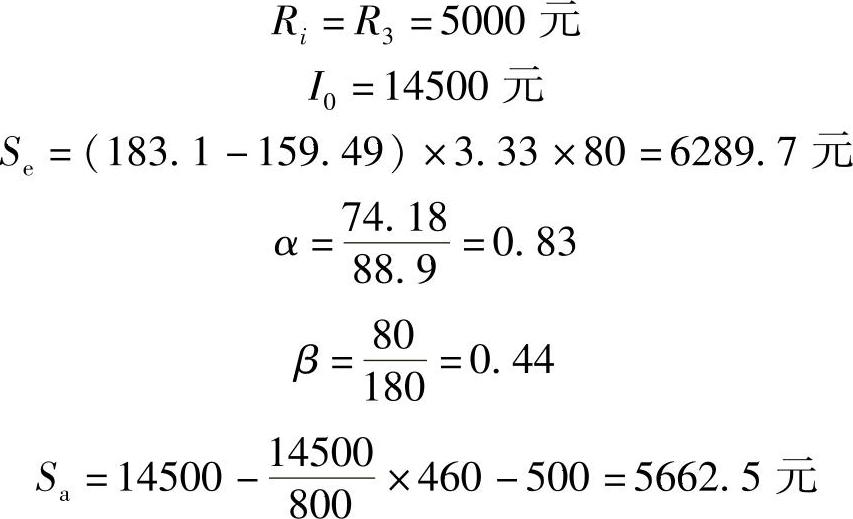
计算得大修耗费效果系数E_τ为：

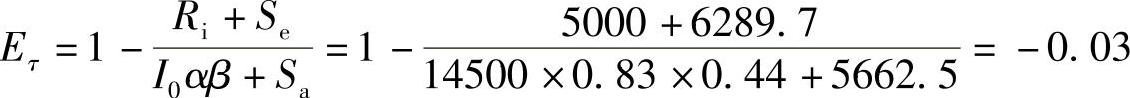
据E_τ＜0可知，进行第四次大修不经济，应在第四次大修前更新。