圆曲线测设方法：从新手到高手

（1）切线支距法。切线支距法（又称直角坐标法）是以曲线的起点ZY（对于前半曲线）或终点YZ（对于后半曲线）为坐标原点，以过曲线的起点ZY或终点YZ的切线为x轴，过原点的半径为y轴，按曲线上各点的坐标设置曲线上各点的位置。

如图7-15所示，设P_i为曲线上欲测设的点位，该点至ZY点或YZ点的弧长为l_i，φ_i为l_i所对的圆心角，R为圆曲线半径，则P_i点的坐标按下式计算

x_i=Rsinφ_i

式中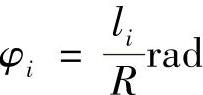

用切线支距法详细测设圆曲线时，为了避免支距过长，一般是从ZY点和YZ点分别向QZ点施测，测设步骤如下：

1）从ZY点（或YZ点）用钢尺或皮尺沿切线方向量取P_i点的横坐标x_i，得垂足点N_i。

图7-15 切线支距法详细测设圆曲线

2）在垂足点N_i上，用方向架或经纬仪定出切线的垂直方向，沿垂直方向量出y_i，即得到待测定点P_i。

3）曲线上各点测设完毕后，应量取相邻各桩之间的距离，并与相应的桩号之差作比较，若差值均在限差之内，则曲线测设合格；否则应查明原因，予以纠正。(www.xing528.com)

（2）偏角法。偏角法是以曲线起点（ZY）或终点（YZ）至曲线上待测设点P_i的弦线与切线之间的弦切角Δ_i和弦长c_i来确定P_i点的位置。

如图7-16所示，依据几何原理，偏角Δ_i等于相应弧长所对的圆心角φ_i的一半，即Δ_i=φ_i/2。

则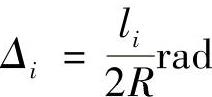

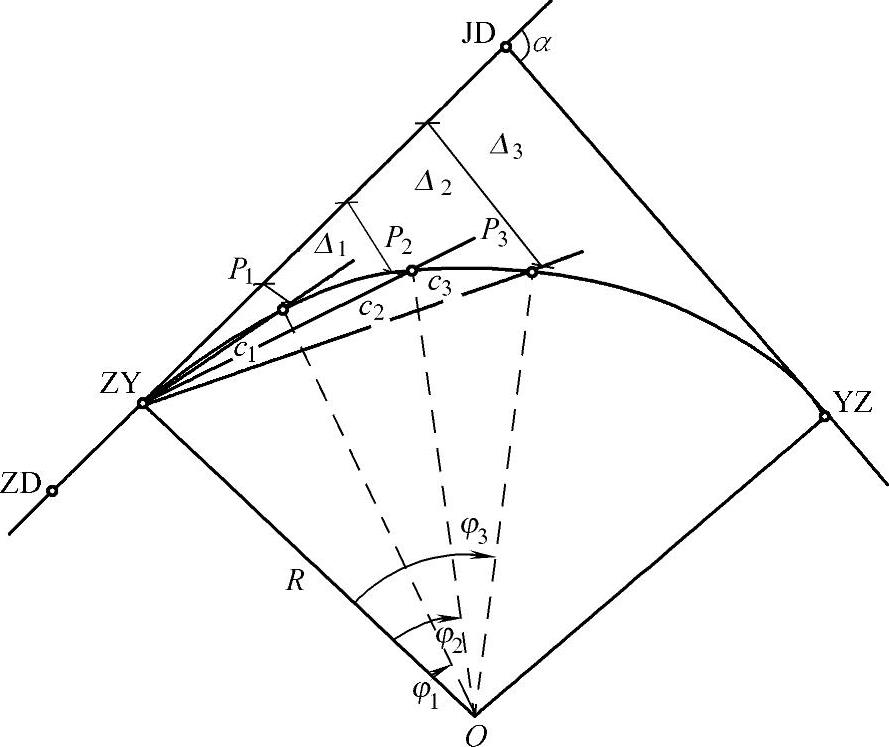
图7-16 偏角法详细测设圆曲线

弦长c可按下式计算

（3）极坐标法。用极坐标法测设曲线的测设数据主要是计算圆曲线主点和细部点的坐标，然后根据测站点和主点或细部点之间的坐标，反算出测站点至待测点的直线方位角和两点间的平距，依据计算出的方位角和平距进行测设，其操作步骤如下：

1）圆曲线主点坐标计算。如图7-16所示，若已知ZD和JD的坐标，则可按公式计算出第一条切线（图中的ZY—JD方向线）的方位角；再由路线的转角（或右角）推算出第二条切线（图中的JD—YZ方向线）和分角线的方位角。

2）圆曲线细部点坐标计算。由已知计算出的第一条切线的方位角α₁和待测设桩点的偏角Δ_i，计算出曲线起点（ZY）至各待测设桩点P_i方向线的方位角，再由ZY点到各桩点的长弦长，计算出各待测设桩点的坐标。