分层地基地下工程开挖对桩筏基础影响的验证

采用本书方法计算标准化后的Block 37基坑墙后土体位移，如图5-7和图5-8所示，分别为围护墙水平位移和墙后地表沉降的三维分布图。图5-9所示为在距离围护墙0 m、3 m、6 m、9 m和15 m处本书简化方法计算所得位移和有限元计算所得位移的比较。从图上可见，本书方法计算所得位移分布与有限元计算所得位移分布基本相似，且最大值基本一致。综上，本书计算方法是合理可行的。

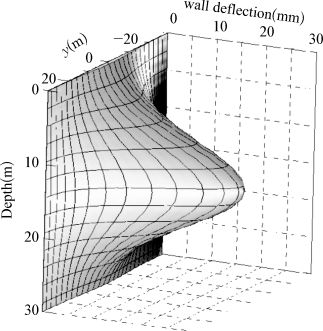
图5-7　围护墙位移图

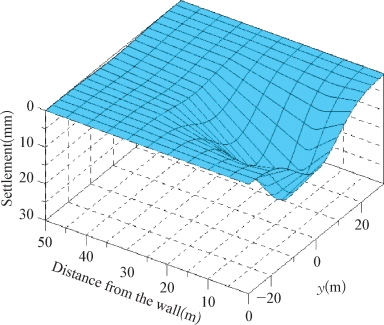
图5-8　墙后地表沉降

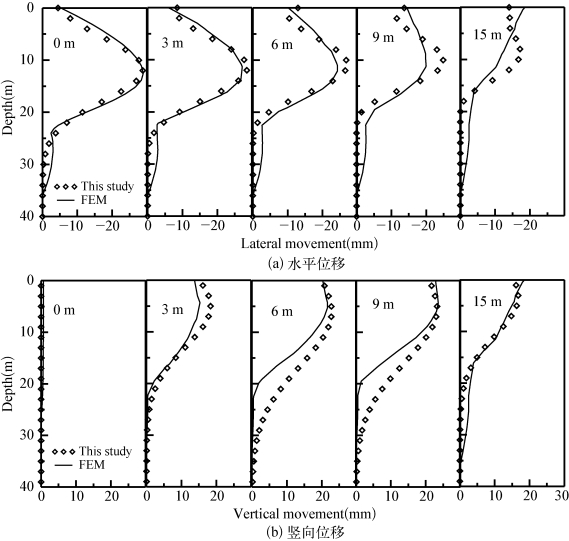
图5-9　围护墙后竖向截面位移对比

　　同时，本书也对芝加哥地区一实际基坑工程进行了分析。该实际工程为HRD-4基坑，位于芝加哥市区，基坑开挖深度为12 m，详细情况可见Finno和Harahap(1991)。图5-10所示为本书计算结果与实测结果的对比，从图上可见，在距离围护墙4 m的位置，本书计算结果要远小于实测结果，这是因为本书计算方法认为土体是个连续体，土体位移是连续的，而Finno和Harahap(1991)指出，在距离围护墙5～6 m处，土体顶部有一道较大的裂隙，因而使围护墙后距地表较浅的位置土体水平位移较大，在埋深较大位置，本书方法预测结果与实测结果符合得较好。由以上分析可知，本书方法只能计算土体连续的情况，而对于坑外土体开裂的情况，计算结果并不理想。(www.xing528.com)

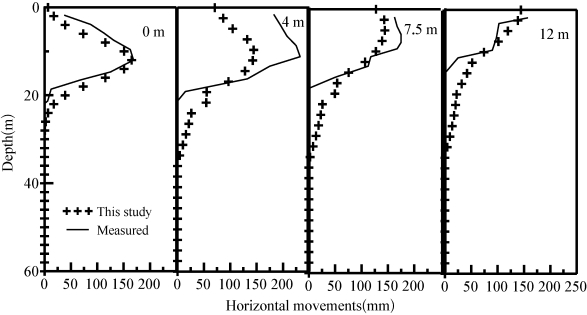
图5-10　HRD-4基坑计算结果

基于Block 37和HRD-4基坑，将本书方法计算结果和FEM计算结果以及实测结果进行了对比，可以看出本书方法是合理可行的，但是该方法也具有一定的限制：

(1)需要借助其他方法计算基坑开挖引起的最大围护墙水平位移；

(2)仅限于软土地区支撑架设较早，围护墙呈鱼腹式变形的情况，而不适用于悬臂梁式变形情况；

(3)适用于周边土体连续的情况，对基坑开挖引起周围土体开裂的情况也不适用。