基坑开挖对邻近桩筏基础的影响分析

上一节介绍了围护墙变形分布和墙后土体沉降变形分布的经验方法，但是，地表以下土体的位移情况不详，无法根据以上经验方法得到。上一章基于HSS模型采用反分析法，较为准确地计算了基坑开挖引起的围护墙变形和墙后土体沉降，本节拟采用有限元分析结果对墙后土体变形分布规律进行总结，拟合出墙后地表以下土体变形的计算公式。首先，由于Block 37基坑缺省首道支撑，其围护墙变形形态不符合式(5-1)所示情况，为了将基坑标准化，使其围护墙变形规律与式(5-1)所示相似，本书在第4章优化后参数的基础上对Block 37基坑架设首道支撑，计算基坑开挖引起的土体变形。

图5-2所示为有限元计算所得墙后土体水平向和竖向分布情况。从图5-2(a)可见，围护墙最大位移出现的位置稍高于基坑开挖面位置，所以在采用简化方法计算该项目时采用的H max不等于H，而采用实际计算所得最大位移位置。距离围护墙0 m(围护墙)和1 m土体水平位移基本一致，随后，随着与围护墙距离的增加，水平位移开始衰减。在离围护墙1倍开挖深度的距离范围内，每个截面的水平位移最大值出现在靠近基坑开挖面深度的位置，离围护墙大于1倍开挖深度的距离外，土体水平位移最大值出现在地表。且可以看到本书采用的围护墙的变形公式计算结果与有限元计算结果基本一致，而在围护墙埋深底部面以下，计算结果较有限元结果小。同样可以从图5-2(b)看到，距地表0 m和1 m的水平面土体竖向位移基本一致，随着深度的增加，土体竖向位移减小，在开挖面以上，同一个水平面土体最大竖向位移值出现在靠近距围护墙0.5倍开挖深度的位置，而在开挖面以下，同一个水平面上土体最大竖向位移出现在靠围护墙的位置。竖向经验方法计算所得地表土体竖向位移基本与有限元计算结果一致。

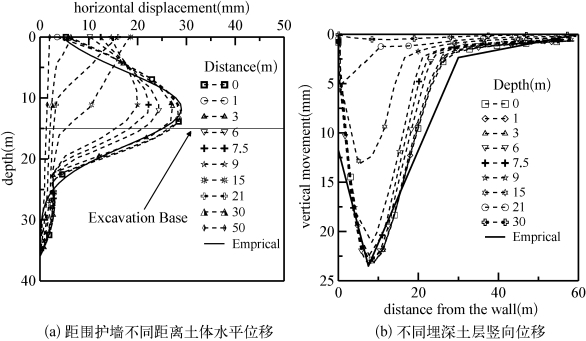
图5-2　墙后土体位移

因为围护墙水平位移和墙后地表沉降可以通过经验公式确定，因此，研究土体水平位移沿水平方向的衰减规律和土体竖向变形沿深度方向的衰减规律是确定墙后土体位移场的关键。图5-3所示为水平位移沿水平方向的衰减和竖向位移沿深度方向的衰减规律，从图上可见，在距围护墙1 m范围以内，水平位移基本保持一致，且在0.5倍开挖深度以内，水平位移随着离围护墙距离的增加先增加后减小，因为在这一深度范围内，随着与围护墙的距离的增加，土体应变先增加后减小(图5-4)，而土体模量在小应变范围内，随着应变的增加而减小(图4-10)，导致位移先增加后减小，从图5-4可见，应变峰值和位移峰值与围护墙的距离基本一致。而深度超过0.5倍距离之后，水平位移随着距离的增加而减小。同样在距离地表1 m范围以内，竖向位移基本保持一致，而深度超过1 m之后，在距离围护墙0.5倍开挖深度范围内，竖向位移先增加后减小，在0.5倍开挖深度范围以外，土体竖向位移随深度增加而减小。

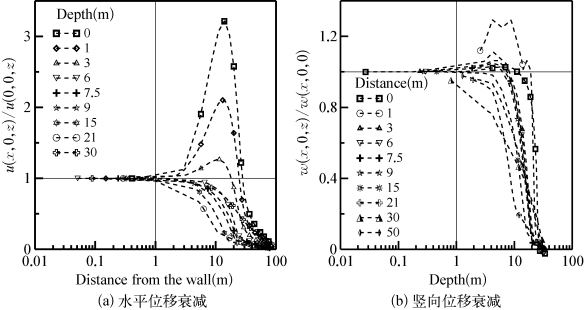
图5-3　墙后土体衰减规律

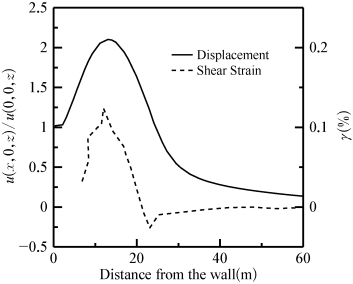
图5-4　埋深1 m处水平位移峰值和剪应变峰值

采用埋深对水平位移衰减曲线进行无量纲化和采用与围护墙距离对竖向位移衰减曲线进行无量纲化，如图5-5所示。图中由于竖向位移衰减在贴近围护墙的位置受接触面单元的影响，无法取得合理的衰减曲线，因此，在拟合过程中，舍去距围护墙0 m和1 m处竖向位移衰减曲线。从图上可见，可采用如下方程对竖向和水平向衰减的每条曲线进行拟合：

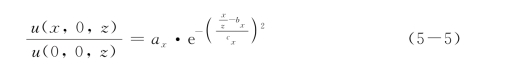
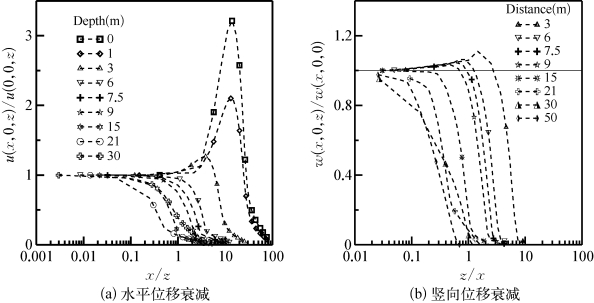
图5-5　归一化后土体位移衰减规律

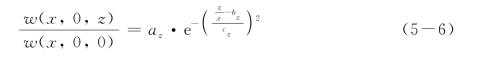
式中，u(0，0，z)为围护墙水平位移，w(x，0，0)为墙后地表沉降，a x、bx、c x、az、bz和c z为需要拟合的参数。

采用式(5-5)和式(5-6)对各条曲线拟合后的系数如表5-1所列。从表上可见，各系数均随着深度或者距离的增加而减小，说明可建立各系数与深度或者距离的关系式。同时，为了考虑开挖深度的影响，本书采用与开挖至15 m时相同的处理方法，对Block 37项目分别开挖至7 m和12 m时的位移衰减曲线也进行拟合，最后将所有系数分别与距离和开挖深度比值(x/H)或者深度与开挖深度比值(z/H)建立关系，如图5-6所示。(www.xing528.com)

表5-1　各曲线拟合系数

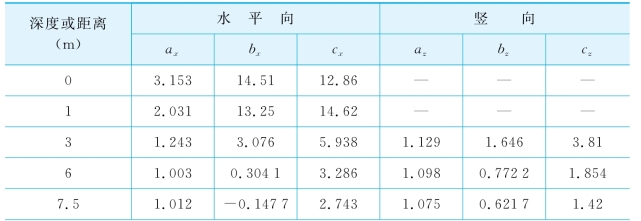
续　表

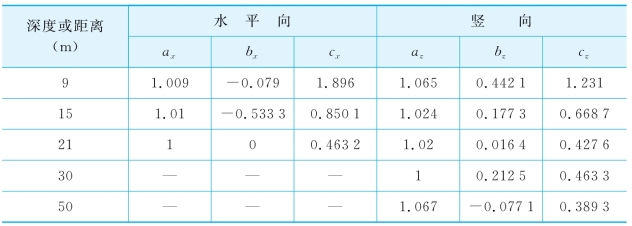
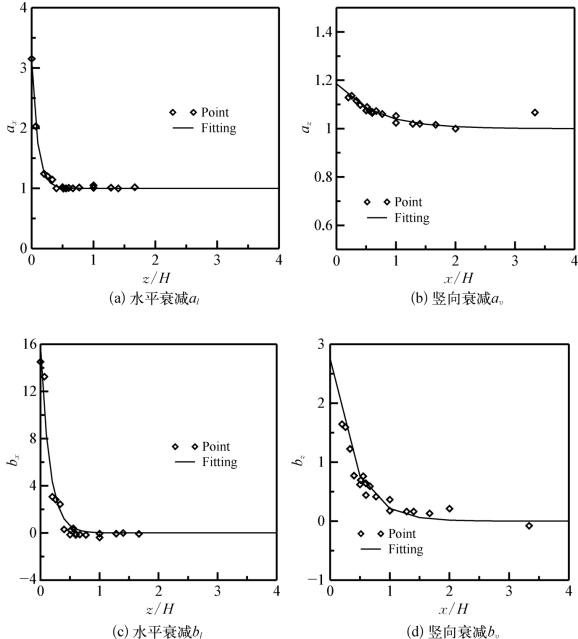
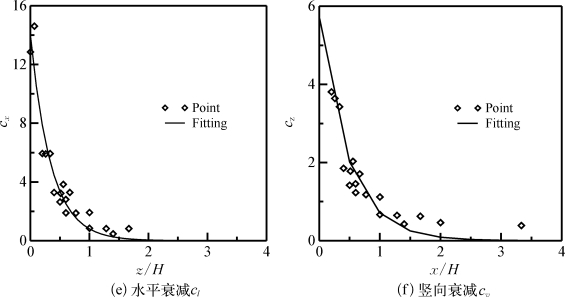
图5-6　各系数分布曲线

　　从图5-6可见，各系数随着z/H或者x/H的增大而减小，并且可以用以下式子来拟合：

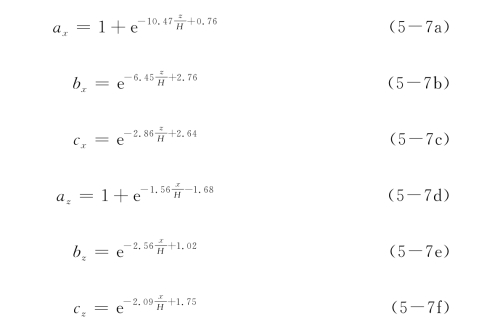
结合式(5-1)、式(5-4)、式(5-5)和式(5-7)，可以得到在最大水平位移已知时墙后任意点土体水平位移计算式：

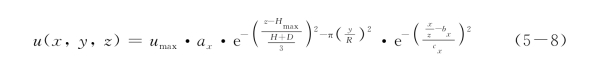
结合式(5-2)、式(5-3)、式(5-6)和式(5-7)，可以得到墙后任意点土体竖向位移计算式：

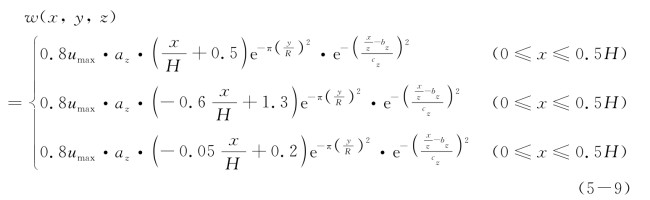
式中，u l，max为围护墙最大水平位移值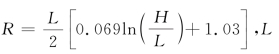，为基坑沿围护墙方法开挖长度，H为基坑开挖深度，a x、bx、c x、a z、bz和c z可见式(5-7)。