基坑实测揭示地下工程对桩筏基础影响分析

如前所述，实测数据中，开挖至第一道支撑时记录的位移可以较为准确地反映基坑开挖引起的土体位移，且因为预开挖的尺寸不详，所以预开挖的位移可能不能准确反映开挖引起的土体位移，但是，从预开挖结束到开挖至第一道支撑之间的位移增量由于受到的其他影响较小，可认为是开挖卸载引起的位移，因此，本书采用开挖至第一道支撑时与预开挖结束时之间的位移增量作为反分析的实测值来进行参数分析。三轴试验反分析中，本书分析了ψ、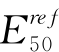和γ0.7，而在三轴试验分析中可知，芝加哥黏土为正常固结土和轻微超固结土，ψ值为接近0的数，因此，在基坑分析中，认为ψ为0，所以基坑开挖仅对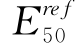和γ0.7两个参数进行优化分析。

图4-28所示为优化后计算结果和实测结果的对比。图中所示位移为该阶段位移与预开挖产生的位移的差值，即位移增量。从图上可见，在第一阶段，无论是用HSS模型还是用HS模型，侧向位移均与实测值一致，这说明反分析的结果是正确的。利用反分析所得参数计算预开挖以及开挖至坑底时的位移。从图上可见，HSS模型能够较好地计算预开挖引起的位移，与实测值基本一致，而HS模型计算值要明显小于实测值。同样，在开挖至坑底后，HS模型的计算值也要小于实测值，这是因为在第一步开挖的时候位移还较小，土体还处于小应变状态，因此，基于HS模型用第一步开挖的位移增量来进行反分析时高估了土体的刚度，因此计算得到的其他阶段的位移均要比实测位移值小。而用HSS模型计算最终位移时，在开挖面以下，计算位移与实测位移一致，而在开挖面以上，埋深越小的位置，计算值与实测值差异越大，最大差异达到10 mm左右。这是因为混凝土板的收缩徐变使开挖面以上围护墙位移大于开挖卸载引起的位移。

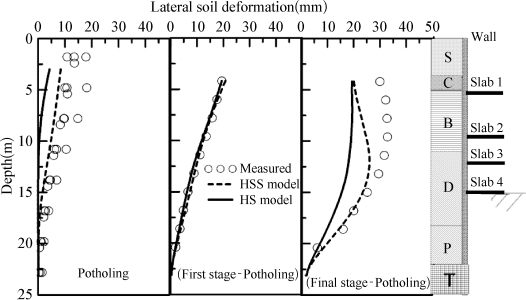
图4-28　优化后计算墙体位移与实测结果对比

图4-29所示为采用优化后参数计算所得墙后土体沉降与实测值对比。从图上可见，在第一阶段，HS模型计算所得沉降曲线与HSS模型计算得到的沉降曲线相近，与实测结果较为接近，最大沉降值与实测值一致；而在最终阶段，HS模型计算所得沉降曲线要比HSS模型计算得到的沉降曲线浅且平，但是，无论是HSS模型还是HS模型，计算所得结果都要比实测结果小很多，这是因为混凝土收缩徐变造成了额外的围护墙水平位移，同时也引起的墙后土体的额外沉降。

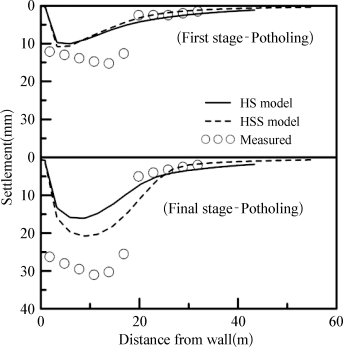
图4-29　优化后计算墙后土体沉降与实测结果对比

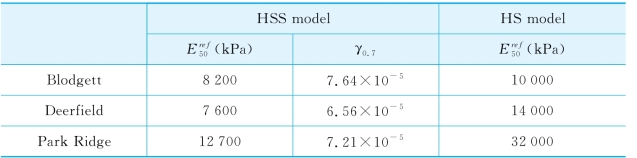
表4-11所列为基坑反分析得到的参数。从表上可见，在基坑分析中，基于HSS模型分析得到的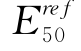值与三轴压缩试验分析中得到的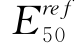较为接近，而基于HS模型得到的要明显大于从三轴试验得到的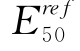。这是因为反分析采用的实测值是第一阶段的土体位移，该阶段土体还处于小应变阶段，土体刚度要明显高于大应变时的刚度，因此，HS模型高估了土体的刚度。从基坑分析得到的γ0.7与三轴拉伸试验中得到的γ0.7相近。通过HS模型参数与HSS模型参数的对比，可知γ0.7对土体刚度具有重要影响，因此，本书又对γ0.7对基坑开挖引起周边土体变形的计算结果的影响进行了分析。如表4-12所列，分析了HSS模型中待优化参数的CSS值，可见γ0.7对计算结果的影响与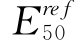同样重要。也可以从图4-30上看出，γ0.7值越大，围护墙变形越小，因此，在基坑开挖分析中考虑土体的小应变对准确预测结果来说是尤为重要的因素。(www.xing528.com)

表4-11　基坑反分析结果

　　Note：pref=100 kPa。

表4-12　基坑分析中待分析参数的CSS

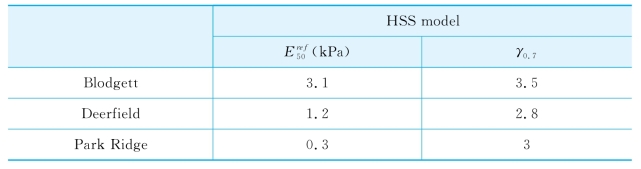
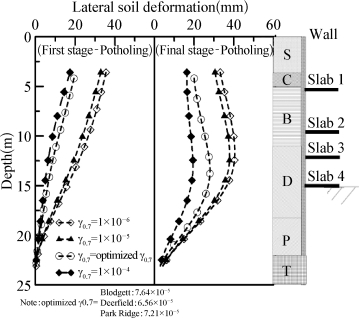
图4-30　γ0.7对计算结果的影响