三轴试验确定土体参数及其对邻近桩基影响分析

基于以上试验结果，采用本书反分析方法确定室内三轴试验所得参数。

1.反分析参数的选取

反分析具有结果非唯一性的缺点，同时，进行反分析的参数越多，得到相同结果的组合数的可能性越多，这种缺陷表现得越明显。因此，要克服这种缺陷，需要减少同时进行分析的反分析参数。反分析参数的选取主要根据输入参数对结果的影响的重要程度，Calvello(2002)指出，百分比敏感度(CSS)可以有效地表示输入参数对结果的影响的重要程度，并对HS模型的各参数的百分比敏感度进行了分析，指出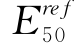和m对结果有较为重要的影响，并且通过相关系数的分析指出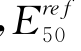，和m具有较大相关性，不能同时进行分析，且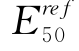相对m更能体现土体的刚度。因此，Calvello(2002)指出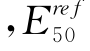对土体刚度分析具有重要的影响作用，应作为反分析参数。在HSS模型中，由于对剪胀角进行了修正且增加了两个控制小应变的参数，所以本书将对这三个参数进行探讨。

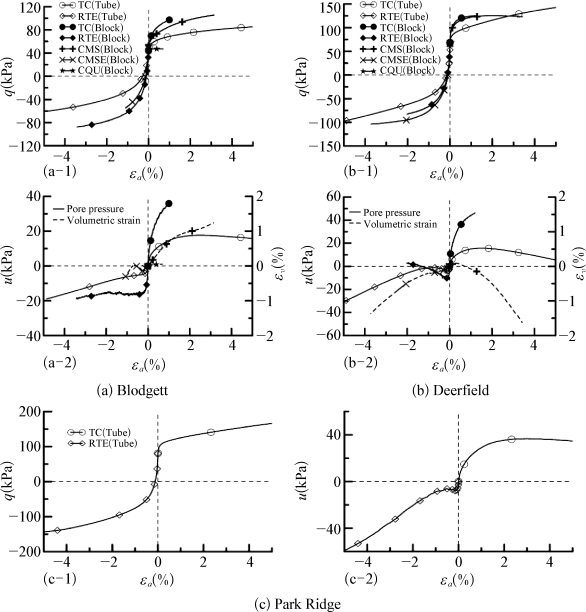
图4-19　三轴试验结果

如图4-20所示，在Block土样固结至原位土压力并经过36小时的排水蠕变之后测得的剪切波速与现场动态CPT测得的剪切波速基本一致。剪切模量可按照式(4-28)由剪切波速计算得到。可见室内试验和现场试验所得初始剪切模量是较为一致的，因此认为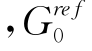是定义较为合理，可以从试验确定比较合理的取值的参数，无需进行反分析。因此，本书选定剪胀角ψ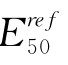，和γ0.7作为反分析对象参数。

表4-6列出了三个待优化参数的CSS值，可见三个参数的CSS值均在相当的量级，因此，同时分析该三个参数是合理的选择。反分析中，初始参数采用Calvello(2002)根据Chicago State基坑反分析所得最终值，其中，γ0.7采用表4-3所列方法初步估计。

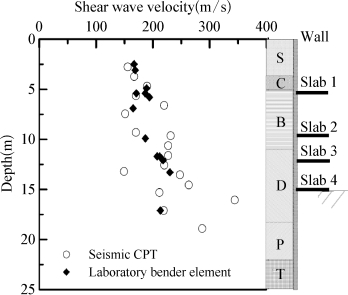
图4-20　剪切波速

表4-6　三轴试验中HSS模型待反分析参数的CSS

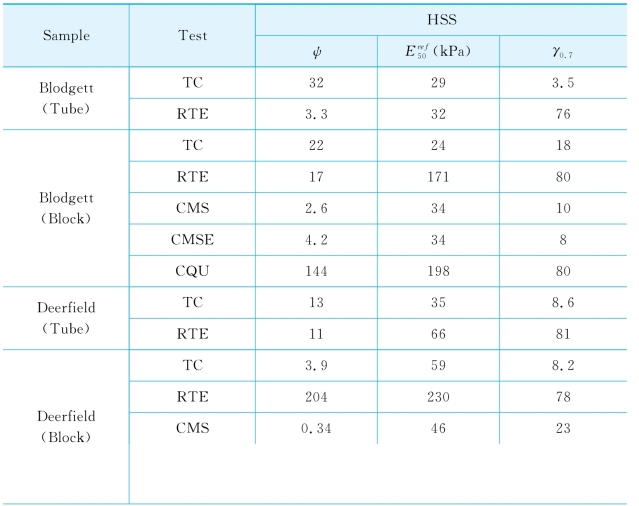
续　表

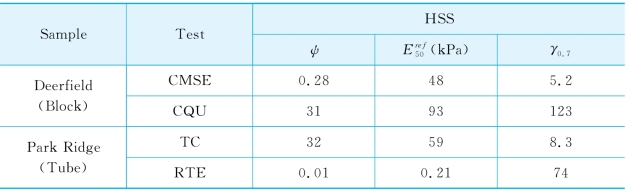
　　2.测量值的选取

选定待分析参数后，要取得合理的结果，需要选取合适的测量值作为参照结果。对于不排水三轴试验，本书采用主应力增量以及孔压与轴向应变的关系曲线作为反分析所需实测结果；对于排水三轴试验，本书采用主应力增量以及体积应变与轴向应变的关系曲线作为反分析所需实测结果。实测点的分布与测试结果有关，对于HSS模型，轴向应变从0.001%～0.1%之间每隔0.005%分布一个点，轴向应变从0.1%～1%之间每隔0.05%分布一个点，轴向应变从1%到破坏时应变值之间，每隔0.5%分布一个点，这样，实测点的分布能够合理地代表土体小应变和大应变特性。对于HS模型，由于不存在小应变部分，仅取轴向应变大于0.5%的点作为实测值，其分布于HSS模型采用的实测值点分布一致。由于对不同试验选用了不同数量的实测值，因此，用实测点数目归一化目标方程值，之后讨论的目标方程值为归一化后的目标方程值(F′(b))。(www.xing528.com)

3.反分析结果

图4-21所示是在普通坐标下Blodgett土样TC、RTE、CMS和CMSE的试验结果与HSS模型最佳计算结果的对比。其他土样的结果以及采用HS模型的结果可见附录1。所谓最佳计算结果，即是采用反分析所得参数计算所得土体的应力-应变曲线。同时，图上也标注了对应的归一化目标方程值，归一化目标方程值越小，说明计算结果与试验结果拟合得越好。从图上可见，虽然采用合理的参数HSS模型能够准确预测土体的应力-应变曲线，但是，HSS无法准确预测RTE试验中土体的孔压响应。从附录可见其他土样试验和HS模型也具有相同结果。

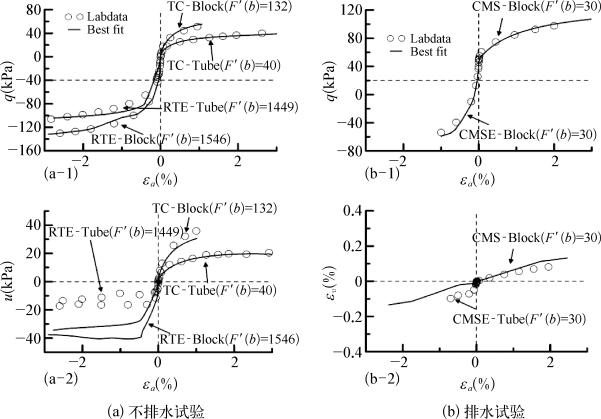
图4-21　Blodgett土三轴试验最优化结果与实测值对比

为研究土体的小应变特性，图4-22所示为在对数坐标下归一化后的土体剪切模量与剪切应变实测与计算值的对比曲线。图中剪切应变定义为2(εaεr)/3，其中，εa为轴向应变，εr为径向应变。正切剪切模量通过除以由弯曲元确定初始剪切模量来归一化。从图上可见，在小应变时，从拉伸试验所得的剪切模量要比从压缩试验得到的剪切模量大。从拉伸实验得到的初始剪切模量相比从压缩试验得到的初始剪切模量更接近于从弯曲元得到的初始剪切模量。Kung(2009)指出，这种现象有可能是因为在压缩试验中由于测试精度无法测量土体弹性响应所致。而且可以看到，采用Block土样的拉伸和压缩试验的初始G sec/G 0值之差要比采用Tube土样的拉伸和压缩试验的初始G sec/G 0的差小。这可以从某个方面说明Block土样要比Tube土样质量稍好，因为从理论上来说，土体的初始刚度应该一致，Block土样在各试验中初始刚度的一致性要比Tube土样好。也可以看到，相比TC(Tube)、TC(Block)所测得的初始剪切模量与现场实测所得到的初始剪切模量更为接近。从图上可见，从拉伸试验得到的芝加哥黏土的γ0.7值大约为0.01%，而从压缩试验得到的γ0.7值要小于0.001%且无法由试验内部测试系统测得。总的来看，采用反分析所得参数，HSS模型能够合理模拟土体的应力-应变特性，而且要比HS模型更为合理。

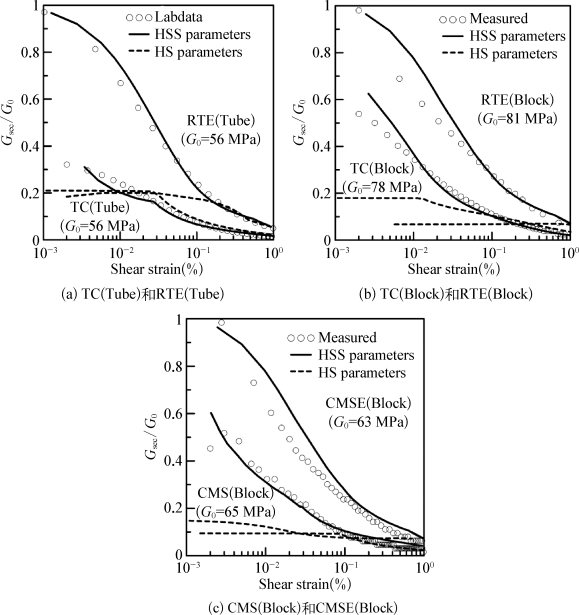
图4-22　Blodgett土样三轴试验计算与实测土体刚度曲线对比

表4-7所列为三轴试验反分析结果。从图4-22和表4-7可以看出，当归一化目标方程值F′(b)小于150时，说明反分析的结果是一个合理的结果。从表可见，即使采用反分析后的参数，HSS模型也无法准确模拟RTE试验中的孔压响应和CQU的应力-应变曲线。从表上也可见，剪胀角ψ一般小于1，这与芝加哥黏土是正常固结或者低微超固结土的性质一致，其中，Blodgett(Tube)和Park Ridge的RTE试验以及Blodgett(Block)土样CMSE试验的ψ值明显大于1，这可能是因为HSS模型无法模拟RTE试验的孔压以及在CMSE试验中，仅轴向应变小于1%的点被用来作为实测数据。从表中可见，由压缩试验所得的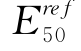值与Calvello(2002)基于排水TC试验分析所得结果一致，而由拉伸试验所得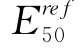值仅为压缩试验所得值的1/3～2/3。图4-23解释了这种差异的由来，图中分别为采用Blodgett土样的TC(Block)试验所得参数计算所得在K 0和等相固结条件下，TC和RTE试验的应力应变曲线。HS模型和HSS模型中是根据等相固结条件下排水TC试验定义的。从图中可见，采用相同参数模拟等相固结后的TC和RTE试验，因为两者都是“加载”试验，表现出了相同的刚度。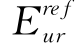而用相同的参数模拟K 0固结状态下的TC和RTE试验时，因为TC是“加载”试验，而RTE则为“卸载”试验被用来计算TC试验的应力-应变特性，而被用来计算RTE试验的应力-应变曲线。而在PLAXIS中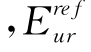被定义为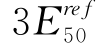，所以，从RTE得到的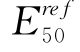实际上应该为从TC得到的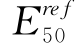的1/3。而从表5-7可以看到，从拉伸试验得到的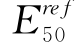基本上为从压缩试验得到的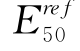1/3～1/2，规律是正确的。这也说明，在反分析过程中，不应该使用拉伸试验来分析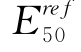的值。同时，从表4-7也可以看出，基于相同的实验数据，HSS模型和HS模型所得的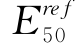是不一样的，因此，在使用HSS模型时，不能随意使用HS模型得到的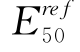值。

表4-7　三轴试验反分析结果

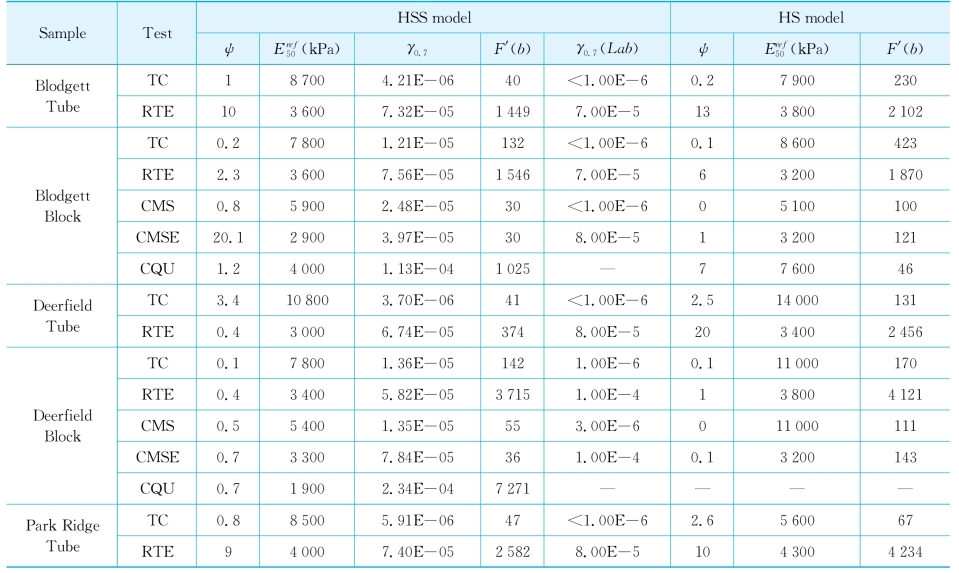
注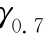：（Lab）为实测结果。

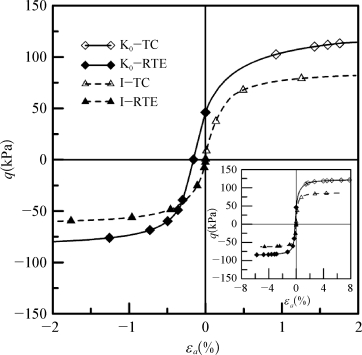
图4-23　TC与RTE的应力-应变曲线

从表4-7也可以看到，对于拉伸试验，反分析所得的γ0.7与按照定义从图4-22得到的γ0.7的值相近，而对于压缩试验，反分析所得值比0.000 1%小，且按照定义无法从图4-22得到γ0.7，因为试验设备无法测得应变小于0.001%的数据。这是因为在分析过程中采用了弯曲元测得的G 0代替小应变测试系统所测得最大G sec作为初始刚度。总的来说，无论是HS模型还是HSS模型，都无法用同一组参数来计算不同应力路径下土体的应力-应变特性，这与Finno和Cho(2011)得出的结论是一致的，土体的应力-应变特性与土体的应力历史和应力路径具有重要的联系。