在HS模型中,土体刚度在卸载和再加载时认为是线弹性的,在土体中,当应变非常小的时候,这可能符合实际情况,然而,随着应变的增加,土体就开始显现出非线性。如图4-9所示,土体刚度与应变的log值画出的曲线呈S型分布。同时,图中也标出了各种实际岩土工程中土体的大概剪应变范围以及实验室所能测得的最小剪应变值。
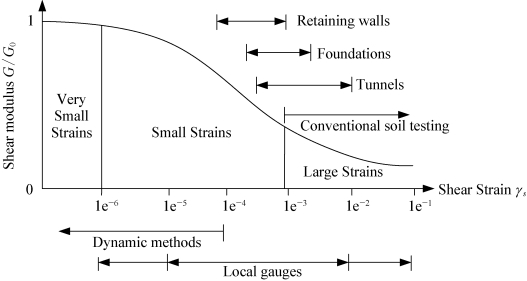
图4-9 土体小应变刚度特征曲线
在岩土工程问题中,不仅仅要考虑岩土结构施工完毕时的土体刚度,小应变状态下,土体的刚度也需要考虑在内。HSS模型能够全面考虑岩土工程中各种应变分布条件下土体的刚度。PLAXIS中,HSS模型和HS模型具有基本相同的参数,但是,HSS模型多了两个参数来控制小应变状态下土体的刚度:
a.初始剪切模量G 0。
b.当剪切模量Gs减小到0.722G 0时,剪切应变γ0.7。
1.描述小应变刚度的双曲线法则
在土动力学中,很久以前就开始发现土体的小应变特性,而在静力学中,虽然也注意到了小应变特性,但是一直没有得到应用。表面上,静力和动力状态下土体的刚度不同主要是因为荷载的性质不同而不是因为动荷载下土体的应变较小,实际上,因为内力和应变比对土体的初始刚度的影响很小,因此,土体的动模量和小应变模量是同一个模量。
在动力分析中,最普遍的模型是Hardin-Drnevich模型。实验数据表明,小应变状态下,应力应变关系可以用一个简单的双曲线模型表示。Hardin和Drnevich(1972)采用如下公式来描述这种双曲线关系:

其中,临界应变γr=τmax/G 0,τmax为土体破坏时的剪力值。
更直接、误差更小的做法是采用较小的临界应变值,Santos和Correia(2001)建议采用Gs=0.722G 0的剪应变值为临界应变值,即

其中a=0.385。
2.Hardin-Drnevich准则在HSS模型中的应用
在HSS模型中,应力应变关系由割线剪切模量表示如下:
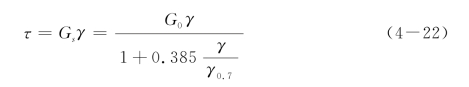
在HS模型中,刚度的衰减是通过应变硬化来模拟,所以,HSS模型中,小应变状态下的刚度衰减规律有一个上限值,且这个值可以通过实验确定,这个界限可以用下式表示:
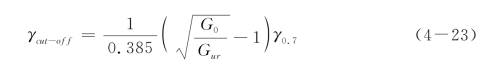
其中,Gur为卸载/重加载剪切模量。
即当剪应变小于γcut-off时,土体刚度衰减由小应变的Hardin-Drnevich关系式表示,当剪应变大于γcut-off值时,由应变硬化准则来控制刚度的衰减。
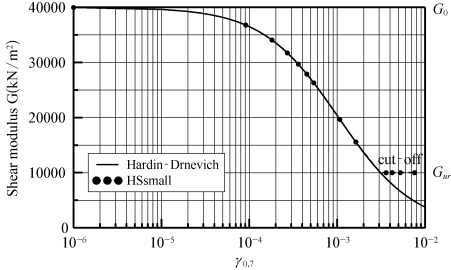
图4-10 HSS模型刚度典型衰减曲线
3.HSS参数模型(https://www.xing528.com)
相对于HS模型,HSS模型增加了两个参数,如表4-3所列。
表4-3 HSS模型相对于HS模型增加的参数

主荷载作用下的剪切模量G 0可由下式计算:

当缺乏足够的实验数据来确定γ0.7的时候,可以用下式来估计γ0.7值:

其中,K 0为静止土压力系数,σ′1是竖向有效应力。
4.HS模型和HSS模型的其他不同
相对于HS模型,HSS模型除了考虑小应变外,也对驱动剪胀角进行了修正。HS模型和HSS模型的剪切硬化法则都可以表示为如下线性关系:
![]()
但是在压缩时,HS模型和HSS模型对发挥的剪胀角的定义不同。
在HS模型中假设:
当sinψm<3/4sinφ时,ψm=0
当sinψm≥3/4sinφ且ψ>0时,![]()
当sinψm≥3/4sinφ且ψ≤0时,ψm=ψ
如果ψ=0,则ψm=0
其中φcv是临界状态摩擦角,φm是发挥摩擦角:
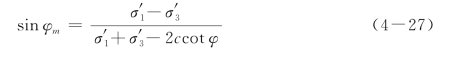
当发挥内摩擦角较小时或者ψm为负值时,HS模型中均假设ψm为0。但是,设置ψm的下限值有可能会造成计算塑性体积应变过小。因此,在HSS模型中,采用Li和Dafalias(2000)提出的方法,经过Benz(2007)简化后,可用如下公式来计算发挥剪胀角:
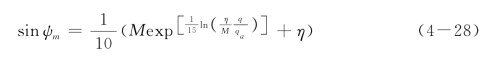
其中,M是破坏时的应力比,η=q/p是实际的应力比。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




