【摘要】:在优化过程中,有些输入参数的值可能有某些限制,程序使用者不能随意设置该参数的上下限。在实际岩土工程问题中,很多参数都有其自然的限制。比如可以用如下双曲线方程表示输入参数x:其中,x是待估计参数,y 1是x的下限,y 2是x的上限,Tan是曲线在y-e x空间中的初始正切值。当自然条件下模型输入参数在某个值附近时,Tan可以表示如下:图4-2输入参数的双曲线转换模型
在优化过程中,有些输入参数的值可能有某些限制,程序使用者不能随意设置该参数的上下限。Hill等(1998)指出,这有可能是模型的不精确性的另一种表现。事实上,造成反分析结果不符合实际的原因主要可能有两个:(1)模型中还有基本的错误;(2)测量值包含的信息量不足以合理估计输入参数。对于第一种情况,就需要使用者仔细排查模型中可能存在的问题。而对于第二种情况,可以对需优化的参数进行拆分,或者使用参数值的初始信息。使用参数值的初始信息就是在回归过程中使用参数的直接测试结果,将其作为实测值中的某个实测点,使优化后的参数接近某个特定的值。
在实际岩土工程问题中,很多参数都有其自然的限制。很多模型中的很多参数值必须是正值(比如杨氏模量、黏聚力),有些具有上、下限(比如泊松比、内摩擦角)。因此,在程序使用过程中,使用者需要指定某些被优化输入参数的上、下限,或者可以使用有界方程来代替实际的输入参数。比如可以用如下双曲线方程表示输入参数x:
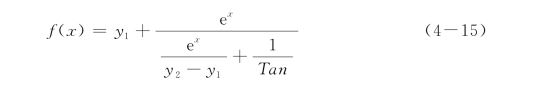
其中,x是待估计参数,y 1是x的下限,y 2是x的上限,Tan是曲线在y-e x空间中的初始正切值。
对x的限制如图4-2所示。当自然条件下模型输入参数在某个值附近时,Tan可以表示如下:(https://www.xing528.com)

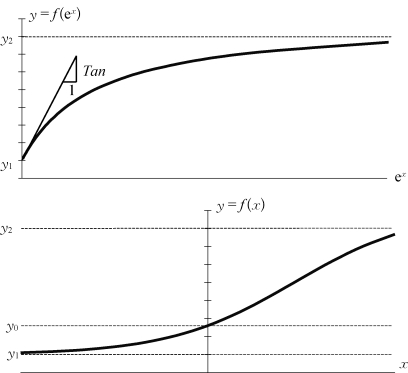
图4-2 输入参数的双曲线转换模型
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




