地下开挖对桩筏基影响分析—方法建立

1.隧道开挖对单桩的影响

与第2章建立主动单桩差分方程相同，假定单桩长为L，桩的直径d，桩端直径为d b，桩顶受轴力Q的作用，把桩分成n个单元，δ=L/n。以桩侧摩阻力为未知量，分别取桩周土和单桩建立节点的位移方程，根据桩土之间的位移相容条件，建立平衡方程，解得桩身各节点处的摩阻力，然后可求出各节点处的位移。

A.桩身平衡方程

与第2章第2.2节相同，建立桩身平衡方程：

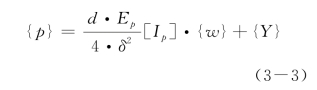
B.土体平衡方程

　图3-7　土体竖向位移示意图

如图3-7所示，假设隧道开挖引起的桩轴线处土体自由场竖向位移向量为{Sz}，且桩身位移与桩侧土位移协调，桩土界面的实际位移为{w p}，即桩的存在将减小土体位移，由桩周力引起的土体位移为{Sz}-{w p}，则可得到土体的位移方程：

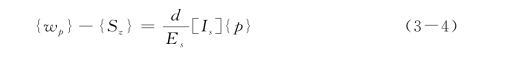
式中，{Sz}={Sz，1　Sz，2　Sz，3　…　Sz，n　Sz，b}T，其他参数同第2章。

C.整体平衡方程

最后，将式(3-3)和式(3-4)联立，可以得到单桩的整体差分方程：

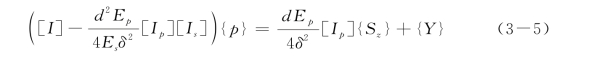
式中，[I]为单位阵。

通过式(3-5)求出桩周阻力{p}之后，可以求出桩身位移{w p}及桩身的附加轴力。

2.层状地基中隧道开挖对群桩基础的影响

隧道开挖对群桩的分析主要分为两部分：①群桩中基桩的附加位移和附加内力分析；②被动群桩中桩和桩、桩和土之间的相互影响分析。上一部分已经详细介绍了隧道开挖对基桩的影响的分析方法的建立，这里着重于介绍桩桩相互作用的计算。桩桩相互作用分为主动桩相互作用和被动桩相互作用，主动桩的相互作用包括桩桩相互作用系数和加筋效应系数，在考虑该两种效应的同时，需要考虑桩基对被动位移的遮拦效应。第2章已经详细介绍了桩桩相互作用和加筋效应，以下将针对遮拦效应展开详细讨论。

Loganathan(2001)等指出，被动群桩具有明显的遮拦效应，当考虑遮拦效应时，群桩中基桩的位移和内力均比单桩时明显减小。所谓“遮拦效应”，是指桩基对周边土体发生运动所作的抵抗，在此处表现为隧道开挖引起的土体位移因为桩基的存在而减小，土体被动位移的减小也必将导致桩基位移减小，所以也表现为当前桩的存在会导致其他桩被动位移减小。李早等(2007)基于剪切位移法对隧道开挖条件下被动群桩的遮拦效应进行了分析。但是剪切位移法在分析群桩时仅考虑桩土在平面内的相互作用，忽略了同一根桩上不同点间的相互作用，且未考虑桩基变形引起的土体变形。为了与主动桩沉降引起土体变形相区别，本书将被动桩分析中桩基变形引起的土体变形作用归纳为桩基变形导致遮拦效应的减弱，即表现为土体同一点的被动位移在桩基变形时比在桩基不变形时的被动位移要大。这是因为桩基变形时，桩侧阻力将比不变形时小，而桩侧阻力正是遮拦位移大小的决定性因素。因此，遮拦效应的大小依赖于桩基最终变形状态。所以，本书采用整体求解方式，即遮拦位移方程与桩基整体方程同时联立求解，此时得到的桩基位移和侧摩阻力为最终状态的位移和侧摩阻力，而此时得到的遮拦效应也即为考虑了桩基变形对遮拦效应削减之后的最终遮拦效应。

本书基于层状体系弹性理论法，分析群桩的遮拦效应，如图3-8所示。由于桩1的存在在桩2位置处的土体遮拦位移为(www.xing528.com)

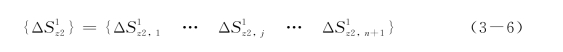
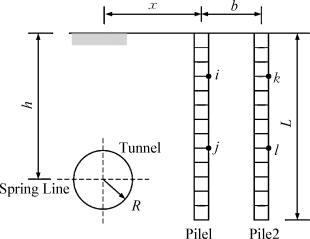
图3-8　群桩计算模型

式中，

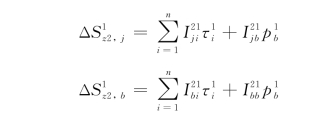
其中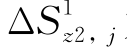，为由于桩1的存在在桩2第j段位置处的土体遮拦位移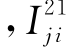为桩1第i段的单位桩侧阻力引起的桩2第j段位置处的土体遮拦位移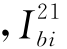为桩1第i段的单位桩侧阻力引起的桩2桩端位置处的土体遮拦位移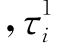为桩1第i段的桩侧阻力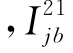为桩1桩端阻力引起的桩2第j段位置处的土体遮拦位移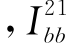为桩1桩端阻力引起的桩2桩端位置处的土体遮拦位移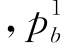为桩1桩端阻力，分层地基中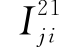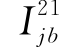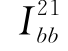，，，可以通过层状地基中轴对称问题基本解求解。

假设被动群桩桩数为m，则桩2处的土体遮拦位移为

所以，桩2处土体位移为{Sz}-{ΔSz2}，则桩2的整体差分方程为

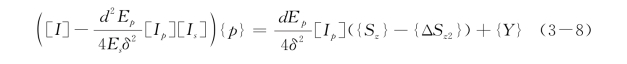
同理可以列出其他桩的整体方程，联立m个方程求解，则可以求得各桩的附加位移和内力。

3.层状地基中隧道开挖对桩筏基础的影响

隧道开挖对邻近桩筏基础的影响分析与隧道开挖对邻近群桩基础的影响分析的不同在于桩筏分析需要在群桩分析的基础上同时考虑筏板与土的相互作用以及筏板与桩的相互作用。因此需要引进两个约束条件：①筏板最终沉降等于不考虑筏板存在时桩土被动位移与筏板约束产生的桩土位移之和(筏板和桩、筏板和土界面处位移协调)；②桩土单元对筏板竖向作用力之和为0(假设筏板上没有外荷载)，这两个约束条件可表示为

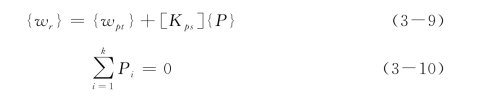
式中，{w r}为与筏板接触的桩土单元最终位移向量，{w r}={w r1　w r2　…　w ik}T；{w pt}为不考虑筏板存在时相应的桩土单元顶的被动位移，在计算土单元位移时，将土单元假设为虚拟桩，计算桩对土单元的作用系数、土对桩的作用系数，以及桩对土的“遮拦位移”，{w pt}={w pt 1　w pt 2　…　w pt k}T；[K ps]为与筏板接触的桩土单元的刚度矩阵；{P}为桩土单元与筏板的相互作用力，{P}={P 1　P 2　…　P k}T；k为平面内桩土单元总数。

其中，αii为桩桩相互作用系数；βi(m+j)为土对桩的作用系数；κ(m+j)i为桩对土的作用系数；η(m+j)(m+j)为土对土的作用系数。

Loganathan等(2001)计算结果表明在被动群桩分析中，土体沉降要大于桩顶沉降，因此，在不考虑上部荷载作用的情况下，被动刚性桩筏基础分析中，由于桩变形较小，土体将与筏板脱开，两者之间不存在相互作用。所以，在刚性筏板被动群桩分析过程中，仅需考虑桩与筏板的相互作用，而不用考虑土体与筏板的相互作用。当考虑上部荷载作用时，土体与筏板是否分开依赖于上部荷载大小和被动荷载的大小的比值，因此需考虑筏板与土接触以及不接触两种情况，取其不利情况进行设计。