地下工程开挖对邻近桩筏基础的影响分析！

如图2-8所示，在m层的地基中，单桩桩长为L，直径为d，桩顶作用竖向力Q、水平力P和弯矩M。以下将分别列出竖向和水平向单桩的计算方法。

1.竖向单桩计算方法

将桩分为n段，每段长为δ=L/n，以桩周侧摩阻力为未知量，分别建立桩身和土体平衡方程。

A.桩身平衡方程

单桩桩身的分析采用等间距的差分格式，建立桩身平衡方程。桩身的位移控制方程：

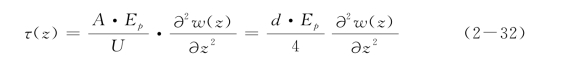
式中，w为桩身结点的竖向位移；E p为桩的弹性模量；A为桩身截面积；U为桩身周长；d为桩直径。

从桩顶起，对于第2个至第n个单元，可以写出

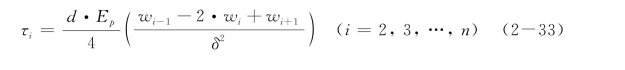
对于第一个单元，引入虚拟节点0，利用桩顶处应变的边界条件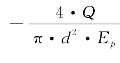：，可将w 0的表达式写为

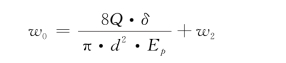
因此可将第一个结点的差分格式写为

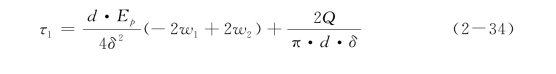
同理，利用虚拟结点n+2和桩底的边界条件，可以得到桩底结点的差分格式，可以写为

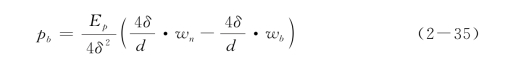
于是，整根桩的位移方程为

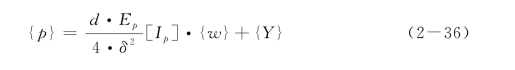
式中：

{p}为各结点处的桩侧摩阻力和端阻力，{p}={p 1　p 2　…　p n　p b}；

{w}为各结点处的竖向位移，{w}={w 1，w 2，…，w n，w b}T；

{Y}为各结点处的竖向荷载，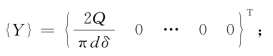

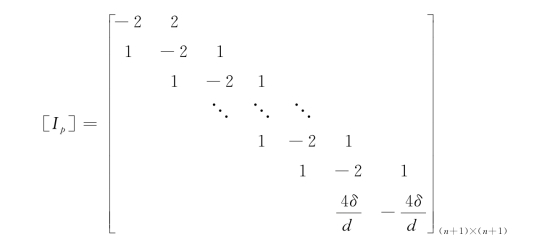
B.土体平衡方程

如图2-8所示，根据n个单元，建立土体的位移方程：

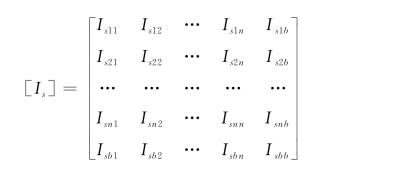
式中，Es为土体弹性模量；[Is]为土体竖向位移柔度矩阵；Isij为[Is]中第i行第j列元素，即当z为i点的埋深，hm1为j点埋深时，则j点作用单位荷载在i点引起的竖向位移。层状地基中，Isij可以通过式(2-38)和式(2-39)求解：

当z(i)＜z(j)时：

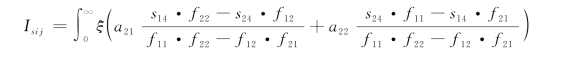
式中：

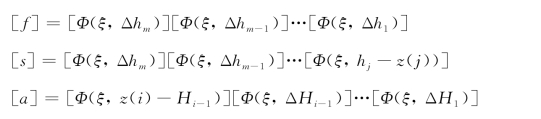
其他量意义参见第一节。当z(i)≥z(j)时：

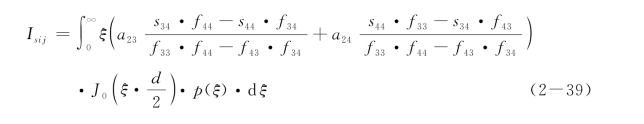
式中：

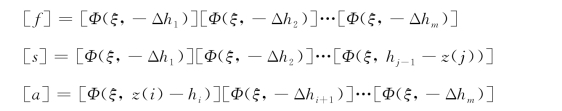
其他量意义参见第一节。

经组装可得

C.整体平衡方程

最后，将式(2-36)和式(2-37)联立，可以得到单桩的整体差分方程：

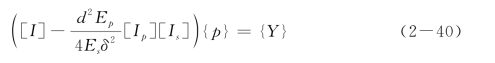
式中，[I]为单位矩阵。

通过式(2-40)求出桩周阻力{p}之后，可以求出桩身位移{w p}及桩身附加轴力。

2.水平向单桩计算方法

如图2-8所示，同样把桩分成n个单元，δ=L/n。以桩侧阻力为未知量，分别取桩周土和单桩建立节点的位移方程，根据桩土之间的位移相容条件，建立平衡方程，解得桩身各节点处的阻力，然后可求出各节点处的位移。

A.桩身平衡方程(www.xing528.com)

单桩桩身的分析采用等间距的差分格式，建立桩身平衡方程。桩身的位移控制方程：

式中，u为桩身结点的竖向位移，q为桩侧阻力，I p为桩截面惯性矩。

从桩顶起，对于第2个至第n个单元，可以写出：

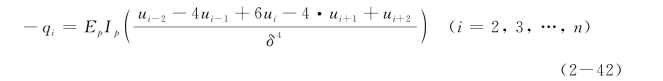
对于第一个单元，引入虚拟节点0和-1，利用桩顶处应变的边界条件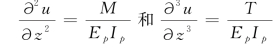：，可将u 0和u-1的表达式写为

因此可将第一个结点和第二个结点的差分格式写为

同理，利用虚拟结点n+2和n+3以及桩底的边界条件，可以得到结点n和n+1的差分格式，可以写为

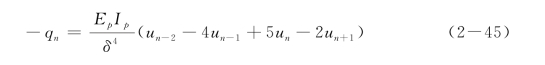
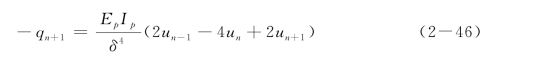
于是，整根桩的位移方程为

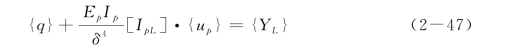
式中：

{q}为各结点处的水平向阻力，{q}={q 1　q 2　…　qn+1}T

{u}为各结点处的水平位移，{u p}={u 1　u 2　…　u n+1}T

{Y L}为各结点处的水平荷载，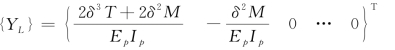

B.土体平衡方程

根据差分方法，土体的位移方程可表示为

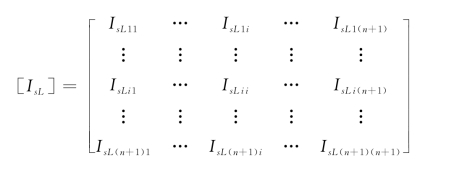
式中，[Is L]为土体竖向位移柔度矩阵；IsLij为[Is L]中第i行第j列元素，即当z为i点的埋深，h m1为j点埋深时，则j点作用单位荷载在i点引起的水平位移，层状地基中，IsLij可以通过式(2-49)求解：

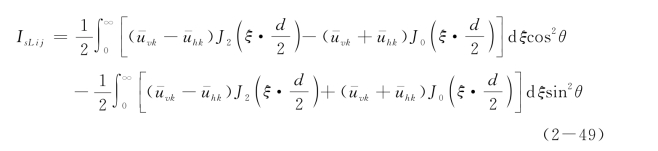
θ为i点和j点的连线和x轴的夹角。

当z(i)＜z(j)时：

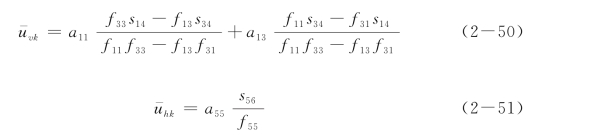
式中：

其他量意义参见第2.1节。

当z(i)≥z(j)时：

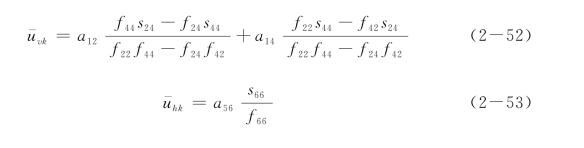
式中：

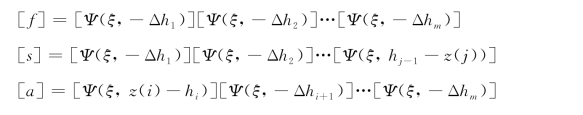
其他量意义参见第2.1节。

经组装，可得

C.整体平衡方程

最后，将式(4-30)和式(4-31)联立，可以得到单桩的整体差分方程：

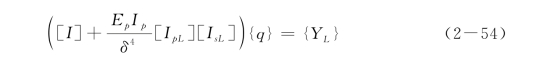
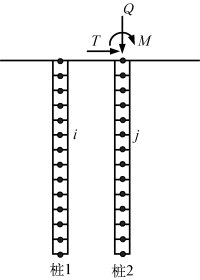
图2-9　桩桩相互作用　计算示意图

式中，[I]为单位矩阵。

通过式(2-54)求出桩周水平阻力{q}之后，可以求出桩身水平位移{u p}及桩身转角和附加弯矩。