数值积分方法在分层地基中的应用

层状体系中，轴对称和非轴对称问题基本解计算式中的积分，都是贝塞尔函数与域内的指数函数乘积的无穷积分问题。其计算方法一般采用Gauss近似积分法，分段累加进行求解。因为是无穷积分，因此需要合理地确定积分的上限，在不增加计算量的情况下保证计算精度；因为包含贝塞尔函数和贝塞尔函数的乘积，因此需要对积分区间的划分进行合理考虑；此外，公式中还包括指数的乘积项，当ξ增大时，这些项可能会溢出，因此需要对指数函数的乘积项进行处理。以下分别给予阐述。

1.含Bessel乘积项的处理与积分区间的确定

零阶和一阶Bessel函数是无穷交错级数，Gauss积分点或为正，或为负，因此，计算时，必须选择Bessel函数的零点为分隔点，对于乘积项的积分区间，需要选择乘积项的零点，如图2-5所示。先在每个分段上积分，再叠加，有

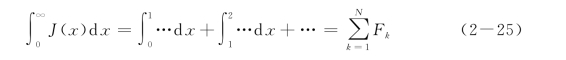
Bessel函数的零点坐标可由查表确定。积分区间段数N的选取与要求的计算精度有关。如果规定的积分精度为[ε]，则N可由下式确定：

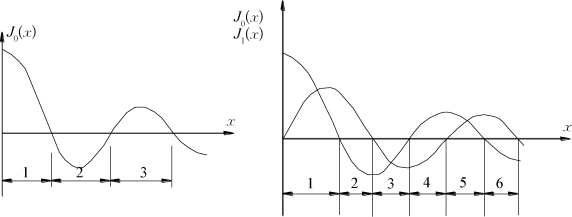
图2-5　Bessel函数的零点积分分隔

金波(1994)建议取10个积分区间，而陆建飞(2001)则认为取20个积分区间才能达到比较精确的结果。本书计算时，采用20个积分区间。此外，当计算点和力的作用点比较近时，积分收敛速度比较慢，陆建飞(2000)、梁发云(2004)采用了欧拉变换来加速收敛。其基本思路为：假定Bessel函数J n(ξr)的零点为η0，η1，η2，…，ηm，…，则相应的积分可写为

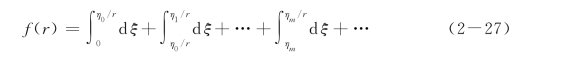
上式可以表示为

式中，(www.xing528.com)

从第m项开始做欧拉变换，则上式可表达为

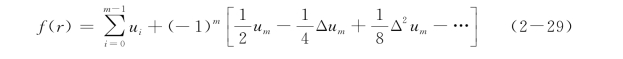
上式中，Δu m=u m+1-u m，Δ2u m=u m+2-2u m+1+um，在实际程序编制中，取m=10。

2.含指数函数乘积项的处理

在矩阵[f]、[a]、[s]等都含有eξΔHi的乘积项，为了防止指数项增大引起溢出，必须对这部分被积函数进行处理。处理的方法是在被积函数的分子分母同时除以e2ξΔHn，以多层地基内部作用一竖向集中力时的竖向位移w为例，根据式(2-8)

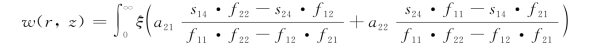
上式经过处理后，成为

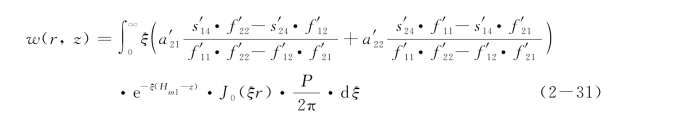
其中，

经过上述处理后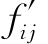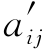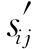，、、等函数均不含指数大于零的项，而且当计算点和荷载作用点不在同一深度时，还存在收敛因子e-ξ(Hm1-z)，所以，计算机实现时，具有较高的计算精度。其他公式亦可按照相同的方式进行处理。