分层地基中开挖对桩筏基的影响分析

1.非轴对称荷载作用下单层地基的传递矩阵法

对于非对称荷载作用，首先对层状弹性半空间中的位移和应力分量进行如下变换：

然后对各位移和应力分量进行傅里叶展开，如下：

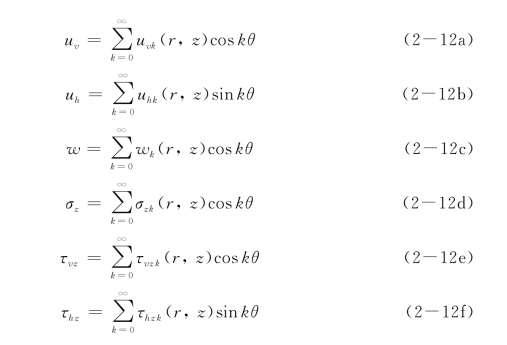
其中，

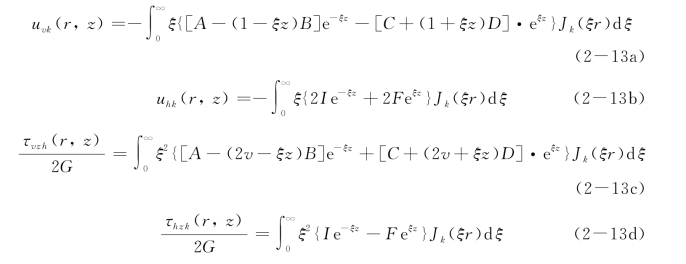
对u vk、σzk、w k、u hk、τvz k、τhzk进行k阶Hankel变换，可得

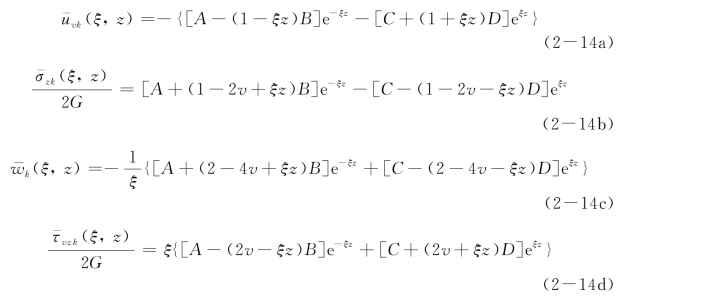
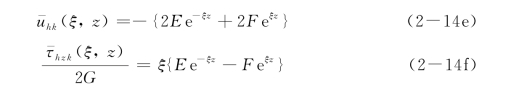
同样，利用z=0的边界条件可以获得系数A、B、C、D、E和F，可以列出均质地基中非对称问题基本解的传递矩阵方程：

其中，

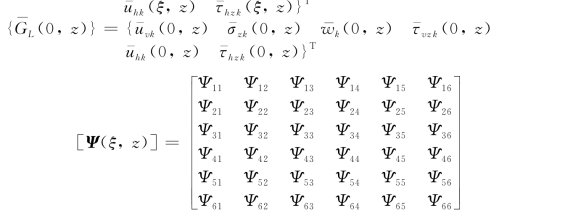
矩阵中各项如下：

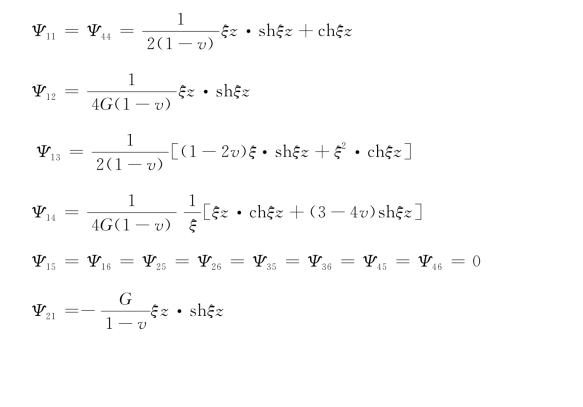
2.非轴对称荷载作用下多层地基解析解

在弹性层状半空间内部作用一个非对称荷载如图2-4所示。荷载沿r、θ和z方向的分量可以表示为，p(H m1，r，θ)、t(H m1，r，θ)和q(H m1，r，θ)。对荷载项傅里叶展开可以表示如下：

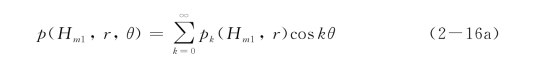
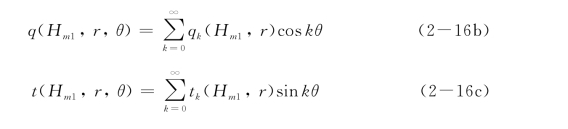
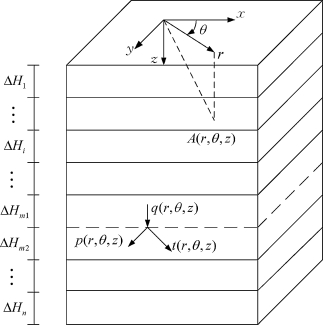
图2-4　多层地基内部作用非轴对称荷载

在地基表面处，即z=0处，自由边界情况：

在地基底面处，即z=H n处，固定边界情况：

根据层间连续条件，运用传递矩阵法，写出每层地基的传递方程：(www.xing528.com)

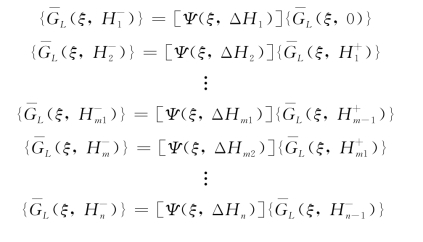
式中，ΔH m1=H m1-H m-1，ΔH m2=H m-H m1，H m1是荷载作用面到地表的距离。

对层间结合条件，进行k阶Hankel变换可得到：

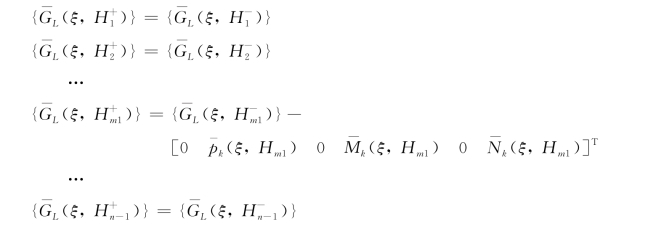
因此，按照层间结合条件，逐层递推，可得

其中，[f]=[Ψ(ξ，ΔH n)][Ψ(ξ，ΔH n-1)]…[Ψ(ξ，ΔH 1)]

[s]=[Ψ(ξ，ΔH n)][Ψ(ξ，ΔH n-1)]…[Ψ(ξ，ΔH m2)]

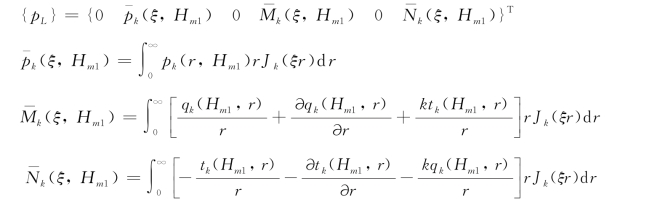
对荷载作用面以上的点：

其中，[a]=[Ψ(ξ，z-H i-1)][Ψ(ξ，ΔH i-1)]…[Ψ(ξ，ΔH 1)]

对于荷载作用面以下的点：按照相同的思路，可以建立与式(2-17)、式(2-18)相似的式子如下：

其中，[f]=[Ψ(ξ，-ΔH 1)][Ψ(ξ，-ΔH 2)]…[Ψ(ξ，-ΔH n)]

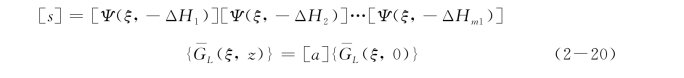
其中，[a]=[Ψ(ξ，z-H i)][Ψ(ξ，-ΔH i+1)]…[Ψ(ξ，-ΔH n)]

由式(2-18)和式(2-20)通过k阶Hankel反变换和合适的积分方法即可求得轴对称荷载作用下式(2-15)中六个等效位移分量值。

由式(2-11)可得

对式(2-21)进行变换，可以得到

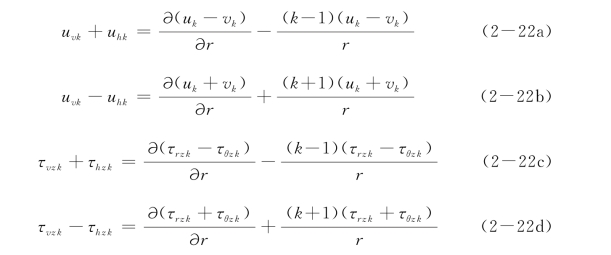
对式(2-22)进行k阶Hankel变换，可得

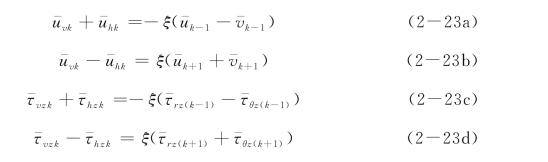
进行k-1阶和k+1阶Hankel反变换，则可以得到

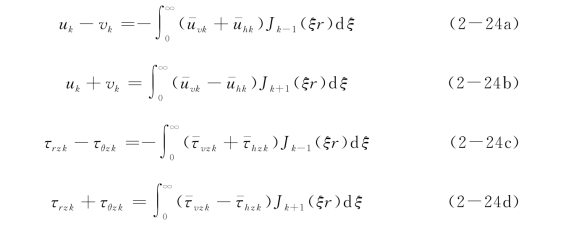
通过坐标变换，可以得到层状弹性半空间中作用非对称荷载时任意点的位移和应力。