Terzaghi(1943)、Casper(1952)、Barnaby(1975)、Milligan(1983)、Peck(1969)等人通过试验研究,并将有支护围护墙和重力式挡土墙墙后土体位移作了对比,研究了基坑开挖周边土体的移动机理。
Caspe(1952)提出了多支撑围护墙后的土体位移模式,将墙后的土体分成三个区:(a)塑性区;(b)弹性区;(c)非扰动区。各区界线为对数螺旋线,其起点分别为基底和墙趾。
Peck(1969)认为,坑后地表沉降大小主要受地区土层条件的控制,并给出地表沉降、离基坑距离、基坑最大深度三者之间的关系曲线。此外,Peck(1969)根据美国芝加哥、挪威奥斯陆等地的现场地表观测资料,提出对不同土层分析墙后地表沉降和沉降范围的经验关系曲线以及相应的经验估算方法。
Lambs(1970)定性地分析了影响坑外土层变形的各种因素,并归纳为八个方面:①基坑长度、宽度和深度;②土的工程性质;③地下水条件;④基坑暴露时间;⑤支撑系统;⑥开挖和支撑顺序;⑦邻近结构和设施;⑧活荷载。
Bransby(1975)给出了有多支护柔性围护墙后土体的位移分布模式,他把整个墙后变形区域划分为五个区,并给出了各自的范围。
Mana和Clough(1981)通过对几个黏性土中开挖工程现场观测资料的分析发现,在普通的施工条件下,墙体最大侧向位移与基坑的抗隆起安全系数存在着某种确定的关系。并结合有限元计算和工程经验提出了稳定安全系数法,用于估算围护结构和墙后地面的最大位移值。
Clough和Hansen(1981)利用有限元模拟分析了土层各向异性对土体、墙体位移分布的影响,指出土体的各向异性将使计算出的墙体位移和地表沉降会显著地增大,破坏区域也会显著增大。
Thomas(1981)通过对大量实测数据和模型试验结果的比较,得出墙体位移与地表沉降的变化规律,认为,墙体位移与地面沉降之比的极限值对于支撑式围护结构的基坑,约为0.6,而对于悬臂式围护结构的基坑,则为1.6。
Milligan(1983)提出,在平面应变状态下主动区位移的简单速度场可用滑移线来形象表示,滑移线与最大主应力方向成45°-φ/2,式中,φ为土体的内摩擦角。
曾国熙(1988)、Tsui(1989)、Wang(1989)、刘国彬(1990)等研究了支撑刚度、挡墙刚度、开挖形状和土的力学性质等对土体沉降的影响,总结了一些关于基坑形状、连续墙的设计尺寸等具体因素对土体沉降影响的规律。
侯学渊和陈永福(1989)根据地表沉陷和墙体水平位移相关的原理并基于三角形沉降公式的思路,提出了基坑地层损失法的概念,采用杆系有限元法或弹性地基梁法,然后依据墙体位移和地面沉降二者的地层移动面积相关的原理,求出墙后地面沉降。
Clough和O'Rourker(1990)统计了基坑维护墙侧向最大变形的值的影响因素,并提出基坑变形控制设计的简化方法,图1-2为简化方法中维护墙水平变形和基坑围护结构刚度之间的关系图。
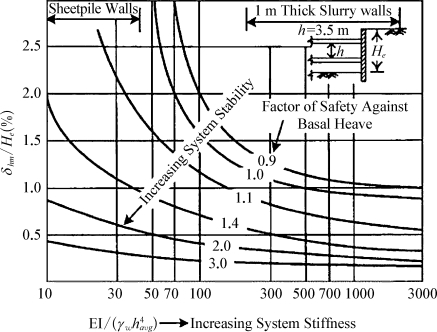
图1-2 围护墙最大侧向位移设计图(https://www.xing528.com)
李佳川(1992)利用三维有限元对钢支撑地下连续墙围护结构的基坑工程的坑周土体位移场进行了计算,并研究了坑底土体位移场的分布规律。
Ou和Hsieh等(1993)通过台北的10个基坑工程变形的实测数据统计,找出了地表沉降与墙体变形的关系,指出开挖引起的地表沉陷型态有凹槽型及三角槽型两种,最大墙体变形与最大地表沉降的比值处于0.5~1.0之间。将地表沉降范围分为主要沉降区和次要沉降区,并给出了基坑围护墙中部(可看做平面应变状态)截面处的地表沉降槽公式。
韩云乔(1996)通过对南京地区一百多个基坑(深度6米以上)开挖后对周围环境影响的调查和监测资料分析,讨论了基坑开挖后的地层移动机理及其影响因素。
李亚(1999)对地层补偿法进行了修正,对于软黏土,简单位移场可表示为δx=δy=f(x+y),引入了收缩系数α,并给出了位移场曲线部分的土体位移表达式。
杨国伟(2000)对超载作用下的基坑墙后地表沉降进行了研究。分析了超载的大小、超载埋置深度、抗隆起安全系数、挡墙变形性态等因素对地表沉降的影响,对地层补偿法进行了修正。
吕少伟(2001)对基坑实测位移场的研究发现,围护墙后土体水平位移分布模式主要可以分为两个区:一个是块体滑动区,该区水平边界距离围护墙大约为1/3倍挖深,垂直边界约为地表下一倍挖深,该区内土体水平位移沿水平方向基本不变,呈现整体滑动的特性;另一个是线性递减区,该区水平边界距离地下墙大约是一倍挖深,垂直边界约为两倍挖深,该区内土体水平位移沿水平方向线性递减到零。另外,地下墙后土体垂直位移分布模式大致也可以分为两个区:一为整体沉降区,开挖面以上至地表范围内的土体沉降值沿深度近似相等,各深度处沉降曲线近似等于地表沉降曲线;二为线性递减区,开挖面以下至两倍开挖深度处,土体沉降值随深度增加,逐渐线性减小为零。
高文华(2002)通过对软土基坑现场位移监测资料的统计分析及数值分析,详细探讨了不同的分步开挖工况条件下坑底和坑周的地层移动规律。
Finno和Roboski(2005)通过对芝加哥基坑的实测资料的分析,分析了基坑周边土体位移规律,指出墙后土体变形的三维分布规律,并提出了经验公式。
Blackburn和Finno(2007)通过对芝加哥某基坑的实测指出,坑后土体变形具有明显的三维效应,并发现三维效应会使墙后土体变形明显减小。
Finno等(2007)通过三维有限元模拟了150个不同尺寸的基坑,指出平面模型能够有效模拟基坑围护墙中部的土体变形,而对于基坑边角的变形,只有在进行三维数值模拟的时候才能有效地估计。
Kung等(2007)通过对不同地区的基坑变形的统计,提出了计算基坑维护墙变形和墙后土体最大沉降的简化计算方法。
Kung等(2009)考虑土体小应变特性,通过对台北某基坑的数值模拟,指出土体的小应变对基坑周边土体变形具有重要的意义。
Wang等(2010)通过对上海软土中300例基坑墙体位移和墙后土体沉降的统计,分析了软土中深基坑开挖引起的土层变形规律。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




