混凝土结构防倒塌评估方法

在偶然荷载作用下，框架梁的主要构件的破坏所导致的整个结构的连续倒塌并不是简单的静力作用过程，而是一个复杂的动力效应作用过程。关键柱失效后所引起的不平衡重力荷载使结构运动并产生动能，要使结构不发生倒塌，就必须把这个动能转化为结构的应变能，从而减缓结构向下的速度。

框架结构在支撑构件失效之后倒塌过程可简化为如图4-32所示的单自由度弹簧体系。在结构的运动过程中，导致结构的动能发生改变，以及由于结构的变形产生应变能。由于结构阻尼耗能远远小于其他耗能，所以忽略阻尼耗能。所以在支撑构件失效后，结构体系的总能量在各个运动阶段都保持守恒，即结构的重力势能、应变能、动能三者是守恒的，如式（4-3）（4-4）所示。

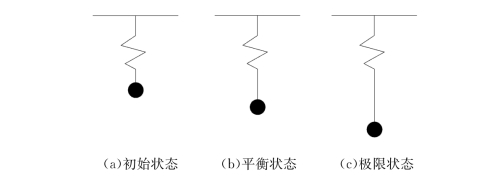
图4-32　单自由度弹簧体系

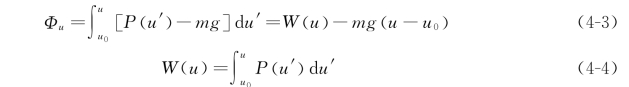
式中，W u（）为结构变形能，通过试验的力与位移关系积分可得；Φu 为当支撑柱位移为u 时所减小的势能。

RC框架结构防倒塌子结构的非线性抗力曲线可取图4-33所示的强化型非线性模型。考虑到线性静力设计时结构抗力需满足与不平衡重力荷载G 的力平衡条件，所以结构屈服抗力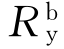＞G，因此结构防倒塌子结构的静力抗力需求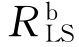在其抗力曲线的线性段（图4-33中A点）。由力平衡关系可得结构防倒塌子结构的线性静力抗力需求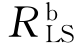=G。

图4-33中的C 点位移为结构变形能力极限，即防倒塌子结构的非线性动力解的上限。根据能量平衡原理，防倒塌子结构还需满足能量平衡关系，即结构的耗能（四边形OBCD 包围的面积）等于结构不平衡质量的势能差（四边形OEED 包围的面积）。因此由能量平衡方法可得框架结构防倒塌子结构非线性动力抗力需求R bND与相应的非线性动力结构位移ΔbND的关系为

式中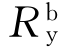， 为防倒塌子结构的屈服抗力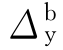； 为防倒塌子结构的屈服位移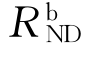；为防倒塌子结构的动力抗力需求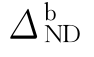；为防倒塌子结构的动力位移响应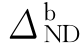， 取图4-33中C 点的位移。

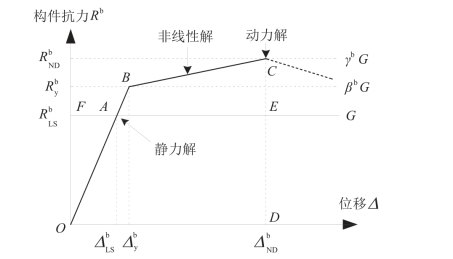
图4-33　结构抗力需求

定义防倒塌子结构的屈服系数为(www.xing528.com)

由式（4-5）和式（4-6）可得结构防倒塌子结构的动力抗力需求为

由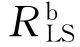=G，可得到防倒塌子结构非线性动力抗力需求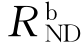与其线性静力抗力需求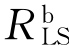间的关系γb 为

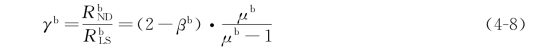
其中，μb=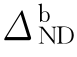/ 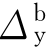为防倒塌子结构的非线性变形系数。防倒塌子结构的极限变形能力决定了其非线性动力结构位移需求 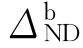的最大值，此时结构的最大非线性变形系数即为结构的延性系数。

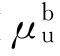因此，框架结构防倒塌子结构的最低承载力储备需求为

由于结构初始设计时已满足线性静力要求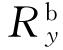 ＞G =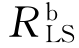，所以有βb ＞1；若βb ≥2，其解则为线性动力抗力需求，因此1＜βb ＜2，即0＜2-βb ＜1。在设计中可偏保守地取

RC 框架结构通过非线性静力Pushdown分析得到结构的防连续倒塌最大抗力，而结构的线性静力抗力需求是1倍竖向重力荷载，两者之比即为结构的防连续倒塌承载力储备实际值γb。当结构的防连续倒塌承载力储备实际值大于等于结构防连续倒塌最低承载力储备需求（γb）min时，即γb≥（γb）min时，结构可满足防连续倒塌要求；反之，若γb＜（γb）min，则不满足防连续倒塌要求。