混凝土结构防连续倒塌设计方法与数值模拟研究

（1）MARC纤维模型建模。

纤维模型按照结构的轴心定位，梁柱节点部分留出刚域，尺寸取梁柱节点尺寸。并假定节点部分刚度大，将其设置为弹性材料。每根柱除刚域外的部分平均分成4段纤维单元，梁平均分成6段纤维单元。完成的纤维模型如图2-18所示。

图2-18　纤维模型示意图

纤维模型中不考虑墙，将板考虑成有效翼缘，梁板结构转换成T 形梁后再进行数值模拟，有效翼缘宽度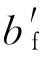按独立梁取值。

（2）钢筋及混凝土的本构参数修改。

钢筋与混凝土的本构参数需要进一步修正，考虑不同因素的影响。

①埋入混凝土的纵向钢筋的应力-应变关系修正。

在很多数值模拟研究中都使用普通钢筋的应力-应变曲线当作钢筋的本构参数，以此来研究混凝土内的钢筋受力情况，然而嵌于混凝土内纵向钢筋的应力-应变本构关系与普通钢筋的本构是不同的。实际上，在混凝土开裂后，混凝土在裂缝处的应力降为零，此时混凝土裂缝处的纵向钢筋应力达到最大。另外，在混凝土裂缝相邻处，即混凝土未开裂完好的区域，混凝土和钢筋之间还存在另一种受力形式，即混凝土与钢筋共同受力，混凝土也会提供抗拉强度。在两种受力形式的共同作用下，当混凝土裂缝之间的钢筋达到屈服时，混凝土完好区域内的钢筋未达到屈服，此时整体钢筋的平均应变还没有达到普通钢筋的屈服应变标准，如果采用普通钢筋的本构关系，即认为整体钢筋的平均应变达到屈服强度时为屈服，就会高估钢筋的承载能力贡献。为了考虑该因素的影响，采用Be1arbi A和Hsu T的双曲线模型修正钢筋抗拉的屈服应力和屈服应变[32]，图形如图2-19，公式如下所示：

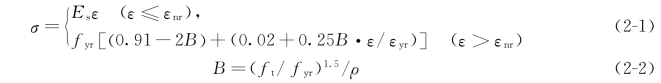
式中，σ，ε，Es分别为嵌入混凝土的纵向钢筋应力、应变、弹性模量；εyr为普通钢筋的屈服应变；εnr 为修正后的屈服应变。

代入ε=εnr，可得εnr=εyr（0.93-2B）/（1-0.25B），参数B 中的ft，fyr，ρ分别表示混凝土的抗拉强度、钢筋的屈服强度和纵向钢筋的配筋率，其中配筋率取比值，即若配筋率为0.6%，计算时取数值0.006。

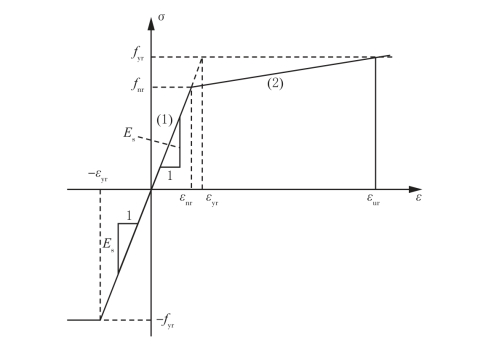
图2-19　嵌入混凝土的钢筋应力-应变曲线

②钢筋混凝土的黏结滑移效应。

钢筋和混凝土之间的黏结滑移效应容易发生在梁柱节点处，由Pan W H 等提出的考虑了钢筋锚固变形的修正版应力-应变曲线[33]，目前使用于很多数值模拟研究中。如图2-20所示，可以看出该模型考虑了梁柱节点处钢筋受拉时的锚固变形。另外，由于钢筋的锚固变形在钢筋受拉的弹性及塑性阶段均有影响，因此在修正曲线中减小了弹性模量，并延长了塑性阶段。

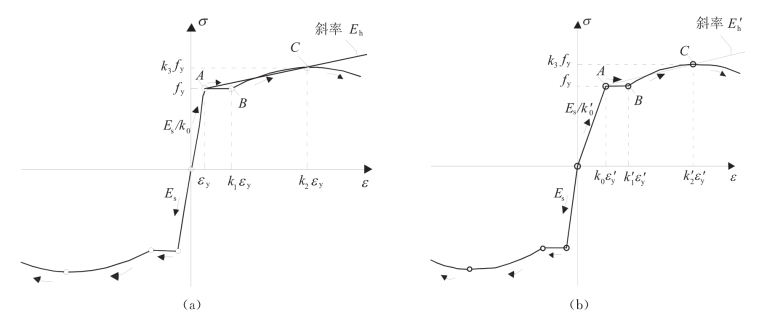
图2-20　钢筋应力-应变曲线

图2-20中的系数计算公式如下所示：

(www.xing528.com)

式中，k1为钢筋的硬化起点应变与屈服应变的比值；k2为钢筋的峰值应变与屈服应变的比值；k3为钢筋的峰值强度与屈服强度的比值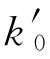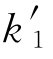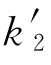；，， 分别为确定修正后的应力-应变曲线的系数；ay，ash分别为钢筋弹性阶段和强化阶段内的应变增大系数；slipy，slipsh分别为钢筋弹性阶段和强化阶段内的总滑移；fy为屈服应力；εy为屈服应变；db 为钢筋直径；ub 为粘着应力，钢筋弹性阶段ub=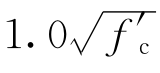，非弹性阶段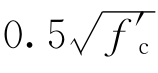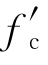，=；为混凝土抗压强度；Le 为梁或柱的纤维单元尺寸。

③混凝土箍筋约束影响。

Park R等提出了一个考虑了箍筋约束造成混凝土强度增强的改良模型[34]，用放大系数K 乘以Kent and Park模型[35]中的峰值应力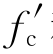和峰值应变0.002，如图2-21所示，达到峰值应力后，应力-应变关系变为下降段的直线线性曲线，曲线可用公式（2-8）和（2-9）表示。本节当达到极限压应变εcu时，应力比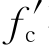减少80%，即fcu=0.2K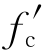，参数K 用公式（2-11）计算。

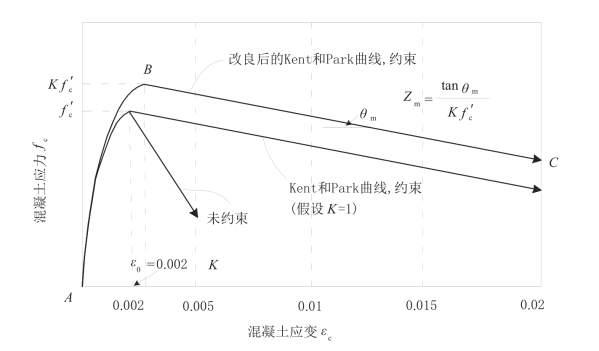
图2-21　Park等改良后的KentandPark曲线

AB 段曲线：

BC 段曲线：

其中：

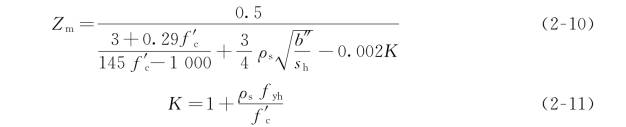
式中，ε0为修正后的峰值应变；ρs为箍筋体积除以混凝土体积的比值，混凝土体积按照从箍筋外围到混凝土中心的体积范围计算；fyh为横向钢筋（箍筋）的屈服强度；f′c为混凝土峰值应力（单位：MPa）；b″为混凝土中心到箍筋外围的宽度；sh为箍筋间距。

当Zm确定后即可用公式（2-13）计算极限压应变εcu：

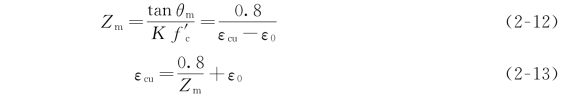
总结如下：

a.混凝土内纵向钢筋的应力-应变：降低钢筋的屈服强度和屈服应变，强化阶段的峰值强度和峰值应变不变，极限强度和极限应变不变。

b.钢筋的黏结滑移：钢筋本构曲线整体向右平移，弹性模量降低，屈服强度、峰值强度及极限强度不变，屈服应变及峰值应变增大，极限应变不变。

c.混凝土箍筋约束作用：混凝土弹性模量不变，峰值强度及峰值应变增大，极限强度取峰值强度的20%，根据公式算出极限应变。