城市热环境与空间形态耦合分析及设计

基于南京新街口中心区80组地表温度参数及形态指标因子，用最小二乘法做地表温度与建筑密度、容积率、平均高度、平均天空可视度、植被覆盖率和不透水面面积比原始数据的多元线性回归，得到回归方程：

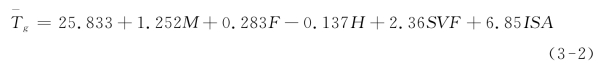
式中: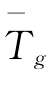——平均地表温度，单位℃；

M——建筑密度，单位%；

F——容积率；

H——平均高度，单位m；

SVF——平均天空可视度；

ISA——不透水面面积比，单位%。植被覆盖率由于同建筑密度和不透水面面积之比间存在相关性，多元线性回归计算中将该指标进行了移除。

由于地表温度与建筑密度、容积率、平均高度原等始数据的数量级和单位存在差异，上式中的各指标的回归系数难以反映影响程度的差异，因此本书将各组数据进行标准化处理，将其转化为无纲量的纯数值，便于各指标能够进行比较。本书数据标准化采用离差标准化方法，对原始数据进行线性变换，使结果映射到［0，100］区间，其计算公式如下：

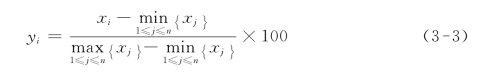
式中:——该数据集中的最大值；——该数据集中的最小值，则标准化的数据y1，y2，…，yn∈［0，100］。

将80组数据按照离差标准化方法标准化后，再利用最小二乘法做多元线性回归，得到回归方程：

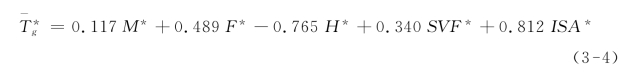
式中自变量与因变量都为标准化后数值，该回归方程的判定系数R2为0.578，说明样本的回归效果一般；F检验的统计量F=20.287，相伴概率值P＜0.001，说明五个自变量与因变量存在线性回归关系。(www.xing528.com)

多元线性回归效果一般，主要可能存在以下的原因：①本节所用的80个街区南京新街口中心区夏季正午时刻热环境模拟结果，每个区块的热环境会受到周边地块形态的影响，因此并不是区块内部建筑空间单一的影响结果；②本节仅对建筑密度、平均高度、平均天空可视度等六项存在明显线性相关的指标因子作了多元线性回归分析，还有部分指标未纳入考虑，同时区块单元的建筑布局、组合方式对热环境也存在较大影响，但并未进行指标量化描述。

但通过多元线性回归分析，我们还是可以进一步验证地表温度与建筑密度、容积率、平均高度、天空可视度、不透水面面积比存在显著的线性关系，其中，与不透水面面积比存在较为强烈的相关性关系。并且，从数据标准化后所得的回归方程（式3-4）中可以看出几个指标因子的影响程度依次应为：不透水面面积比＞天空可视度＞建筑密度＞容积率＞平均高度。

将标准化后的不透水面面积比、天空可视度、建筑密度、容积率、平均高度代入回归方程（式3-4），将所得值与标准化后的平均地表温度进行比较，如图3-29所示，可以看出部分区块的两个数值十分接近，但也有部分街区两个数值相差较大。将同一区块的两个数值相减取绝对值得到图3-30，差值的绝对值越小则说明两个数值的耦合度越高，差值的绝对值越大则说明两个数值的耦合度越低。

图3-29　回归方程（式3-4）计算所得值与标准化后的平均地表温度的比较

＊资料来源：作者自绘

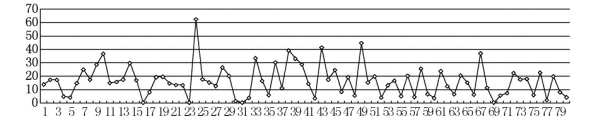
图3-30　回归方程（式3-4）计算所得值与标准化后的平均地表温度差值的绝对值

＊资料来源：作者自绘

运用同样的方法以空气温度作为因变量，同上述六项指标进行多元线性回归分析得到以下方程：

该回归方程的判定系数R2为0.151，说明样本的回归效果一般；F检验的统计量F=2.64，相伴概率值P=0.30，说明五个自变量与因变量的线性回归关系较弱。

通过耦合分析我们发现，由于模拟的初始条件仅是夏季中午这一特定时期，模拟区域也仅仅是城市中心区，耦合结果并不显著，生成的公式不能被作为预测其他案例的普世性公式。为了获得一般预测公式，应进行更多样本更长时间的模拟。从这个方面而言，本项目仅仅是一个初步的研究，只展示下研究方法。