园林基础工程：简单计算园林土方量

土方量的计算一般是根据附有原地形等高线的设计地形来进行的。根据精确程度要求，可分为估算和计算。在规划阶段，土方量的计算无需太过精细，粗略估计即可。而在作施工图时，土方工程量则要求精确计算。计算土方量的方法很多，常有的大致有三种：估算法、断面法和方格网法。

1.估算法

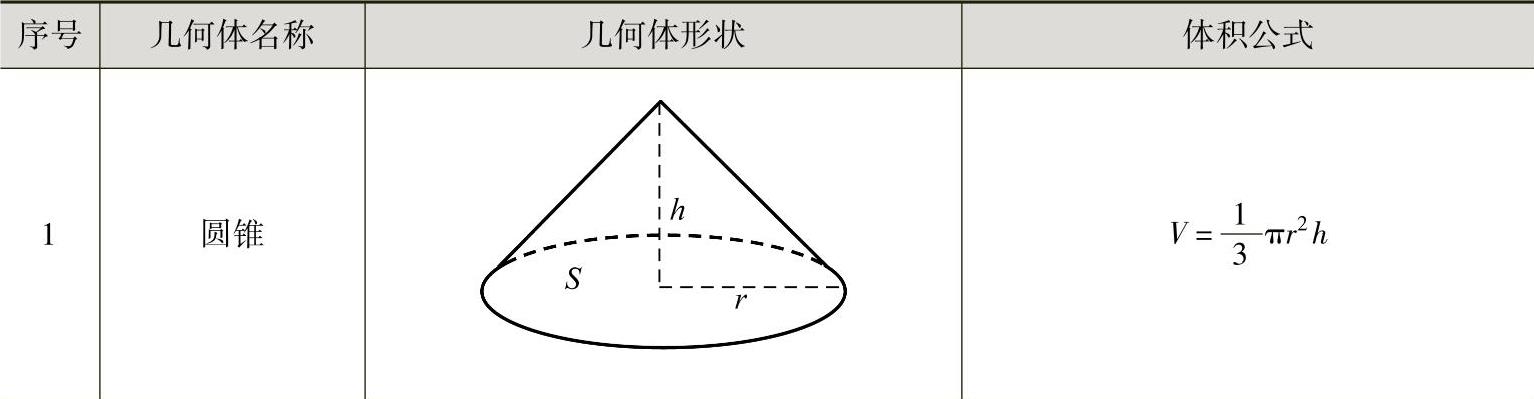
体积公式估算法就是把设计的地形近似地假定为锥体、棱台等几何形体的地形单体，这些地形单体可用相近的几何体体积公式来计算见表2-2。该方法简便、快捷，但精度不够。

表2-2 体积公式估算土方工程量

（续）

注：V—体积；r—半径；S—底面积；h—高；r₁、r₂—上、下底半径；S₁、S₂—上、下底面积

2.断面法

断面法是以一组等距（或不等距）的相互平行的截面将拟计算的地块、地形单体（如山、溪涧、池、岛等）和土方工程（如堤、沟渠、路堑、路槽等）分截成“段”，分别计算这些“段”的体积，将各段体积累加，以求得该计算对象的总土方量。用此方法计算土方量时，精度取决于截取的断面的数量，多则较精确，少则较粗略。

断面法可分为垂直断面法、等高面法与水平面成一定角度的成角断面法。

（1）垂直断面法。垂直断面法多用于园林地形纵横坡度有规律变化地段的土方工程量计算，计算较为方便。其计算方法如下：

1）用一组相互平行的垂直截断面将要计算的地形截成多“段”，相邻两断面之间间距一般用10m或20m，平坦地区可大些，但不得大于100m，如图2-4所示。

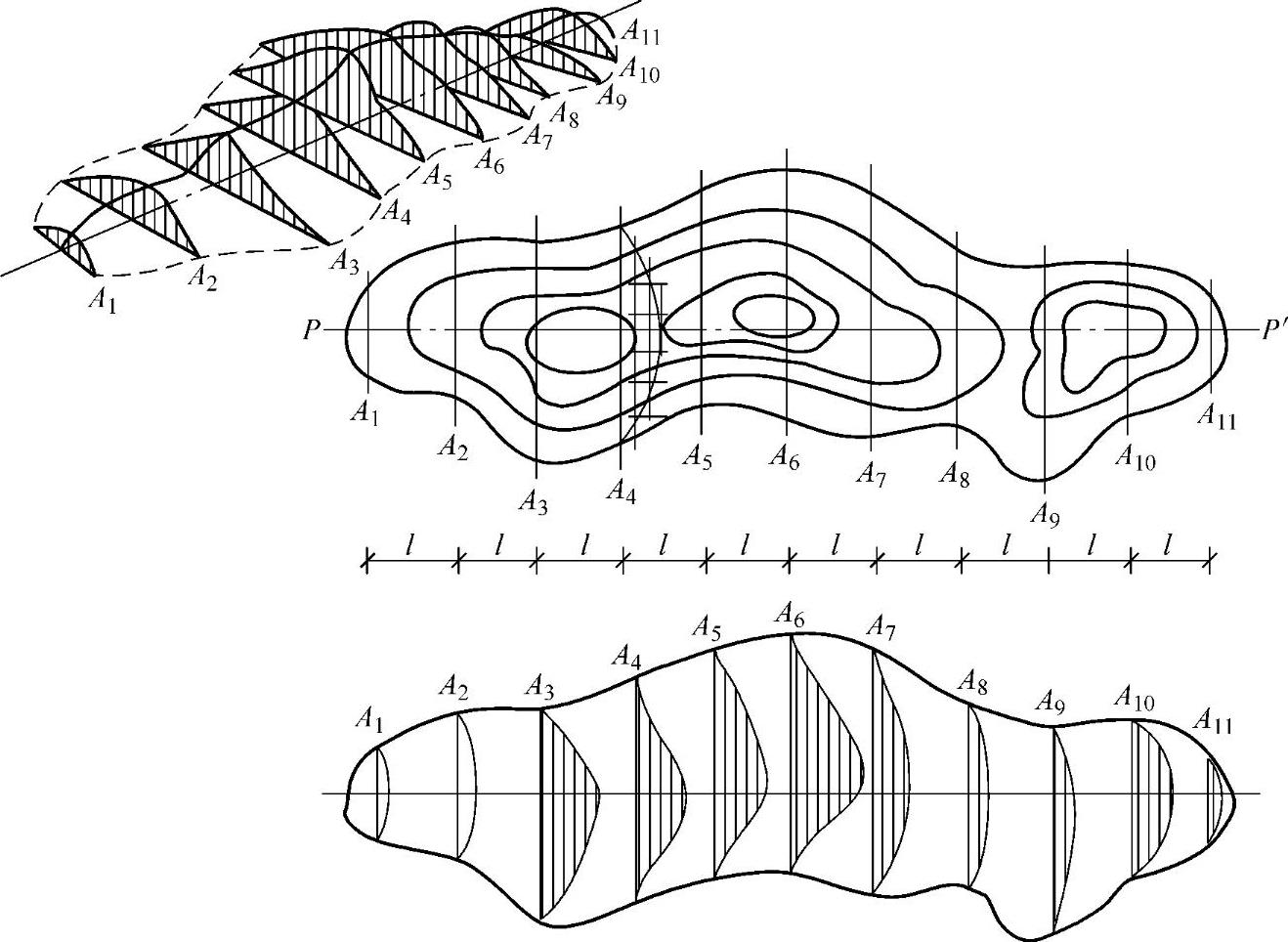
图2-4 带状土山垂直断面取法

2）分别计算每个“段”的体积，把各“段”的体积相加，即得总土方量，公式为：

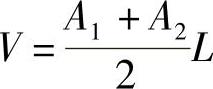
式中 V——相邻两断面的土方量（m³）；

A₁，A₂——相邻两横断面的挖（或填）方断面面积（m²）；

L——相邻两横断面的间距（m）。

（2）等高面法。等高面法又称为水平断面法，是沿等高线取断面，等高距

即为两相邻断面的高差，计算方法同断面法。等高面法最适于大面积的自然山水

地形的土方计算。我国园林向来崇尚自然，园林中山水布局讲究，地形的设计要

求因地制宜，充分利用原地形，以节约工力。同时为了造景又要使地形起伏多

变。总之，挖湖堆山的工程是在原有的崎岖不平的地面上进行的。所以计算土方

量时必须考虑到原有地形的影响，这也是自然山水园土方计算较繁杂的原因。由

于园林设计图样上的原地形和设计地形均用等高线表示，因而采用等高面法进行

计算最为方便，如图2-5所示。

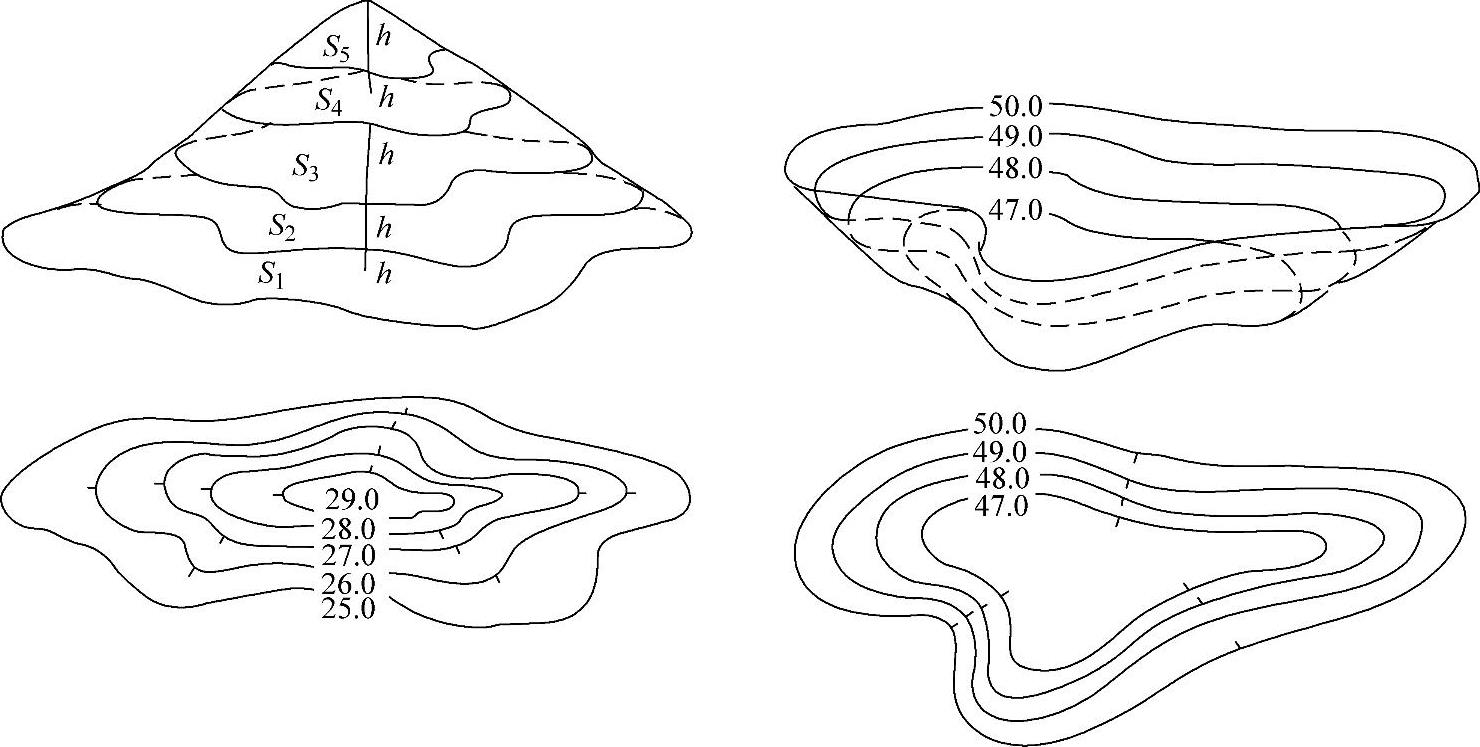
图2-5 等高面法图示

其体积计算公式如下：(www.xing528.com)

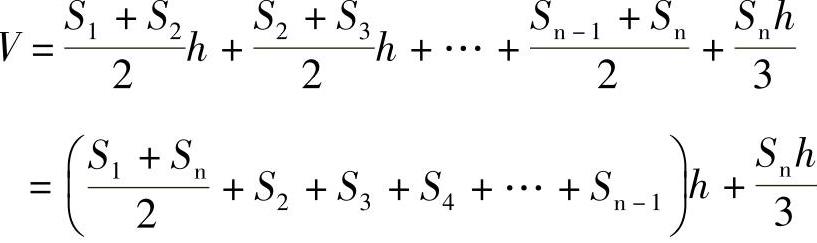
式中 V——土方体积（m³）；

S——断面面积（m²）；

h——等高距（m）。

3.方格网法

方格网法是把平整场地的设计工作与土方量计算工作结合在一起进行的，用方格网计算土方量相对比较精确，一般用于平整场地，其基本工作程序如下：

（1）划分方格网。根据已有地形图将场地划分成若干个方格网，尽量与测量的纵、横坐标网对应，将相应设计标高和自然地面标高分别标注在方格点的右上角和右下角。将自然地面标高与设计地面标高的差值，即各角点的施工高度（挖或填）填在方格网的左上角，挖方为（+），填方为（-），用插入法求得原地形标高，如图2-6所示。

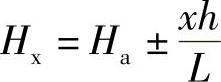
式中 H_x——角点原地形标高；

H_a——低边等高线的高程；

x——角点至低边等高线的距离；

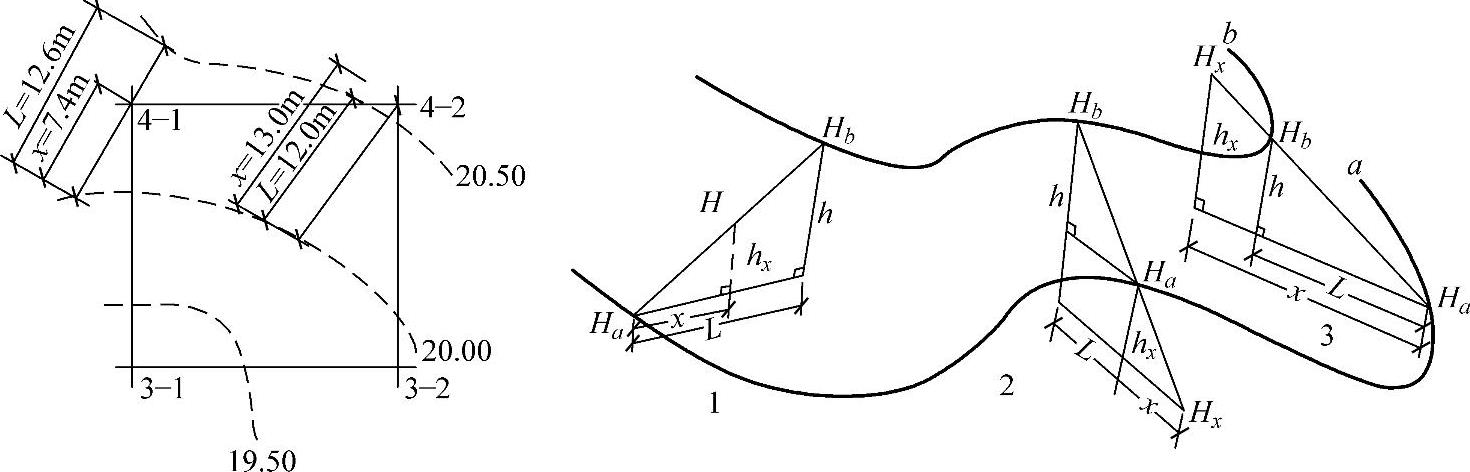
图2-6 插入法求任意点的高程（单位：m）

h——等高差；

L——相邻两等高线间最短距离。插入法求高程通常会遇到的三种情况。当待求点标高H_x在两等高线之间时：

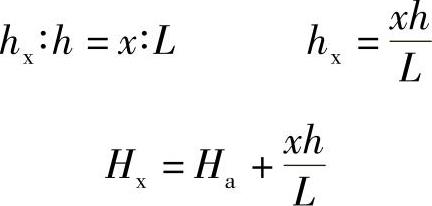
当待求点标高H_x在低边等高线H_a的下方时：

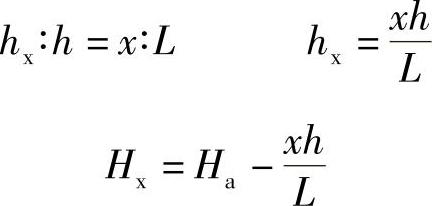
当待求点标高H_x在高边等高线H_b的上方时：

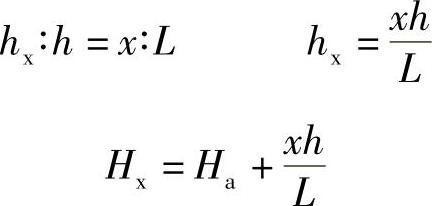
（2）计算零点位置。零点即不挖不填的点，零点的连线就是零点线，在一个方格网内同时有挖方或填方时，一定有零点线，应计算出方格网边上的零点的位置，并在方格网上标注出来，连接零点即得填方区与挖方区的分界线，即零点线。零点的位置按下式计算：

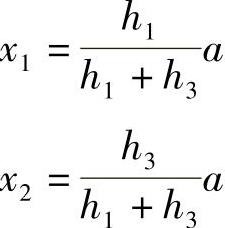
式中 x₁，x₂——角点至零点的距离（m）；

h₁，h₂——相邻两角点的施工高度（均用绝对值）（m）；

a——方格网的边长（m）。

（3）土方量计算。根据方格网中各个方格的填挖情况，分别计算出每一方格的土方量，几种相应的计算图及计算公式见表2-3。计算出每个方格的土方工程量后，再对每个网格的挖方、填方量进行合计，算出填、挖方总量。

表2-3 方格网计算图及计算公式

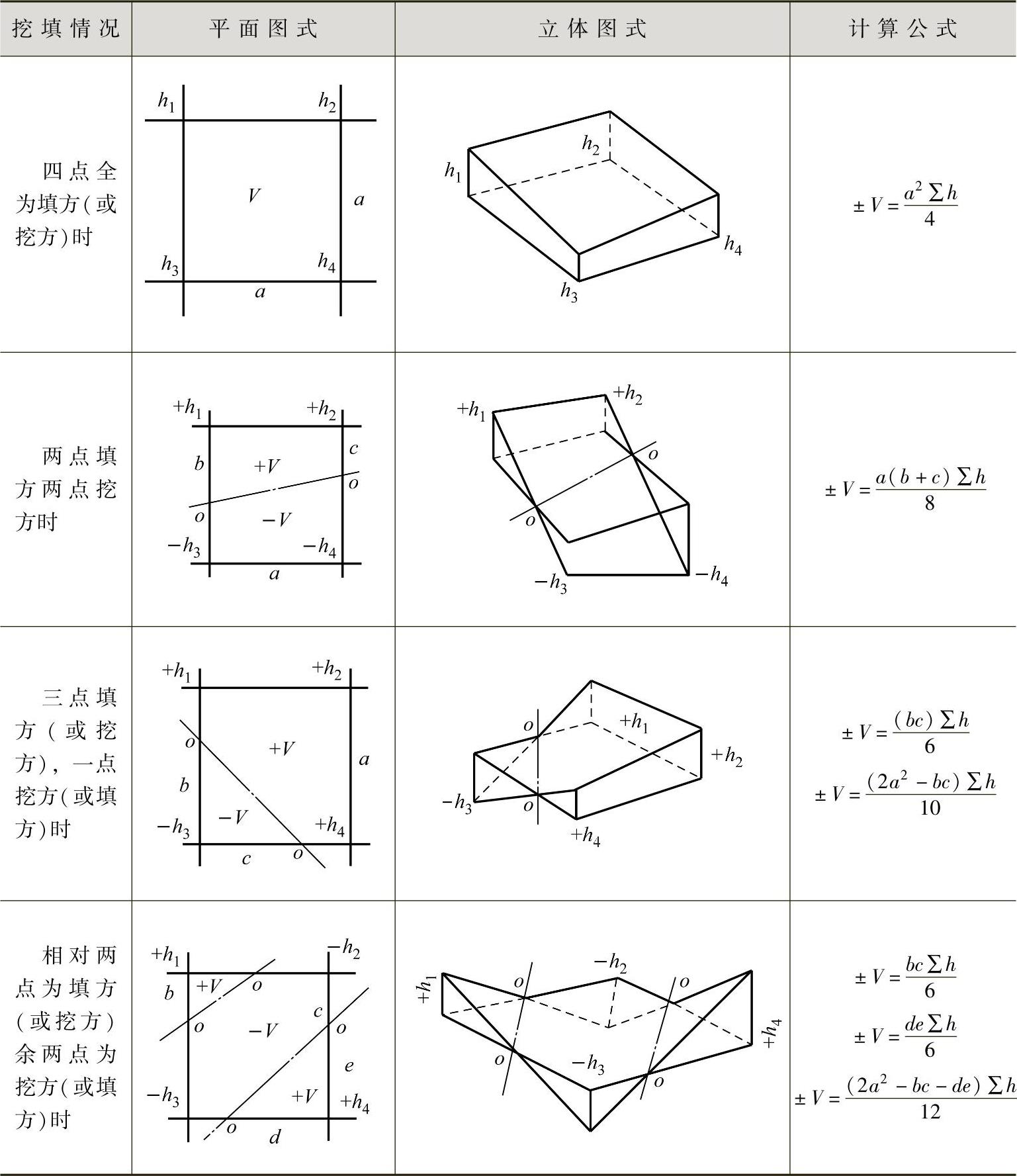
注：计算公式中的“+”表示挖方，“-”表示填方。