实践技能-正投影基本性质解读

正投影的基本性质有全等性、积聚性和类似性。

1.全等性

在图1-29中，空间直线AB平行于投影面H，作A和B两个端点在H面上的正投影a和b。连接ab即得AB直线在H面上的正投影。由于AB平行于H面，即有Aa=Bb，因而有ABba为矩形，故得ab=AB。同理可推出：当△CDE平行于H面时：它在H面上的正投影△cde全等于△CDE。分析得出结论：当空间直线或平面平行于投影面时，其在所平行的投影面上的投影反映了直线的实长或平面的实形，正投影的这种性质称为全等性。

2.积聚性

在图1-30中，空间直线AB垂直于投影面H，由于直线AB与投射线方向一致。作直线AB在H面上的正投影时，很容易得出直线AB在H面上的正投影重叠为一点a（b）。同理可推出，当△CDE垂直于H面时，其在H面上的正投影为一条积聚的直线cde。通过以上分析，得出：当直线或平面垂直于投影面时，它在所垂直的投影面上的投影为一点或一条直线。正投影的这种性质称为积聚性。

3.类似性

在图1-31中，空间直线AB倾斜于投影面H，它在H面上的正投影ab显然比AB短，但ab仍是一直线。△CDE倾斜于投影面，它在H面上的正投影为△cde。同样也可以想象出，当空间为n边的平面图形与投影面倾斜时，其投影仍为n边形，只是大小与空间n边形不全等而已。通过以上分析，得出：当空间直线或平面倾斜于投影面时，它在该投影面上的正投影仍为直线或与之类似的平面图形，其投影的长度变短或面积变小，这一性质称为类似性。(www.xing528.com)

图1-29 正投影全等性的演示

图1-30 正投影积聚性的演示

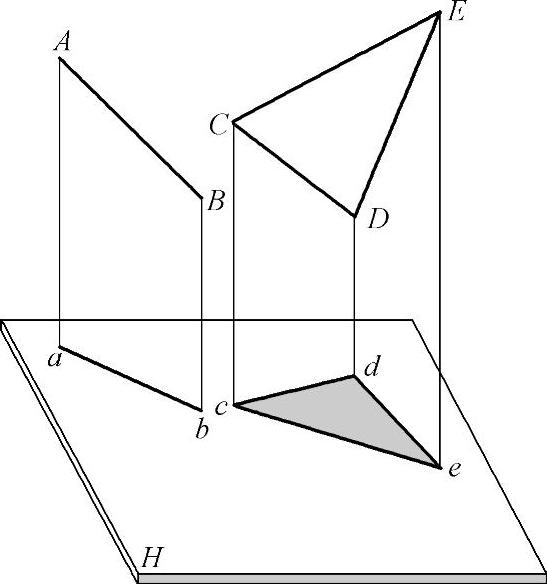
图1-31 正投影类似性的演示