SOC估计算法：常用算法及应用

（1）开路电压法

开路电压法是根据电池的开路电压（Open Circuit Voltage，OCV）与电池内部锂离子浓度之间的变化关系，间接地拟合出它与电池SOC之间的一一对应关系。在进行实际操作时，需要将电池充满电量后以固定的放电倍率（一般取1C）进行放电，直到电池的截止电压时停止放电，根据该放电过程获得OCV与SOC之间的关系曲线。当电池处于实际工作状态时便能根据电池两端的电压值，通过查找OCV-SOC关系表得到当前的电池SOC。开路电压法与放电试验法一样，并不适用于运行中的电池SOC估算。图5.11所示为某动力电池组电压与容量的关系。

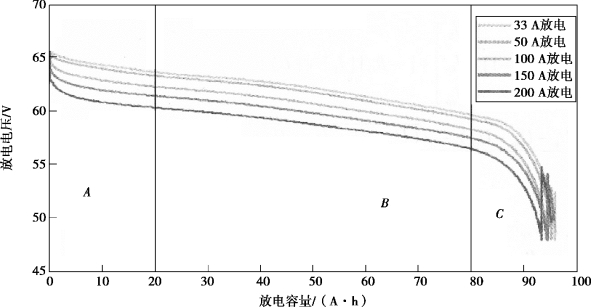
图5.11　某动力电池组电压与容量的关系

（2）容量积分法

容量积分法是通过对单位时间内，流入流出电池组的电量进行累积，从而获得电池组每一轮放电能够放出的电量，确定电池SOC的变化。

（3）电池内阻法

电池内阻有交流内阻（常称交流阻抗）和直流内阻之分，它们都与SOC有密切关系。准确测量电池单体内阻比较困难，这是直流内阻法的缺点。在某些电池管理系统中，通常将内阻法与Ah计量法组合使用来提高SOC估算的精度。

（4）模糊逻辑推理和神经网络法(www.xing528.com)

模糊逻辑接近人的形象思维方式，擅长定性分析和推理，具有较强的自然语言处理能力；神经网络采用分布式存储信息，具有很好的自组织、自学习能力。神经网络法适用于各种电池，其缺点是需要大量的参考数据进行训练，估计误差受训练数据和训练方法的影响很大。它们的共同特点是：均采用并行处理结构，可从系统的输入、输出样本中获得系统输入输出关系。

神经网络法是模拟人脑及其神经元用以处理非线性系统的新型算法，无须深入研究电池的内部结构，只须提前从目标电池中提取出大量符合其工作特性的输入与输出样本，并将其输入使用该方法所建立的系统中，就能获得运行中的SOC值。该方法后期处理相对简单，即能有效避免卡尔曼滤波法中需要将电池模型做线性化处理后带来的误差，又能实时地获取电池的动态参数。但是神经网络法的前期工作量比较大，需要提取大量且全面的目标样本数据对系统进行训练，所输入的训练数据和训练的方式方法在很大程度上都会影响SOC的估计精度。此外，在电池温度、自放电率和电池老化程度不统一等因素的复杂作用下，长期使用该方法估算同一组电池的SOC值，其准确性也会大打折扣。因此，在动力电池的SOC估算工作中该方法并不多见。

（5）卡尔曼滤波法

卡尔曼滤波法的核心思想是对动力系统的状态做出最小方差意义上的最优估算。其适用于各种电池，不仅可以给出SOC的估计值，还可以给出SOC的估计误差。其缺点是电池SOC估计精度越高，电池模型越复杂，涉及矩阵运算越多，工程上越难以实现。另外，该方法对于温度、自放电率以及放电倍率对容量的影响考虑得不够全面。

卡尔曼滤波法是美国数学家卡尔曼（R.E.Kalman）在20世纪60年代初发表的论文《线性滤波和预测理论的新成果》中提出的一种新型最优化自回归数据滤波算法。该算法的本质在于可以根据最小均方差原则，对复杂动态系统的状态做出最优化估计。非线性的动态系统在卡尔曼滤波法中会被线性化成系统的状态空间模型，在实际应用时系统根据前一时刻的估算值与当前时刻的观测值对需要求取的状态变量进行更新，遵循“预测—实测—修正”的模式，消除系统随机存在的偏差与干扰。使用卡尔曼滤波法估算动力电池的SOC时，电池以动力系统的形式被转化为状态空间模型，SOC则变成为该模型内部的一个状态变量。建立的系统是一个线性离散系统。

卡尔曼滤波法不仅能够修正系统初始误差，还能有效地抑制系统噪声，因此在运行工况非常复杂的电动汽车动力电池的SOC估算中具有显著的应用价值。不过该方法同样存在两个缺陷：其一，卡尔曼滤波法估算SOC的精度很大程度上取决于电池模型的准确程度，工作特性本身就呈高度非线性化的动力电池，在卡尔曼滤波法中经过线性化处理后难免存在误差，如果模型建立得不够准确，其估算的结果也并不一定可靠；其二，该方法涉及的算法非常复杂，计算量极大，所需要的计算周期较长，并且对硬件性能要求苛刻。

（6）放电试验法

放电试验法是将目标电池进行持续的恒流放电直到达到电池的截止电压，将此放电过程所用的时间乘以放电电流值，即作为电池的剩余容量。该方法一般作为电池SOC估算的标定方法或者用在蓄电池的后期维护工作上，在不知道电池SOC值的情况下采用此方法，相对简单、可靠，并且结果也比较准确，同时对不同种类的蓄电池都有效。