【摘要】:②直线通过属于平面的一点,且平行于平面内的另一条直线,则直线属于此平面。图2.23平面上直线的几何条件在已知平面△ABC的投影图中求取属于平面的直线的作图法,如图2.24所示。已知K点属于△ABC,还知K点的V面投影k′,求作K点的水平投影k。先在△a′b′c′内过投影k′任作一直线m′n′,然后求出其H投影mn,进而求出在mn上的投影k,则投影k一定属于投影△ABC。
1)属于平面的直线
直线属于平面的几何条件为:
①直线通过属于平面上的两个点,则该直线属于此平面,如图2.23(a)所示中的直线MN,BM。
②直线通过属于平面的一点,且平行于平面内的另一条直线,则直线属于此平面。如图2.23(b)所示中的直线L,其通过平面上的点A,且平行于平面内的直线BC,因此该直线属于△ABC。

图2.23 平面上直线的几何条件
在已知平面△ABC的投影图中求取属于平面的直线的作图法,如图2.24所示。

图2.24 在平面的投影图上取线
①图为先取属于平面△ABC的两点M(m′,m),N(n′,n),然后分别连接直线m′n′,mn,则直线MN一定属于平面△ABC的。
②图为过△ABC平面上一点A(可为平面上任意一点),且平行于△ABC的一条边BC(b′c′,bc)作一直线L(l′,l),则直线L一定属于平面△ABC。(https://www.xing528.com)
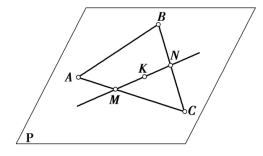
图2.25 平面上点的几何条件
2)属于平面的点
点属于平面的几何条件为:点属于平面的任一直线,则点属于此平面,如图2.25所示。
取属于平面的点,只有先取属于平面的一条直线,再取属于直线的点,才能保证点属于平面。否则,在投影图中不能保证点一定属于平面。
在已知平面△ABC的投影图中求取属于平面的点的作图法,如图2.26所示。
已知K点属于△ABC,还知K点的V面投影k′,求作K点的水平投影k。先在△a′b′c′内过投影k′任作一直线m′n′,然后求出其H投影mn,进而求出在mn上的投影k,则投影k一定属于投影△ABC。即K点一定属于平面△ABC,如图2.26(b)所示。
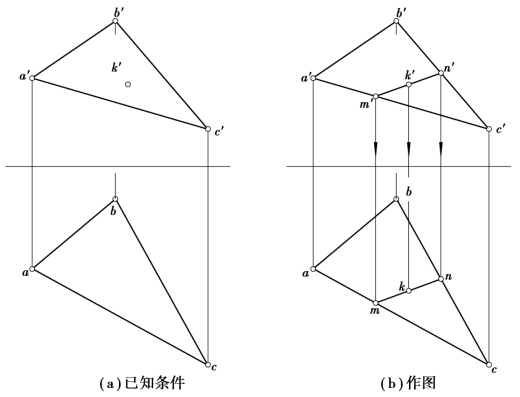
图2.26 平面的投影图上取点
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




