1)一般位置直线的投影特性
与H,V,W 3个投影面均倾斜(即不平行又不垂直)的直线称为一般位置直线,简称一般直线。如图2.17(a)中AB就是一般位置直线,AB与H,V,W面的倾角分别为α,β,γ。图2.17(b)表示一般位置直线AB的三面投影图,其投影特性如下:
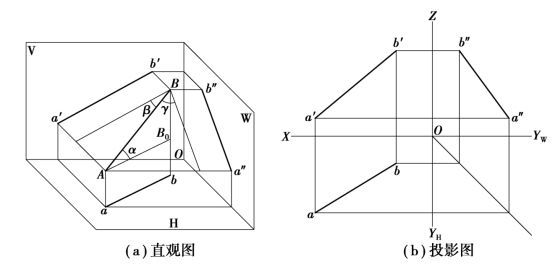
图2.17 一般位置直线
①一般直线在3个投影面上的投影均倾斜于投影轴。
②各投影与投影轴的夹角不能反映直线AB对投影面的真实倾角。
③各投影的长度均小于直线AB的实长,分别有:ab=ABcos α;a′b′=ABcos β;a″b″=AB cos γ(α,β,γ为0°~90°)。
2)一般位置直线的实长和倾角
由于一般位置直线对3个投影面的投影都是倾斜的,故3个投影均不反映该直线的实长及其对投影面的倾角,但可以根据直线的投影,用图解的方法来进行求解。下面用直角三角形法来解决一般位置直线实长及倾角的求法。
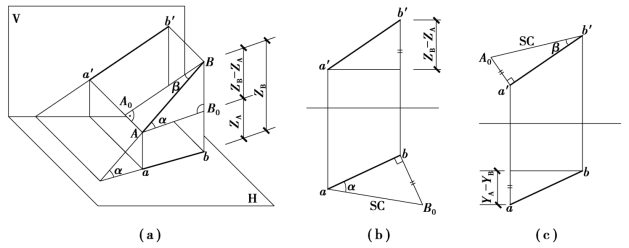
图2.18 求一般位置直线AB的实长及倾角
如图2.18(a)所示,AB为一般位置直线,在AB与其水平投影ab所决定的平面ABba内,过点A作AB0//ab,与Bb相交于B0点。由于Bb⊥ab,所以AB0⊥BB0,△AB0B是直角三角形。该直角△AB0B中有:斜边AB是实长(用SC来表示实长),∠BAB0=α=直线AB对H面的倾角,AB0=ab=直线的H面投影长度,B0B=Bb-Aa=ZB-ZA(即B,A两点到H面的距离差)。因此,只要作出△AB0B,便可求出一般位置直线AB的实长和对H面倾角α。
同理,过点B作BA0//a′b′,则△AA0B也是直角三角形,亦有:斜边仍是空间直线AB,∠ABA0=β=直线AB对V面的倾角,BA0=a′b′=直线的V面投影长度,AA0=YA-YB(即A,B两点到V面的距离差)。因此,只要作出△AA0B,便可求出一般位置直线AB的实长和对V面的倾角β。
根据上述方法,在投影图中以水平投影ab为一条直角边,然后过b(或a)引ab的垂线,并在该垂线上量取bB0=ZB-ZA,连aB0即为直线AB的实长,aB0与ab的夹角(即bB0边所对的角)便是AB对H面的倾角α,如图2.18(b)所示。
以a′b′为一条直角边,过a′(或b′)作a′b′的垂线,在该垂线上量取a′A0=YA-YB,连A0b′即为直线AB的实长,A0b′与a′b′的夹角便是直线AB对V面的倾角β,如图2.18(c)所示。(https://www.xing528.com)
综上所述,在投影图上求直线的实长和倾角的方法是:以直线在某个投影面上的投影为一条直角边,以直线的两端点到该投影面的距离差为另一条直角边作直角三角形,该直角三角形的斜边就是所求直线的实长,而此斜边与投影的夹角,就是该直线对该投影面的倾角。
以上求一般位置直线的实长和倾角的方法,称为直角三角形法。该直角三角形中包含了实长、距离差、投影和倾角4个参数。四者任知其中二者,即可作出一个直角三角形,从而便可求出其余两个。需要注意的是,距离差、投影、倾角三者是对同一投影面而言。
3)属于直线的点
(1)属于直线的点的投影特性
属于直线的点的投影必在该直线的同面投影上,且符合点的投影规律。
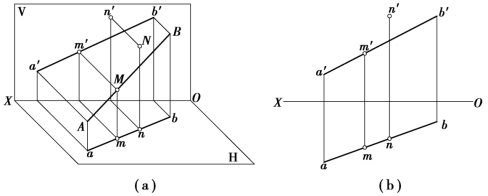
图2.19 属于直线的点的投影
如图2.19(a)所示,直线AB的H面投影为ab,若点M属于直线AB,则过点M的投射线Mm必属于包含AB向H面所作的投射平面ABba,因而Mm与H面的交点M必属于该投射平面与H面的交线ab。同理可知m′必属于a′b′。
反之,如果点的各个投影均属于直线的各同面投影,且各投影符合点的投影规律,即投影连线垂直于相应的投影轴,则该点属于该直线。如图2.19(b)所示中,点M属于直线AB,而点N则不属于直线AB。
(2)点分线段成定比
点分线段成某一比例,则该点的投影也分该线段的投影成相同的比例。
在图2.19(a)中,点M分空间直线AB为AM和MB两段,其水平投影m也分ab为am和mb两段。在投射平面ABba中,直线AB与ab被一组互相平行的投射线Aa,Mm,Bb所截割,则am∶mb=AM∶MB。同理可得:a′m′∶m′b′=AM∶MB和a″m″∶m″b″=AM∶MB。所以,点分直线段成定比,投影后比例不变,即:

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




