建筑制图与识图：点的三面投影

点是构成形体的最基本元素，点只有空间位置而无大小。

1）点的三面投影的形成

把空间点A放置在三面投影体系中，过点A分别作垂直于H面、V面、W面的投射线，投射线与H面的交点a称为A点的水平投影（H投影）；投射线与V面的交点a′称为A点的正面投影（V投影）；投射线与W面的交点a″称为A点的侧面投影（W投影）。

投影的表示方法约定：空间点用大写字母表示（如A），其在H面上的投影用相应的小写字母表示（如a），在V面上的投影用相应的小写字母并在右上角加一撇表示（如a′），在W面上的投影用相应的小写字母并在右上角加两撇表示（如a″）。如图2.11（a）所示，空间点A的H，V，W面投影分别为a，a′，a″。

按前述规定将3个投影面展开，就能得到点A的三面投影图，如图2.11（b）所示。在点的投影图中一般只画出投影轴，不画投影面的边框，如图2.11（c）所示。

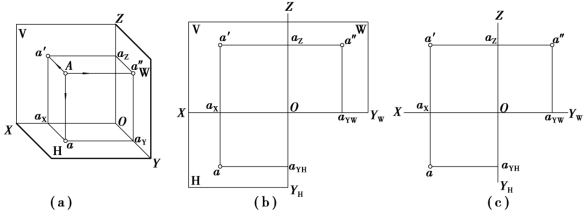
图2.11　点的三面投影

2）点的投影规律

由图2.11（a）可知，过空间点A的两条投影线Aa和Aa′所构成的矩形平面AaaXa′，与V面和H面互相垂直并相交，交线aaX和a′aX与OX轴必然互相垂直且相交于一点aX，OX轴垂直于平面AaaXa′。而aaX和a′aX是互相垂直的两条直线，当V面不动，将H面绕OX轴旋转90°至与V面成为同一平面时，aaX和a′aX就成为一条垂直于OX轴的直线，a′，aX，a三点共线，即aa′⊥OX，如图2.11（b）所示。同理可证，a′a″⊥OZ。aY在投影面展平之后，被分为aYH和aYW两个点，所以aaYH⊥OYH，a″aYW⊥OYW。

通过以上分析，可以得出点的投影规律如下：

（1）点的投影的连线垂直于相应的投影轴

①点的V面投影和H面投影的连线垂直于X轴，即aa′⊥OX。

②点的V面投影和W面投影的连线垂直于Z轴，即a′a″⊥OZ。

③aaYH⊥OYH，a″aYW⊥OYW，aaYH＝a″aYW。

这3项正投影规律，称为“长对正、高平齐、宽相等”的三等关系。

（2）点的投影到各投影轴的距离，分别代表点到相应的投影面的距离

①a′aX＝a″aYW＝Aa，即点的V面投影到OX轴的距离等于点的W面投影到OYW轴的距离，等于空间点A到H面的距离。

②aaX＝a″aZ＝Aa′，即点的H面投影到OX轴的距离等于点的W面投影到OZ轴的距离，等于空间点A到V面的距离。

③a′aZ＝aaYH＝Aa″，即点的V面投影到OZ轴的距离等于点的H面投影到OYH轴的距离，等于空间点A到W面的距离。

3）求点的第三投影(www.xing528.com)

根据上述投影特性可以得出：在点的三面投影图中，每两个投影都具有一定的联系性。因此，只要给出一点的任意两个投影，就可求出其第三投影，并且确定点的空间位置。

如图2.12（a）所示，已知点A的水平投影a和正面投影a′，则可求出其侧面投影a″。

图2.12　求点的第三投影

①过a′引OZ轴的垂线a′aZ，所求a″必在改线延长线上，如图2.12（b）所示。

②在a′aZ的延长线上截取a″aZ＝aaX，a″即为所求，如图2.12（c）所示。

或以原点O为圆心，以aaX为半径作弧找到与OYW轴的交点，过此点作OYW轴的垂线交a′aZ于一点，此点即为a″，如图2.12（d）所示。

也可过a引OYH轴的垂线aaYH，再过aYH作与OYH轴夹角45°的辅助线，过交点作垂线向上交a′aZ于一点，此点即为a″，如图2.12（e）所示。

还可过原点O作45°辅助线，过a引OYH轴的垂线并延长交辅助线于一点，过此点作OYW轴垂线交a′aZ于一点，此点即为a″，如图2.12（f）所示。

4）特殊位置点的投影

①投影面上的点：如空间点位于投影面上，点到该投影面的距离为零（即空间点和该面投影重合），点在另外两个面的投影则位于投影轴上。反之，空间点的3个投影中如有两个投影位于投影轴上，该空间点必定位于某一投影面上。

如图2.13所示，A点位于H面上，则A点到H面的距离为零。其H面投影a与A重合，V面投影a′在OX轴上，W面投影a″在OYW轴上。同理可得，位于V面的B点和位于W面的C点的投影。

图2.13　投影面上的点

②投影轴上的点：如空间点位于投影轴上，点到两个投影面的距离都为零（即空间点和两个面投影重合，且位于投影轴上），点的另外一个投影则与原点O重合。反之，空间点的3个投影中如有两个投影重合且位于投影轴上，该空间点必定位于某一投影轴上。

如图2.14所示，D点位于X轴上，则D点到H面、V面的距离均为零。其H面投影d、V面投影d′都与D重合，W面投影d″与原点O重合。同理可得出位于Y轴的E点和位于Z轴的F点的投影。

图2.14　投影轴上的点