考点剖析:了解抛物线的定义,了解它的标准方程和几何性质;会求抛物线的标准方程,会根据标准方程求焦点坐标、准线方程等,了解抛物线的简单应用.
1.抛物线的定义:平面内到定点F的距离与到定直线l的距离相等的点的轨迹称为抛物线.定点F称为抛物线的焦点,定直线l称为抛物线的准线.
2.抛物线的标准方程、图像及性质如下表所示:
【题型1】抛物线的定义及几何性质
例1 求抛物线x2=-8y的焦点坐标、准线方程、焦点到准线的距离.
解:由题知:-2p=-8,所以p=4,
所以它的焦点坐标是(0,-2),准线方程是y=2,焦点到准线的距离是4.
例2 点A是抛物线x2=4y上一点,它到焦点的距离为13,则点A到准线的距离是多少?
解:因为抛物线上任一点到焦点的距离等于其到准线的距离,所以点A到准线的距离是13.
【锦囊妙计】抛物线焦点随“一次项”走.
赢在起点
1.抛物线x2=-8y的焦点是________________,准线方程是________________,焦点到准线的距离是________________.
2.抛物线y2+16x=0的焦点是______________,准线方程是________________,焦点到准线的距离是________________.
3.抛物线![]() 的焦点是_________________,准线方程是________________,焦点到准线的距离是________________.
的焦点是_________________,准线方程是________________,焦点到准线的距离是________________.
4.点M是抛物线y2=16x上一点,它到准线的距离为20,则点A到焦点的距离是___________,A点的横坐标是___________,纵坐标是___________.
【题型2】求抛物线的标准方程
例1 已知抛物线的顶点在原点,对称轴是x轴,且焦点到准线的距离是6,求该抛物线的标准方程.
解:由题知p=6,所求抛物线的标准方程是y2=12x或y2=-12x.
例2 已知抛物线的顶点在原点,对称轴是坐标轴,且经过A(2,-4),求该抛物线的标准方程.
解:由题意可设抛物线的标准方程是x2=-2py或y2=2p′x
解得![]()
所求抛物线的标准方程是x2=-y或y2=8x.
赢在起点
1.抛物线的焦点是A(3,0),准线方程是x=-3,则抛物线的标准方程是__________.
2.抛物线的焦点是A(0,-2),顶点在原点,则抛物线的标准方程是_____________.
3.焦点在y轴上的抛物线经过A(2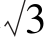 ,2),则抛物线的标准方程是___________.
,2),则抛物线的标准方程是___________.
【题型3】抛物线标准方程的应用
例1 抛物线y2=4x上有一点A,它到焦点的距离为6,求点A的坐标.
解:如图所示,抛物线的焦点坐标是F(1,0),准线l的方程为x=-1,过A作AM⊥l,垂足是M,AM交y轴于N,由抛物线的定义得知![]()
所以![]() ,因而得知A点的横坐标是5,
,因而得知A点的横坐标是5,
把它代入抛物线方程y2=4x,得y=±2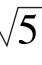 ,
,
所以A的坐标为(5,2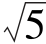 )或(5,-2
)或(5,-2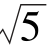 ).
).
例2 已知点A(2,1),F是抛物线y2=4x的焦点,P为抛物线上一点,则![]() 的最小值是多少?
的最小值是多少?
解:如图所示,P为抛物线上任一点,分别过P,A向y轴作垂线,垂足分别为M,M1,因为![]()
在△PAM中,![]()
而![]()
又因为![]()
所以![]()
![]()
即![]()
赢在起点
1.抛物线y2=16x上有一点A,它到焦点的距离为9,则点A到准线的距离是________,点A的横坐标是________,纵坐标是________,所以点A的坐标是____________.
2.抛物线x2=-12y上有一点B,它到焦点的距离为5,则点B到准线的距离是______,点B的纵坐标是______,横坐标是______,所以点B的坐标是____________.
3.抛物线y2=-8x上有一点M,它到焦点的距离为7,则点M的坐标是___________.
【题型4】直线与抛物线的关系
例 已知抛物线的顶点在原点,对称轴为x轴,并且经过点(1,2),
(1)求抛物线的标准方程;
(2)经过抛物线的焦点F且倾斜角为60°的直线l交抛物线于A,B两点,求![]() 的长;
的长;
(3)经过点D(0,4)作直线交抛物线于M,N两点,以线段MN为直径作圆.试问圆能否经过原点?若能,求出此时直线MN的方程;若不能,请说明理由.
解:(1)由题可设抛物线的标准方程为y2=2px,因为过点(1,2),所以22=2p×1,
解得p=2,所以抛物线的方程是y2=4x,
(2)因为抛物线的方程是y2=4x,所以它的焦点F(1,0),
又k=tan 60°=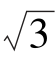 ,由直线的点斜式方程得:y=
,由直线的点斜式方程得:y= (x-1)即
(x-1)即![]()
由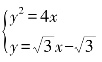 解得
解得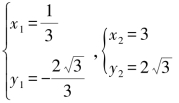
所以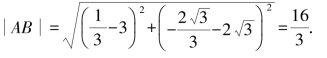
(3)以线段MN为直径作圆能经过原点,理由如下:不妨设MN所在直线的斜率为k,则MN的直线方程为y=kx+4,再设M(x1,y1),N(x2,y2),假设以MN为直径的圆能经过原点,则有∠MON=90°,所以OM⊥ON,kOM×kON=-1,![]()
即 x1x2+y1y2=0
联立解方程组![]() 得
得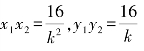
由x1x2+y1y2=0得![]() ,解得k=-1
,解得k=-1
所以MN的直线方程为y=-x+4,即x+y-4=0.
赢在起点
1.抛物线y2=4x的焦点坐标是__________,过焦点的直线其倾斜角(锐角)的正弦值是![]() ,则该直线的斜率是__________,直线的方程是____________,直线与抛物线的交点坐标是_____________________,交点间的距离是__________.
,则该直线的斜率是__________,直线的方程是____________,直线与抛物线的交点坐标是_____________________,交点间的距离是__________.
2.抛物线x2=2y的焦点坐标是________,直线y=kx-3,若直线与抛物线有交点,则斜率k的取值范围是_____________,若k=3,则直线与抛物线相交于两点,这两点的坐标是________________,它们的距离是________,这两点与原点构成了一个三角形,这个三角形的面积是___________.
一、填空题
1.抛物线是平面内到一定点F的距离与它到一定直线l的距离________的点的轨迹.
2.焦点在x轴的正半轴上的抛物线标准方程是____________,其焦点坐标是____________,准线方程是____________.
3.焦点在y轴的负半轴上的抛物线标准方程是____________,其焦点坐标是____________,准线方程是____________.
4.抛物线标准方程中“p”表示的是_________________________________.
5.抛物线y2+8x=0的焦点坐标是____________________.
6.顶点在原点,焦点F(0,-3)的抛物线标准方程是____________________.
7.抛物线方程y2=-16x,则它的焦点到准线的距离是____________________.
8.抛物线方程x2=-4y,则它的准线方程是____________________.
9.抛物线的顶点在原点,准线方程为y=-2,则它的标准方程是____________________.
10.抛物线y2-12x=0的焦点坐标是____________,准线方程是____________________.
11.顶点为坐标原点,焦点到准线的距离为5,且焦点在x轴负半轴上的抛物线标准方程是____________________.(https://www.xing528.com)
12.抛物线y2=20x上一点P,它到焦点的距离是15,则其到准线的距离是__________,它的横坐标是____________,点P的坐标是____________.
二、选择题
1.顶点在原点,准线为x=-2的抛物线方程是( ).
A.y2=8x B.y2=-8x C.x2=8y D.x2=-8y
2.顶点在原点,焦点F(1,0)的抛物线标准方程是( ).
3.顶点在原点,对称轴是x轴且经过点P(-3,2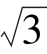 )的抛物线,其标准方程是( ).
)的抛物线,其标准方程是( ).
4.焦点是F(0,-4),准线是y=4的抛物线方程是( ).
A.y2=16x B.y2=-16x C.x2=16y D.x2=-16y
5.对称轴是y轴,焦点到准线的距离为7的抛物线方程是( ).
A.y2=14x B.x2=14y
C.x2=-14y D.x2=14y或x2=-14y
一、填空题
1.对称轴是x轴,且过点P(2,6)的抛物线标准方程是____________________.
2.抛物线x2=16y上有一点Q,它到焦点的距离为9,则它的坐标是____________.
3.已知直线y=2x+b与抛物线y=x2有两个交点,则b的取值范围是_____________.
4.若直线y=2x+m与抛物线y2=4x没有公共点,则m的取值范围是____________.
5.抛物线![]() 的焦点坐标是____________________.
的焦点坐标是____________________.
6.顶点为坐标原点,且经过点M(1,-3),则抛物线的标准方程是____________________.
7.以双曲线![]() 的左顶点为焦点,顶点在原点的抛物线标准方程是_____________________.
的左顶点为焦点,顶点在原点的抛物线标准方程是_____________________.
8.过抛物线x2=-12y的焦点且倾斜角为45°的直线方程是____________________.
9.抛物线y2=-2x与直线x-y+4=0的相交,其交点坐标是____________________.
10.抛物线x2=-4y的焦点到直线3x+4y-5=0的距离是____________________.
二、选择题
1.与平面一定点(-1,0)和定直线x=1的距离相等的点的轨迹方程是( ).
A.x2=2y B.x2=4y C.y2=2x D.y2=-4x
2.直线y=x+1与抛物线x2=4y相交于M,N两点,O为坐标原点,则S△MON=( ).
A.2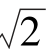 B.4
B.4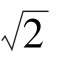 C.
C.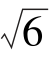 D.2
D.2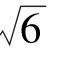
3.过抛物线y2=8x的焦点且与直线x+y-5=0平行的直线方程是( ).
A.x-y-2=0 B.x-y-4=0 C.x+y-4=0 D.x+y-2=0
4.以椭圆![]() 的左焦点为焦点,顶点在原点的抛物线方程是( ).
的左焦点为焦点,顶点在原点的抛物线方程是( ).
A.y2=-12x B.y2=-6x C.x2=-6y D.x2=-12y
5.以C(-2,1)为圆心,经过抛物线x2=4y的焦点的圆的标准方程是( ).
A.(x+2)2+(y-1)2=10 B.(x+2)2+(y-1)2=2
C.(x-2)2+(y+1)2=10 D.(x+2)2+(y-1)2=4
三、解答题
1.在抛物线y2=12x上找一点P,它与焦点的距离为9,求点P的坐标.
2.过抛物线y2=-8x的焦点,且倾斜角为![]() 的直线交抛物线于A,B两点,求:
的直线交抛物线于A,B两点,求:
(1)该直线的方程;
(2)![]()
(3)△OAB的面积.
3.已知抛物线的顶点在原点,对称轴为y轴,焦点坐标F(0,1),
(1)求抛物线的标准方程;
(2)若过点A(0,m),且斜率为2的直线与该抛物线没有交点,求m的取值范围;
(3)过焦点F且与x轴平行的直线与抛物线相交于P,Q两点,求以F为圆心,PQ为直径的圆的方程.
1.已知抛物线的顶点在坐标原点,焦点在y轴上,抛物线上一点M(m,-3)到焦点的距离为5,(1)求m的值;(2)过焦点F作垂直于y轴的直线交抛物线于A,B两点,求A B.
2.已知抛物线x2=-4y,过抛物线的焦点且倾斜角为45°的直线交抛物线于P,Q两点,
(1)求直线PQ的方程;
(2)求直线PQ与坐标轴围成的三角形的面积;
(3)是否存在一条过焦点直线l,当l与抛物线交于A,B点,且以AB为直径的圆经过坐标原点.若存在,求出这条直线的方程;若不存在,说明理由.
自我评价
(满分100分,时间45分钟) 评价结果:__________
一、填空题(每题5分,共50分)
1.椭圆 的焦点坐标为____________________.
的焦点坐标为____________________.
2.椭圆9x2+5y2=45的离心率是____________________.
3.椭圆经过点P(-2,0),且长轴是短轴的2倍,则椭圆的标准方程是________________.
4.已知F1,F2为椭圆![]() 的两个焦点,过F1的直线与椭圆交于A,B两点,则△ABF2的周长是____________________.
的两个焦点,过F1的直线与椭圆交于A,B两点,则△ABF2的周长是____________________.
5.双曲线![]() 上一点到它一个焦点的距离等于1,则该点到另一个焦点的距离等于____________________.
上一点到它一个焦点的距离等于1,则该点到另一个焦点的距离等于____________________.
6.双曲线的焦点在x轴上,其中a=2 5,且经过点(-5,2),则双曲线的标准方程是____________________.
7.双曲线![]() 的两条渐近线方程是____________________.
的两条渐近线方程是____________________.
8.抛物线x2=12y的焦点坐标为____________________.
9.顶点在原点,准线是x=4的抛物线的标准方程是____________________.
10.抛物线4y2-x=0的准线方程是_____________________.
二、选择题(每题5分,共20分)
1.椭圆的![]() 的离心率是( ).
的离心率是( ).
2.椭圆的长轴为6,且长轴在y轴上,离心率为![]() ,则该椭圆的标准方程是( ).
,则该椭圆的标准方程是( ).
3.一个焦点坐标为(0,-10),虚轴长为16的双曲线的标准方程是( ).
4.准线方程为x=2的抛物线的标准方程是( ).
A.y2=-4x B.y2=-8x C.y2=4x D.y2=8x
三、解答题(每题10分,共30分)
1.已知中心在原点的双曲线的一个焦点是F1(-5,0),一条渐近线方程是4x-3y=0,求双曲线方程.
2.有一抛物线型拱桥,当水面距拱顶4米时,水面宽40米,当水面下降1米时,水面宽是多少米?
3.点P是椭圆4x2+5y2=20上的一点,且它在x轴的上方,F1,F2分别为椭圆的左、右焦点,斜率为-1的直线PF2与椭圆交于Q点,M为PQ的中点,求△MF1F2的面积.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




