圆与直线位置关系方程

考点剖析：理解圆与直线相切、相离、相交的充要条件，会正确判定圆与直线的位置关系；能解决圆与直线相交、相切、相离的简单问题.

1.圆与直线的位置关系

设圆的标准方程：（x-a）2+（y-b）2=r2，其中圆心为（a，b），半径为r，圆心到直线的距离为d，有：

2.圆与直线相切中切线长及切线的方程

（1）切线长：

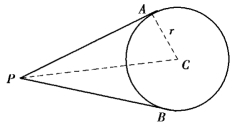
切线长

（2）切线方程：

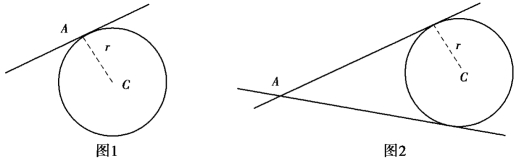
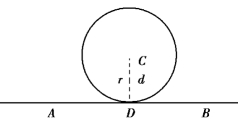
①过圆上一点A的切线方程（图1），通常利用CA与切线垂直，它们的斜率互为负倒数来求切线方程，这时的切线只有一条.

②过圆外一点A的圆的切线方程（图2），通常采用设切线的斜率为k，利用圆心到切线的距离d等于r列方程的方法来求切线方程，这时的切线有两条.

3.圆与直线相交中的弦长问题

在Rt△ACD中，其中弦长

4.圆与直线相离中圆上的某动点到直线的最长（短）距离

圆上的一动点到直线的最长距离是，最短距离是

【题型1】判断圆与直线的位置关系

例　判断直线与圆的位置关系：

（1）直线x-y=0与圆x2+y2=1；

（2）直线y=x+1与圆（x-1）2+y2=2；

（3）直线y=-2x-5与圆x2+y2-4x+3=0.

解：（1）圆心（0，0），圆的半径r=1，则d=0，

由于d＜r，所以直线与圆相交.

（2）圆心（1，0），圆的半径r=，直线方程为x-y+1=0，

则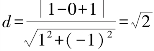，由于d=r，所以直线与圆相切.

（3）圆的方程为（x-2）2+y2=1，圆心（2，0），圆的半径r=1，

直线方程为2x+y+5=0，则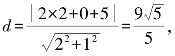

由于d＞r，所以直线与圆相离.

另解：联立解直线与圆的方程组，采用代入消元法，消去得x（或y）得到关于y（或x）一元二次方程，方程的判别式：（1）若Δ＞0，方程组有两组解，则直线与圆有两个交点，所以直线与圆__________；（2）若Δ=0，方程组只有一组解，则直线与圆只有一个交点，所以直线与圆____________；（3）若Δ＜0，方程组没有解，则直线与圆没有交点，所以直线与圆____________.

赢在起点

1.d表示的是________________，若d＜r，则直线与圆________，若d=r，则直线与圆________，若d＞r，则直线与圆________，若d=0，则直线与圆________________.

2.圆（x+3）2+（y-2）2=9，圆心C的坐标是________________，半径r=__________，直线化成一般式是________________，该圆的圆心到直线的距离d=________，则d________r，所以直线与圆的位置关系是____________.

3.（2016年高考题）直线2x+3y+1=0与圆（x+1）2+（y-2）2=4的位置直线是（　）.

A.相离　B.相切　C.相交且过圆心　D.相交但不过圆心

【题型2】直线与圆相离的问题

例　已知M是圆（x+2）2+（y+1）2=1上一动点，求M到直线3x-4y+22=0的最短和最长距离.

解：圆心（-2，-1），圆的半径r=1，过圆心C作直线的垂线交于D，

圆心到直线的距离d=4＞r，所以直线与圆相离，如图所示，最短距离最长距离

赢在起点

已知A是圆（x-2）2+（y+1）2=9上的一动点，则点A距离直线3x+4y+22=0的最远距离是____________，最近距离是___________.

【题型3】直线与圆相切的问题

例1　求过点（2，3）且与圆（x-1）2+（y+1）2=17相切的直线方程.

解：如图所示，因为D（2，3）在圆（x-1）2+（y+1）2=17上，且圆的圆心是C（1，-1），连接CD，则有CD⊥AB，所以

又因为，所以

则直线AB的方程为

即x+4y-14=0.

例2　（2014年高职考试题）已知某圆的圆心为（1，1），且过点（2，1），（1）求该圆的标准方程；（2）求该圆经过点（3，2）的切线方程.

解：（1）圆的半径r=

圆的方程为（x-1）2+（y-1）2=1.

（2）由题知：点（3，2）是圆外一点，设所求圆的切线的斜率为k，则

切线方程可表示为y-2=k（x-3），即kx-y+2-3k=0，

又圆心C到切线的距离为

由于直线与圆相切，所以d=r，则有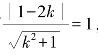

解得k=0或

所求圆的切线方程为y=2或4x-3y-6=0.

注：经过圆外一点与圆相切的切线有两条，如果求出的斜率只有一个，则说明还有一条切线的斜率不存在，这条垂直于x轴的直线方程需补充出来.

【锦囊妙计】有关直线与圆相切的问题通常用d=r来解决.

赢在起点

1.以（2，1）为圆心，且与直线4x-3y+2=0相切的圆的标准方程是________________.

2.过点M（1，-2）且与圆x2+y2=5相切的直线方程是_________________.

3.过点M（3，-2）且与圆x2+y2=9相切的直线方程是___________.

【题型4】直线与圆相交的问题

例　已知：直线x-y-1=0，圆x2+y2=13，（1）求直线与圆的交点；（2）求弦长.

解：联立方程

由②得　y=x-1③

代③入①得　x2-x-6=0

解得

所以交点为（3，2）和（-2，-3），

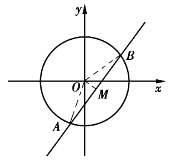
求弦长的另解：如图所示，设直线与圆交于A，B两点，

圆的圆心O（0，0），半径

圆心到直线x-y-1=0的距离

在Rt△AMO中，

所以弦长

赢在起点

1.已知直线x-y=0与圆x2+y2=8相交，则联立方程组有______________，用代入消元法消去一个未知数得______________，解方程组，其解是______________，所以直线与圆的交点是______________，其弦长是______________.

2.已知直线x-y+1=0与圆x2+y2=5相交，则直线与圆的交点是______________，其弦长是___________.

【题型5】直线与圆相交、相切、相离的条件应用

例1　若直线y=-x+b与圆（x-1）2+y2=2有交点，则b的取值范围是（　）.

A.［-3，-1］　B.［-3，1］　C.［-1，3］　D.［1，3］

解：圆心（1，0）到直线x+y-b=0的距离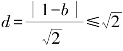，解得-1≤b≤3.

所以答案选　C.

例2　已知圆心为（1，0）的圆经过一点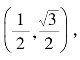（1）求该圆的标准方程；（2）若直线（1+a）x+y+1=0与该圆相切，求a的值.

解：（1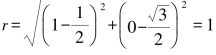），圆的标准方程为（x-1）2+y2=1.

（2）圆心（1，0）到直线（1+a）x+y+1=0的距离

由于直线与圆相切，所以d=r，则

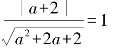解得　a=-1.(www.xing528.com)

【锦囊妙计】直线与圆相交时，常常通过解Rt△来解答问题.

赢在起点

1.已知直线y=x+m，圆x2+y2=3，若直线与圆相离，则b的取值范围是____________；若直线与圆相切，则b的取值范围是________________；若直线与圆相交，则b的取值范围是________________.

2.圆（x-2）2+（y+3）2=2与直线x+y+m=0相切，则m=___________.

一、填空题

1.当圆与直线相交时，d________r；当圆与直线相切时，d________r；当圆与直线相离时，d________r，这里的d表示的是_____________________________.

2.点P（x0，y0）到直线Ax+By+C=0的距离d=____________________________.

3.圆（x-5）2+（y+3）2=20中，其圆心坐标是_____________，半径是____________.　

4.圆（x+2）2+（y-1）2=16的圆心坐标是________，半径r=________，圆心到直线3x+4y-5=0的距离d=________，d________r，圆与直线的位置关系是____________________.

5.圆（x-3）2+（y-1）2=10与直线3x+y=0的位置关系是____________________.

6.圆x2+（y-4）2=5与直线x+2y+7=0的位置关系是____________________.

7.过圆（x-1）2+（y-2）2=4外一点M（5，3）作圆的切线，则切线长为____________.

8.过圆x2+y2=25上一点P（4，3）的切线方程是____________________.

9.过圆（x+1）2+（y-3）2=25上一点Q（2，-1）的圆的切线方程是_____________.

10.圆（x+1）2+（y-3）2=9上一动点M到直线4x-3y-7=0的最短距离是________，最长距离是________.

二、选择题

1.直线2x-y+7=0与圆（x-1）2+（y-1）2=20的位置关系是（　）.

A.相切　B.相离　C.相交且过圆心　D.相交但不过圆心

2.直线2x-y+5=0与圆（x-2）2+y2=1的位置关系是（　）.

A.相切　B.相交　C.相离　D.无法确定

3.若圆与直线有交点，则圆与直线的位置关系正确的是（　）.

A.相交　B.相切　C.相离　D.相交或相切

4.圆（x-2）2+（y-1）2=4与直线3x+4y-10=0的位置关系，下列叙述正确的是（　）.

A.相交且过圆心　B.相切　C.相离　D.相交不过圆心

5.直线x-y-2=0与圆x2+y2=13的交点个数是（　）.

A.2个　B.1个　C.没有交点　D.无法判断

一、填空题

1.圆（x-2）2+（y+3）2=4与直线3x+4y=5的位置关系是________________.

2.圆（x+1）2+y2=5与直线y=2x-3的位置关系是________________.

3.圆x2+y2=36与直线y=3x-20的位置关系是________________.

4.（2013年高考题）已知直线l：x-y+4=0，设M为圆（x-1）2+（y+1）2=8上的一动点，则点M到直线l的最短距离为________________.

5.圆心为C（1，3），并且与直线3x-4y-6=0相切的圆的方程是________________.

6.斜率为3且与圆x2+（y-1）2=10相切的直线方程是________________.

7.圆心在x轴上，半径为2 5，且圆与直线2x-y-4=0相切，则圆的方程为____________.

8.圆x2+y2=10与直线x-y+2=0相交的交点坐标是________________.

9.圆x2+y2=4与直线x-y+2=0相交所截得弦长是________________.

10.过圆外一点P（0，4）向圆（x-2）2+y2=1引切线，则切线长是________________.

二、选择题

1.圆（x+1）2+（y-2）2=2与直线x+y+m=0相切，则m=（　）.

A.±2　B.-3或1　C.1　D.-3

2.圆x2+y2=2与直线x-y+m=0有交点，则m的取值范围是（　）.

A.-2≤m≤2　B.-2＜m＜2　C.m≤-2或m≥2　D.m＜-2或m＞2

3.经过两个定点P（-5，-3）和Q（1，7）作圆，其圆心的轨迹方程是（　）.

A.3x+5y-4=0　B.3x+5y-8=0　C.x-y-2=0　D.x-y+4=0

4.直线3x+4y+7=0与圆（x-3）2+（y+1）2=9的位置关系是（　）.

A.相交　B.相切　C.相离　D.无法判断

三、解答题

1.如图所示，已知圆C的圆心坐标为（4，-2），直线l：2x+y-1=0与该圆相交弦AB的长为4，求圆的方程.

2.若直线y=3x+b与圆（x-1）2+y2=9有公共点，求b的取值范围.

3.已知圆C的方程是x2+y2-2x=0，点M（2，-2），求过点M且与圆C相切的直线方程.

4.圆心为C（3，1）的圆与直线3x+4y+7=0截得的弦长为6，求该圆的方程.

1.求经过点P（1，-2），且与圆x2+y2=4相交，截得弦长为2的直线方程.

2.已知圆C：x2+y2-4x-2y+1=0，直线l：x-my+m-1=0，（1）求证：对m∈R，直线l与圆C相交；（2）直线l与圆相交于A，B两点，若弦AB的长为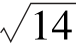，求此时直线l的方程.

3.已知直线l经过点M（0，b），且斜率为1，若直线与圆x2+y2=1有两个公共点，求b的取值范围.

4.已知圆C的方程为：x2+y2+x-6y+3=0，直线l：2x-2y-1=0.

（1）求圆C的圆心坐标和半径；

（2）判断直线l与圆C的位置关系；

（3）若直线x+2y+m=0与圆C相交于A，B两点，试问：是否存在实数m，使得∠AOB=90°（O为坐标原点）？若存在，求出m的值；若不存在，说明理由.

自我评价

（满分100分，时间45分钟）　评价结果：__________

一、填空题（每题5分，共50分）

1.圆（x+3）2+（y-1）2=2的圆心是____________，半径是____________.

2.以点（1，0）为圆心，为半径的圆的标准方程是____________________，且与y轴的交点坐标是____________________.

3.圆心在点C（-2，1），圆过A（1，-1），则圆的方程为____________________.

4.圆x2+y2+2x-4y-4=0的圆心是____________，半径为____________.

5.方程x2+y2+mx+1=0表示圆，则实数m的取值范围是_____________________.

6.圆x2+y2=100的圆心到直线4x-3y=50的距离是____________，直线与圆的位置关系是________________.

7.已知P（2，1）是圆（x+1）2+y2=r2上的一点，那么该圆的半径是________________.

8.经过直线3x+4y-2=0与2x+y+2=0的交点，以C（0，-1）为圆心，则该圆的标准方程是________________.

9.圆心为C（3，-5），与直线x-3y+2=0相切的圆的方程是________________.

10.圆x2+y2-10x-10y=0与圆x2+y2+6x-2y-40=0的圆心距是____________.

二、选择题（每题5分，共20分）

1.方程x2+y2-8x+6y=0表示的曲线是（　）.

A.以（3，-4）为圆心，5为半径的圆　B.以（4，-3）为圆心，25为半径的圆

C.以（4，-3）为圆心，5为半径的圆　D.不表示任何图形

2.直线4x-3y=0与圆（x-3）2+（y+1）2=5的位置关系是（　）.

A.相离　B.相切　C.相交　D.无法确定

3.以点（2，-1）为圆心且与直线3x-4y+5=0相切的圆的方程为（　）.

A.（x-2）2+（y+1）2=3　B.（x+2）2+（y-1）2=3

C.（x-2）2+（y+1）2=9　D.（x+2）2+（y-1）2=9

4.已知圆x2+y2+ax+by-6=0的圆心是（3，4），则半径为（　）.

三、解答题（每题10分，共30分）

1.直线y=x-2与圆x2+y2=9交于A，B两点，求A　B.

2.从圆（x-1）2+（y-1）2=1外一点P（2，3）向这个圆引切线，求切线的方程.

3.一圆的圆心C在x轴上，且此圆经过A（5，-1），已知CA与直线l：2x+y-3=0垂直，求此圆的标准方程.

二次曲线部分

考纲内容：椭圆、双曲线、抛物线的定义、标准方程和几何性质.

考纲要求：理解椭圆的定义、标准方程及其几何性质；了解双曲线、抛物线的定义、标准方程及其几何性质；了解椭圆、双曲线、抛物线的简单应用.