中职数学升学考试教程-求圆的方程

考点剖析：了解曲线方程的概念、理解圆的定义、点在曲线上的条件；掌握圆的标准方程，会求圆的标准方程，会将圆的一般方程转化为标准方程，并会求圆的圆心和半径.

1.圆的定义：平面内与定点距离等于定长的点的轨迹称为圆，定点为圆心，定长为半径.

2.圆的标准方程：设圆心为C（a，b），半径为r，标准方程为（x-a）2+（y-b）2=r2，

特别地，当圆心在坐标原点O（0，0）时，圆的标准方程为x2+y2=r2.

3.圆的一般方程：x2+y2+Dx+Ey+F=0，

配方得

注：（1）当D2+E2-4F＞0，方程表示圆，圆心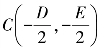，半径

（3）当D2+E2-4F＜0时，方程x2+y2+Dx+Ey+F=0不表示任何图形.

【题型1】根据圆的方程求圆的圆心和半径

例1　圆（x-2）2+（y+3）2=16，则圆心为________，半径为________.

解：圆心为（2，-3），半径为4.

例2　若圆的方程是x2+y2+2x-4y-4=0，则圆心为________，半径为________.

解：x2+2x+1-1+y2-4y+4-4-4=0

（x+1）2+（y-2）2=9

所以圆心为（-1，2），半径为3.

赢在起点

1.圆（x+4）2+（y-2）2=25，则圆心为________，半径为________；圆x2+（y+3）2=1，则圆心为________，半径为________；圆x2+y2=7，则圆心为________，半径为________.

2.圆的方程x2+y2+6x-8y=0，则圆心为________；半径为________.

【题型2】判断形如x2+y2+Dx+Ey+F=0的二元二次方程是否表示圆

例　判断方程x2+y2+4x+6y+17=0表示什么图形.

解：x2+4x+22-4+y2+6y+32-9+17=0

（x+2）2+（y+3）2=-4

因为若表示圆则r2＞0，而-4＜0

所以原方程不表示任何图形.

赢在起点

1.方程x2+y2+4x+6y+10=0表示____________________（图形）.

2.方程x2+y2+4x+6y+14=0表示____________________（图形）.

【题型3】求圆的方程

例1　已知圆心为（-1，2）的圆经过一点（3，4），求该圆的标准方程.

解：r=

圆的标准方程为（x+1）2+（y-2）2=20.

例2　求经过3点A（0，0），B（1，1），C（4，2）的圆的方程.

解：设圆的方程为x2+y2+Dx+Ey+F=0，

则有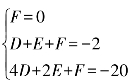

解得　D=-8，E=6，F=0

故所求方程为x2+y2-8x+6y=0.

例3　求经过点A（1，-1），B（3，1），圆心在y轴上的圆的方程.

解：设圆的圆心坐标为C（0，b），半径为r，则圆的标准方程为x2+（y-b）2=r2，

由题意得（1-0）2+（-1-b）2=（3-0）2+（1-b）2

解得b=2，所以圆的圆心C（0，2），

又r2==12+（b+1）2=1+32=10　

则圆的方程为x2+（y-2）2=10.

例4　已知圆的半径为3，圆心在直线x-y=0上，且圆过点（5，2），求圆的方程.

解：由题意设圆的方程为（x-a）2+（y-b）2=9.

因为圆心（a，b）在直线x-y=0上，则a-b=0，

又点（5，2）在圆上，则（5-a）2+（2-b）2=9，

由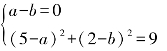

解得

所以圆的方程为（x-2）2+（y-2）2=9或（x-5）2+（y-5）2=9.

【锦囊妙计】求圆的标准方程即是求圆心和半径.

赢在起点

1.圆心为（3，-5），半径为5的圆的标准方程是__________.

2.以C（2，-4）为圆心的圆经过M（3，-2），则圆的方程是__________.

3.已知A（3，-1），B（-1，7），则以AB为直径的圆的方程是________.

【题型4】解决与圆有关的简单问题

例1　若方程x2+y2-2x+ay+2=0表示圆，求a的取值范围.

解：x2+y2-2x+ay+2=0

若方程表示圆，则

解得｛＞2或a＜-2｝.

例2　已知关于x，y的二元二次方程x2+y2-2mx+4my+20=0，（1）若此方程表示一个圆，求实数m的取值范围；（2）当此方程所表示的圆的圆心C的坐标为（-3，6），求该圆的标准方程.

解：（1）由x2+y2-2mx+4my+20=0得

（x-m）2+（y+2m）2=5m2-20

若此方程表示圆，则5m2-20＞0

解得m＜-2或m＞2.

所以m的取值范围是｛＜-2或m＞2｝.

（2）若（x-m）2+（y+2m）2=5m2-20表示圆，则

圆的圆心坐标为（m，-2m），半径为

又圆的圆心C（-3，6）(https://www.xing528.com)

则有m=-3且-2m=6，解得m=-3，

r==5

所以圆的标准方程为（x+3）2+（y-6）2=25.

赢在起点

1.若方程x2+y2-6x+4y+m=0表示圆，m的取值范围是_________________.

2.若方程x2+y2+ax-2y+5=0表示圆，a的取值范围是________________.

3.圆（x-a）2+（y-b）2=4a-b的圆心是（1，2），则该圆的半径是________.

一、填空题

1.（1）圆的标准方程是________________________，圆心坐标是____________________，半径是____________.

（2）圆的一般方程是________________________.

2.以C（-2，4）为圆心，半径为3的圆的标准方程是____________________；以点（3，-2）为圆心，5为半径的圆的标准方程是______________；以原点为圆心，4为半径的圆的标准方程是_________________.

3.圆（x+2）2+（y-5）2=16的圆心坐标是____________，半径是____________；圆x2+y2=9的圆心坐标是____________，半径是____________.

4.（1）圆x2+y2-2x+6y-15=0化为标准方程是____________________；

（2）圆x2+y2+4x-8y+11=0化为标准方程是____________________.

5.方程x2+y2-4x-6y-12=0表示的图形是________，如果是圆，其圆心坐标是____________，半径是____________.

6.以点C（-2，5）为圆心，经过原点的圆的标准方程是________________.

7.以点C（1，2）为圆心，经过点A（3，5）的圆的方程是________________.

8.点M（m，2）在曲线x2+y2-2y-1=0上，则m=____________.

9.方程x2+y2+6x-2y+10=0是____________________（图形）.

10.方程x2+y2-8x+2y+19=0是____________________（图形）.

二、选择题

1.已知圆的方程为（x+1）2+（y-2）2=9，则它的圆心坐标和半径分别为（　）.

A.（1，-2），3　B.（-1，2），3　C.（1，-2），9　D.（-1，2），9

2.已知（x-3）2+（y+1）2=4，则圆心坐标和半径分别为（　）.

A.（-3，1），2　B.（3，-1），2　C.（-3，1），4　D.（3，-1），4

3.方程x2+y2+6x-8y-11=0表示的曲线是（　）.

A.以（3，-4）为圆心，6为半径的圆　B.以（-3，4）为圆心，6为半径的圆

C.以（-3，4）为圆心，36为半径的圆　D.不表示任何图形

4.已知A（1，3），B（-1，1），则以线段AB为直径的圆的方程是（　）.

A.（x+1）2+（y-1）2=2 　B.x2+（y-2）2=2

C.x2+（y-4）2=2　D.x2+（y-2）2=8

5.已知圆的方程为（x-3）2+（y-5）2=16，则点（2，-1）（　）.

A.在圆内不与圆心重合　B.在圆上

C.在圆外　D.与圆心重合

一、填空题

1.已知A（1，-4），B（-3，4），则以AB为直径的圆的方程是________________.

2.以点C（1，3）为圆心，与x轴相切的圆的标准方程是________________.

3.圆（x+1）2+（y-4）2=25与x轴的交点坐标是________________.

4.倾斜角为45°，且经过圆（x-1）2+（y+2）2=7的圆心的直线方程是________________.

5.经过圆（x-2）2+（y+3）2=9的圆心，且与直线y=-2x+7垂直的直线是________________.

6.经过（x-4）2+（y-2）2=16的圆心且与直线y=-2x+5平行的直线方程是________________.

7.方程x2+y2+λx+1=0表示圆，则实数λ的取值范围是_________________.

8.以C（2，1）为圆心并且经过直线2x+y+7=0与x-2y-4=0的交点的圆的方程是________________.

9.圆（x-3）2+（y+1）2=49的圆心到直线3x-4y+7=0的距离是________________.

10.圆C1：x2+（y-1）2=16与圆C2：（x+1）2+（y-2）2=25的圆心距是________________.

二、选择题

1.设线段PQ是以点C（1，1）为圆心的圆的一条直径，已知点P的坐标为（3，-1），则点Q的

坐标为（　）.

A.（-2，2）　B.（2，0）　C.（-1，2）　D.（-1，3）

2.圆x2+y2+4x=1的圆心坐标及半径分别是（　）.

A.（-2，0），5　B.（2，0），5　C.（-2，0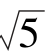），　D.（2，0），

3.已知圆C1：x2+y2+2x+6y+6=0和圆C2：x2+y2-8x-4y+7=0，则圆心距为（　）.

A.5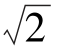　B.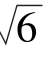　C.5　D.2+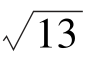

4.已知圆x2+y2+mx+ny-6=0的圆心是（-1，3），则圆的半径为（　）.

A.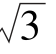　B.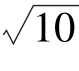　C.4　D.5

5.以抛物线y2=-16x的焦点为圆心，焦点到准线的距离为半径的圆的方程是（　）.

A.（x+4）2+y2=16　B.（x-4）2+y2=16

C.（x+4）2+y2=64　D.（x-4）2+y2=64

三、解答题

1.设圆的半径为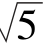，且圆过A（3，1）和B（-1，1），求该圆的标准方程.

2.已知某圆经过（0，0），（2，0），（1，1）3点，（1）求该圆的方程；（2）求该圆的圆心和半径.

3.求以椭圆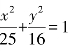的焦距为直径的圆的方程.

1.求过点A（6，0）和B（1，5）且圆心在直线2x-7y+8=0上的圆的方程.

2.求以直线3x-y+2=0和直线x+2y-11=0交点为圆心，半径为3的圆的方程.

3.求直线x-y-2=0被抛物线y2=2x截得的线段为直径的圆的方程.