两条直线的位置关系-中职数学升学考试教程

考点剖析：理解并识记两条直线的位置关系的充要条件、两点间的距离公式、中点坐标公式和点到直线的距离公式；会求两点间的距离、点到直线的距离、两直线的交点坐标，会利用两直线平行、重合、垂直的充要条件解决相关的几何问题.

1.两条直线的位置关系

2.中点坐标公式

若A（x1，y1），B（x2，y2），则A，B中点C的坐标为

3.两点间的距离公式

若A（x1，y1），B（x2，y2），则A，B两点间的距离为

4.点到直线的距离公式

点P（x0，y0）到直线Ax+By+C=0的距离为

【题型1】判断两条直线的位置关系

例　试判断下列两条直线的位置关系.

（1）直线2x+3y+1=0与直线2x-3y+1=0的位置关系是________________；

（2）直线2x+3y+1=0与直线3x-2y+1=0的位置关系是________________；

（3）直线2x+3y+1=0与直线4x+6y+5=0的位置关系是________________；

（4）直线y=3x-2与直线的位置关系是________________；

（5）直线与直线的位置关系是_________________.

解：相交；垂直；平行；相交；垂直.

赢在起点

1.已知直线y=k1x+b1与直线y=k2x+b2，若平行，则________；若垂直，则____________.

2.已知直线A1x+B1y+C1=0与直线A2x+B2y+C2=0，若平行，则________；若垂直，则____________.

3.直线3x-2y+1=0与直线3x-2y+3=0____________；直线3x-2y+1=0与直线3x+2y-3=0____________；直线3x-2y+1=0与直线2x-3y+2=0____________；直线3x-2y+1=0与直线2x+3y+3=0________.

【题型2】根据两条直线的位置关系解决相关问题

例　已知两条直线l1：4x+（3+m）y+3m-5=0，l2：（5+m）x+2y-8=0，当m为何值时，l1∥l2；当m为何值时，l1⊥l2.

解：因为l1∥l2，所以有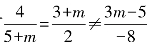，解得m=-7或m=-1（舍去）

所以当m=-7时，l1∥l2；

因为l1⊥l2，所以有4·（5+m）+（3+m）·2=0，解得

所以当时，l1⊥l2.

赢在起点

若直线x-2y+3=0与直线2x+my-5=0平行，则m=____________；若直线x-2y+3=0与直线2x+my-5=0垂直，则m=________.

【题型3】求经过一点与已知直线平行（或垂直）的直线方程

例　求经过点P（-2，3）且与直线l：3x-y+5=0垂直的直线m的方程.

解法1：直线l：3x-y+5=0

y=3x+5

所以kl=3，

因为l⊥m，所以

直线m的方程为

即x+3y-7=0.

解法2：因为l⊥m，所以m的直线可设为x+3y+C=0，

又因为过点P（-2，3），所以-2+3×3+C=0，

解得C=-7，

所以直线m的方程为x+3y-7=0.

【锦囊妙计】凡是与斜率有关的直线方程问题均可用点斜式或斜截式来求解.

赢在起点

1.与直线3x-2y+3=0平行的直线可设为____________；与直线3x-2y+3=0垂直的直线可设为____________.

2.经过点P（-2，3）且与直线l：3x-y+5=0平行的直线n的方程是________.

3.经过点P（2，-1）且与直线l：2x-y+5=0垂直的直线m的方程是________.

【题型4】求两直线的交点坐标

例　求直线3x+y+5=0与直线2x-y+10=0的交点坐标.

解：由题意得

所以两直线的交点坐标是P（-3，4）.

赢在起点

直线x+2y+3=0与直线x-y-6=0的交点坐标是________.

【题型5】与中点有关的问题

例　已知线段MN的中点P的坐标为（4，5），点M的坐标为（-2，1），求点N的坐标.

解：设N（a，b），则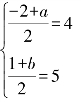

解得a=10，b=9

所以点N的坐标是（10，9）.

赢在起点

1.若M（1，-1），N（3，-5），则MN的中点坐标是____________.

2.若PQ的中点是A（-1，2），Q（3，1），则点P的坐标是____________.

3.点A（3，-2）关于点B（-1，1）对称的点是C，则C的坐标是________.

【题型6】与距离有关的问题

例　（1）已知M（2，-1）、N（3，-4），求

（2）求点P（1，-3）到直线3x-4y+7=0的距离.

（3）求平行直线2x+3y-2=0与2x+3y+11=0之间的距离.

解：（1）因为M（2，-1），N（3，-4），所以

（2）由点到直线的距离公式得

（3）在2x+3y-2=0上取一点P（1，0），点P（1，0）到直线2x+3y+11=0的距离就是这两条平行直线之间的距离，所以

赢在起点

1.已知A（-1，2），B（3，4），则AB的中点C的坐标是______________；AB的距离是____________；AB的斜率是____________；AB的方程是________________.

2.原点到直线2x-y+5=0的距离是________________.

3.平行直线4x-3y-8=0与4x-3y+12=0之间的距离是________.

【题型7】点、直线、距离的简单应用

例1　求斜率为2，原点到它的距离是3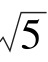的直线方程.

解：设所求直线方程为：y=2x+b

2x-y+b=0

则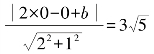

化简得

b=±15

所以直线的方程为：2x-y+15=0或2x-y-15=0.

例2　x轴上一点A（a，0）到直线3x-4y+7=0的距离不小于2，求a的取值范围.

解：由题意得d≤2，则有

解得≤a≤1

所以a的取值范围是

赢在起点

1.已知直线l在y轴上的截距为3，且点A（1，1）到直线l的距离为1，则直线的方程是____________________.

2.已知直线l在x轴上的一点A与B（-2，3）的距离不小于5，则点A的坐标是________.(www.xing528.com)

一、填空题

1.（1）直线5x+3y-1=0与直线10x+6y+8=0的位置关系是____________.

（2）直线5x+3y-1=0与直线10x+6y-2=0的位置关系是____________.

（3）直线5x+3y-1=0与直线5x-3y-1=0的位置关系是____________.

（4）直线5x+3y-1=0与直线3x-5y+7=0的位置关系是____________.

（5）直线y=2x+3与直线y=2x-5的位置关系是________________.

（6）直线y=2x+3与直线y=-2x+5的位置关系是________________.

（7）直线y=2x+3与直线y=-x+5的位置关系是________________.

2.（1）直线l的方程是y=-4x-2，m∥l，则直线m的斜率为________________.

（2）直线l的方程是y=-4x-2，m⊥l，则直线m的斜率为________________.

3.（1）若直线2x+y-1=0与ax-2y-3=0垂直，则a=________________.

（2）若直线2x+y-1=0与ax-2y-3=0平行，则a=________________.

4.直线x+2y-3=0与直线3x-y-2=0的交点坐标是____________.

5.已知A（2，0），B（-1，3），则AB的中点C的坐标是_____________；A，B两点间的距离是_____________.

6.（1）点M（-2，3）到直线x-y+1=0的距离是________________.

（2）点P（-3，1）到直线3x+4y+10=0的距离是________________.

7.点P（3，0）到直线y=x+9的距离是______________.

8.平行直线x-2y+1=0与x-2y-4=0之间的距离是________________.

二、选择题

1.点P（2，1）到直线l：3x+4y+5=0的距离是（　）.

A.1　B.2　C.3　D.4

2.（2013年高考题）过点P（1，0），且与直线x-2y-2=0平行的直线方程是（　）.

A.x-2y-1=0　B.x-2y+1=0　C.x+2y-1=0　D.2x+y-2=0

3.直线x+2y+3=0与直线2x+my-5=0垂直，则m的值为（　）.

A.2　B.1　C.　D.-1

4.过点P（0，-1），且垂直于直线2x-5y+3=0的直线方程是（　）.

A.2x-5y+5=0　B.2x-5y-5=0　C.5x+2y+2=0　D.5x-2y-2=0

5.两条直线l1：3x-4y+5=0与l2：3x-4y-5=0的位置关系是（　）.

A.重合　B.平行　C.垂直　D.相交但不垂直

一、填空题

1.经过点（1，3）且与直线x-2y+4=0垂直的直线方程为________________.

2.经过点（1，3）且与直线x-2y+4=0平行的直线方程为________________.

3.已知直线3x-y+2=0与直线x+ay+1=0垂直，则a=____________.

4.两条平行直线3x+4y-4=0与6x+8y+12=0的距离为____________.

5.已知直线3x-y+6=0与直线ax+y-3=0平行，则a=____________.

6.（2013年高考题）坐标原点到直线3x-4y+8=0的距离为________________.

7.x轴上一点P与点A（12，-5）之间的距离为13，则P点的坐标是________________.

8.若点A（2，m）到直线3x-4y-2=0的距离为4，则m=____________.

9.若直线3x+（1-n）y+5=0与直线y=x平行，则n=____________.

10.△ABC的3个顶点的坐标分别为A（0，5），B（1，-3），C（-5，4），AB边上的高所在的直线方程为________________.

二、选择题

1.直线kx+4y+3=0，与直线x-2y-5=0没有公共点，则k=（　）.

A.-2　B.2　C.　D.8

2.若A（3，-2），B（5，-4），则线段AB的垂直平分线的方程为（　）.

A.x-y-7=0　B.x-y+7=0　C.2x-y-11=0　D.x+2y+2=0

3.原点到直线y=kx+2的距离是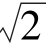，则k=（　）.

A.±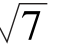　B.±1　C.1　D.-1

4.（2013年高考题）点P（4，2）关于直线l：x-y=0的对称点的坐标为（　）.

A.（-4，-2）　B.（-4，2）　C.（2，-4）　D.（2，4）

5.已知过点P（-1，n），Q（n，5）的直线l1与直线l2：x+y=0垂直于点M，则点M的坐标为（　）.

三、解答题

1.已知直线l经过点A（-2，1），B（1，3），（1）求直线l的斜率；（2）求直线l的方程.

2.已知直线l1：x-y+1=0和l2：2x+y+2=0相交于点P，（1）求点P的坐标；（2）求经过点P且与直线3x-4y+5=0平行的直线方程.

3.已知直线x-y-3=0和2x+my+1=0相交于点A，且A到直线x+y+1=0的距离为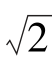，求m.

1.已知直线l与直线2x-y+1=0平行，且l与原点的距离是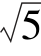，求l的方程.

2.设点A（a，5）到直线4x-3y=2的距离为d，若d＜2，则a的取值范围.

3.已知直线l与直线3x+2y+5=0垂直，且l与点P（1，1）的距离为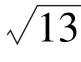，求直线l的方程.

4.若直线l与直线x-y+1=0垂直，且与两坐标轴围成的三角形的面积是4，求直线l的方程.

自我评价

（满分100分，时间45分钟）　评价结果：__________

一、填空题（每题5分，共50分）

1.已知点M（3，a）在直线l：2x-y+1=0上，则a=____________.

2.已知直线斜率的绝对值等于1，则直线的倾斜角是____________.

3.经过点A（4，-2），且倾斜角是120°的直线的斜率k=____________，直线方程为____________________.

4.已知直线方程为y=2x-1，则直线的斜率k=________，直线在y轴上的截距b=________.

5.若直线l过（-2，3）和（6，-5）两点，则直线l的斜率为________，倾斜角为________.

6.过点（4，2），平行于x轴的直线方程为____________；过点（-2，0），垂直于x轴的直线方程为____________.

7.垂直于直线2x+y-5=0，且过点（3，0）的直线方程为________________.

8.两条直线3x+y-4=0与x-2y+1=0的交点坐标为________________.

9.点（1，-2）到直线3x-4y+2=0的距离是________________.

10.当m=_____________时，经过两点P（-m，6），Q（1，3m）的直线的斜率是12.

二、选择题（每题5分，共20分）

1.已知点A（2，-1），B（-4，3），则直线AB的斜率是（　）.

2.过点P（-1，3），且平行于直线x-2y+5=0的直线l的方程为（　）.

A.2x-y+7=0　B.2x+y-1=0　C.x-2y+7=0　D.x-2y-7=0

3.直线3x-4y+2=0与直线4x+3y-1=0的位置关系是（　）.

A.垂直　B.平行　C.相交但不垂直　D.重合

4.经过两点（-1，1），（3，9）的直线在x轴上的截距是（　）.

三、解答题（每题10分，共30分）

1.在y轴上有一点P，它与点A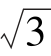（-，1）连成一条直线，直线的倾斜角为120°，求点P的坐标.

2.已知点P（1，2），Q（3，1），求线段PQ的垂直平分线l的方程.

3.求经过直线2x-3y+7=0与3x+y-6=0的交点，且与直线x+2y-3=0平行的直线方程.

圆部分

考纲内容：圆的方程、圆与直线的位置关系.

考纲要求：掌握圆的一般方程和标准方程；会将圆的一般方程转化为标准方程；理解圆与直线相交、相切、相离的条件.