中职数学升学考试教程：直线方程及其计算方法

考点剖析：了解直线方程的一般式，理解直线的倾斜角、斜率、直线在坐标轴上的截距概念；会求直线的斜率，熟练掌握用点斜式、斜截式求直线方程，并能把方程化成一般方程.

1.直线的倾斜角：一条直线向上的方向与x轴的正方向所形成的最小正角，它的取值范围是［0°，180°）.

2.斜率.

（1）直线的倾斜角的正切值称为斜率：

k=tan α（α≠90°）

（2）如果一条直线经过两点A（x1，y1），B（x2，y2），则直线的斜率：

当直线的倾斜角α=90°时，直线垂直于x轴，直线的斜率不存在；当直线的倾斜角α=0°时，直线平行于x轴，直线的斜率为0.

3.直线的截距：在平面直角坐标系中，直线与y（或x）轴的交点的纵（或横）坐标称为直线在y（或x）轴上的截距.

直线的截距可正、可负、也可为零.

4.直线方程的几种常见形式：

（1）两点式（了解）：一条直线经过两点A（x1，y1），B（x2，y2），则直线方程为

当x1=x2时，直线方程为x-x1=0；当y1=y2时，直线方程为y-y1=0.

（2）点斜式：一条直线经过点P（x0，y0），且它的斜率为k，则直线方程为

y-y0=k（x-x0）

（3）斜截式：一条直线的斜率为k，且它在y轴上的截距为b，则直线方程为

y=kx+b

（4）截距式（了解）*：一条直线在x轴上的截距为a，在y轴上的截距为b，则直线方程为

（5）一般式：Ax+By+C=0（A、B不同时为0）

5.几种特殊的直线方程：

（1）经过点P（a，b）平行于x轴的直线，其方程为y=b；经过点P（a，b）垂直于x轴的直线，其方程为x=a.

（2）x轴所在的直线方程为y=0；y轴所在的直线方程为x=0.

（3）一、三象限角平分线的直线方程为y=x；二、四象限角平分线的直线方程为y=-x.

【题型1】求直线的斜率和截距

例1　已知直线l的倾斜角为45°，则直线l的斜率是________；直线m经过A（-2，5），B（3，7），则直线m的斜率是____________.

解：k=tan 45°=1；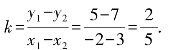

例2　已知直线l的方程为3x+2y-6=0，则直线l的斜率是________；y轴上的截距是________.

解：由3x+2y-6=0变形得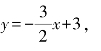

所以直线的斜率，y轴上的截距是3.

赢在起点

1.已知直线l的倾斜角为135°，则直线l的斜率为________.

2.直线m经过A（3，-1），B（4，2），则直线m的斜率是________.

3.直线3x-2y-12=0，则该直线m的斜率是________；它在x轴上的截距是________；它在y轴上的截距是________.

4.直线l：y=3x-2，直线l的斜率是________；若直线m的斜率是直线l的斜率的负倒数，则直线m的斜率是__________；若直线m的斜率是直线l的斜率的2倍，则直线m的斜率是________；若直线m的倾斜角是直线l的倾斜角的2倍，则直线m的斜率是________.

【题型2】求直线的方程

例1　已知直线l经过点P（-2，3），其倾斜角为135°，求直线的方程并把它化为一般式.

解：因为直线的倾斜角为135°，所以k=tan 135°=-1，

由直线方程的点斜式表示为y-3=-1［x-（-2）］，

化简得y=-x+1，

化为一般式为x+y-1=0.

例2　已知一条直线过点P（2，3）且其倾斜角比直线x-2y-3=0的倾斜角大45°，求这条直线的方程.

解：由x-2y-3=0，得

直线的斜率为，设它的倾斜角为α1，则

又设所求直线的倾斜角为α2，则k2=tan α2=tan（α1+45°），

所求直线方程为y-3=3（x-2）.

即　3x-y-3=0.

赢在起点

1.已知斜率为3的直线l经过点A（2，-1），则直线的方程是________________.

2.直线m经过A（3，-1），B（4，2），则直线m的斜率是________________，其方程是________________.

3.斜率为5的直线m在y轴上的截距为4，则直线m的方程是________.

【题型3】利用直线方程解决与面积（或周长）有关的几何问题

例1　已知直线l的方程为3x-4y+12=0，（1）求直线的斜率；（2）求直线与坐标轴围成的三角形的面积.

解：（1）3x-4y+12=0

4y=3x+12

y=

所以直线的斜率是

（2）令x=0，则y=3，直线过点A（0，3）（如图所示）

又令y=0，则x=-4，直线过点B（-4，0）

所以

例2　已知直线x+y-2=0和x+my+1=0与x轴围成的三角形的面积为，则求m的值.

解：在x+y-2=0中，设y=0，解得x=2，所以它与x轴交于A（2，0），

在x+my+1=0中，设y=0，解得x=-1，所以l2与x轴交于B（-1，0），(www.xing528.com)

又由解得l1与l2的交点C的纵坐标为

由列方程，

解之得，m=4或m=-2.

赢在起点

1.直线l：5x+y-15=0与两坐标轴围成的三角形的周长是____________，其面积是____________.

2.已知直线l1：x+2y-5=0，l2：2x+y+2=0，则直线l1与直线l2及x轴所围成的三角形的面积是________.

一、填空题

1.若点A（1，m）在直线x+2y-5=0上，则m=_________________.

2.直线倾斜角α的范围是____________；当时，斜率k____________0；当时，斜率k__________0；当α=0时，斜率k__________0；当时，斜率k____________.

3.（1）若直线的倾斜角为60°，则它的斜率是____________.

（2）若直线的倾斜角为，则它的斜率是____________.

（3）若直线的倾斜角为120°，则它的斜率是____________.

（4）若直线的斜率为-1，则它的倾斜角是____________.

（5）若直线过点P（2，-1），Q（-3，2），则直线的斜率是____________.

4.若直线过点M（1，-4）且斜率为3，则直线方程是____________.

5.若直线过点P（1，2），Q（3，-1），则直线方程是____________.

6.若直线的斜率为5，它在y轴上的截距为2，则直线方程是____________.

7.若直线方程3x-2y-12=0，则它在x轴上的截距是____________；y轴上的截距是____________.它与两坐标轴围成的三角形面积是____________.

8.若直线方程x+2y-7=0，则它的斜率是________________.

9.若直线过点P（3，-4）且平行于x轴，则直线方程是________，它的斜率是________.

10.若直线过点P（3，-4）且垂直于x轴，则直线方程是________，它的斜率是________.

二、选择题

1.已知△ABC的3个顶点坐标分别为A（4，-2），B（3，1），C（2，5），那么AC边所在直线的斜率是（　）.

2.已知△ABC的3个顶点坐标分别为A（4，-2），B（3，1），C（2，5），那么AB边所在直线的方程是（　）.

A.3x+y-10=0　B.3x-y-8=0　C.x-3y+10=0　D.x+y-7=0

3.直线3x+y-2=0的斜率是（　）.

A.2　B.3　C.　D.-3

4.斜率为4，且经过P（1，7）的直线方程是（　）.

A.4x-y+7=0　B.x-4y-3=0　C.4x-y+3=0　D.4x+y-7=0

5.直线x-2y-3=0的斜率和在y轴上的截距正确的是（　）.

一、填空题

1.若点A（1，2）在直线ax+2y+3=0上，则a=________________.

2.若点B（m，3）不在直线2x-y+7=0上，则m的取值范围是________________.

3.若直线过点M（2，3），且它的倾斜角是45°，则该直线方程是________________.

4.若直线l在x轴和y轴上的截距分别为2和-3，则该直线方程是________________.

5.若直线的斜率为5，它在x轴上的截距为-2，则直线方程是________________.

6.直线l：4x-3y+12=0与两坐标围成的三角形的周长是________________，与两坐标轴围成的三角形面积是________________.

7.直线l的斜率为3，直线m的斜率是它的2倍，且直线m在y轴上的截距为5，则直线m的方程是________________.

8.若直线l经过点M（1，3），且它的斜率是2的负倒数，则直线l的方程是________________.

9.若斜率为-3的直线经过抛物线y2=4x的焦点，则它的方程是________________.

10.若斜率为4的直线l经过椭圆的左焦点，则直线l的方程是________________.

二、选择题

1.斜率为3的直线经过圆（x-2）2+（y+5）2=16的圆心，则该直线方程是（　）.

A.3x-y-11=0　B.3x-y-1=0　C.x+y-5=0　D.3x+y-11=0

2.直线l经过P（3，2），Q（-1，m）两点，且它的斜率为5，那么m=（　）.

A.5　B.-18　C.-4　D.6

3.若直线l经过A（m，-1），B（2，5），C（4，n）3点，其斜率为3，则m，n的值分别是（　）.

A.0，11　B.0，10　C.11，0　D.6，11

4.已知直线l：3x-y+1=0，直线m经过点M（3，2），m与l的斜率相同，则直线m的方程正确的是（　）.

A.3x+y+5=0　B.x-3y+5=0　C.4x+y+1=0　D.3x-y-7=0

5.已知直线l：2x+y+1=0，直线m的斜率与直线l的斜率互为相反数，且直线m经过双曲线的右焦点，则直线m的方程是（　）.

A.2x+y+10=0　B.x-2y-5=0　C.2x-y-5=0　D.2x-y-10=0

三、解答题

1.已知直线l的方程为3x-y+9=0，求：（1）该直线的斜率；（2）它与两坐标轴的交点坐标.

2.已知直线的斜率为5，它经过点M（-3，-4），求：（1）直线的方程；（2）直线与两坐标轴围成的三角形的面积.

3.△ABC的3个顶点的坐标分别为A（-1，5），B（1，-3），C（-5，4），求AB边上的中线所在直线的方程.

1.已知直线过点P（2，1），直线和两坐标轴的正半轴交于A，B两点，当△AOB的面积为4时，求此直线的方程.

2.已知直线经过M（3，2），且它在y轴上的截距是4，求该直线的方程.

3.已知直线l：3x+y+1=0，直线m的倾斜角比直线l的倾斜角小45°，且它经过点M（-1，4），求直线m的方程.