等比数列的首项、公比、通项公式和前n项和

考点剖析：理解等比数列的概念；识记等比数列的通项公式、等比中项、前n项和的公式；会求等比数列的通项公式、等比中项、前n项和；能用等比数列知识解决有关简单实际问题.

1.等比数列的定义

（1）定义：如果一个数列，从第二项起，每一项与它的前一项之比都为同一个不为0的常数，那么这个数列就称为等比数列.这个常数称为公比，通常用q来表示.

（2）定义表达式：即

注：①常用此定义来判断或证明一个数列是否是等比数列；

②一个数列为等比数列的必要条件是该数列各项均不为零.

2.通项公式：等比数列{an}的首项为a1，公比q，则通项公式：

an=a1qn-1（q=1时，an是一个常数列）.

推导：　an=amqn-m（n，m∈Z+，且n≥m）.

3.等比中项：若a，b，c 3个数成等比数列⇔b称为a与c的等比中项，则有

4.前n项和公式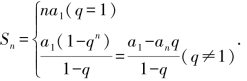

5.性质：设{an}为等比数列，p，q，m，n为正整数.

当p+q=m+n时，有apaq=aman.

特别地：当m=n时，上结论仍成立.

【锦囊妙计】3个数成等比数列时，通常设这3个数为：，a，a·aq.

【题型1】等比数列的定义及其通项公式

例　下列数列哪些是等比数列，如果是，其公比是多少？

（1）2，-4，8，-16，32，-64；

（2）2，6，18，54，162；

（3）5，5，5，5，5；

（4）3，-3，3，-3，3；

（5）1，2，-4，8，16；

（6）25，5，1，

解：（1）是，公比q=-2；（2）是，公比q=5；（3）是，公比q=1；（4）是，公比q=-1；（5）不是；（6）是，公比q=

赢在起点

1.（1）在等比数列｛an｝中，a1=8，公比q=2，则a2=________，a3=________，a4=________，其通项公式是________________；

（2）在等比数列｛an｝中，a1=8，公比，则a2=________，a3=________，a4=________，其通项公式是____________________；

（3）在等比数列｛an｝中，a1=3，公比q=2，则a2=________，a3=________，a4=________，其通项公式是_____________________.

2.（1）在等比数列｛an｝中，a3=125，公比q=5，则a2=________，a1=________，a4=________；

（2）在等比数列｛an｝中，a6=27，公比q=-3，则a3=________，a1=________，a7=________.

3.（1）在等比数列｛an｝中，当公比q=1时，这个数列也是_________________数列；

（2）在等差数列｛an｝中，因为公比q≠0，所以其任一项的值都不会__________0.

【题型2】根据等比数列中的已知量，求其他未知量

例1　在等比数列{an}中，Sn是它的前n项和，a2=2，S3=7，求公比q的值.

解：由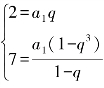解得或2

例2　在等比数列{bn}中，b5+b6=48，b7-b5=48，求bn和S10.

解：由已知得

代①入②得q-1=1，所以q=2，

将q=2代入公式①得b1=1，

bn=b1qn-1=1×2n-1=2n-1，

即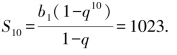　

赢在起点

1.在等比数列｛an｝中，a2=2，a3=-4，则a5=____________.

2.在等比数列｛an｝中，a1+a4=18，a2+a3=12，则这个数列的公比是____________.

3.在等比数列｛an｝中，a3=9，9a2+a4=54，则a1=________，q=________，an=________，Sn=__________.

【题型3】等比数列性质的应用

例1　在等比数列{an}中，已知a7·a12=5，则a8·a9·a10·a11=（　）.

A.10　B.50　C.25　D.75

解：a8·a9·a10·a11=（a8·a11）2=（a7·a12）2=25，选　C.

例2　等比数列{an}中，a4=4，则a2·a6等于（　）.

A.4　B.8　C.16　D.32

解：由题根据等比数列中项的性质可得a2·a6=a42=16，故选　C.

例3　各项为正的等比数列{an}中，若a5a6=9，求log3a1+log3a2+…+log3a10的值.

解：因为a1a2…a10=（a1a10）（a2a9）…（a5a6）=95

所以log3a1+log3a2+…+log3a10

=log3（a1a2…a10）=log395=5 log39=10.

赢在起点

1.等比数列{an}中，a2=4，a4=8，则a6=______________；

2.等比数列{an}中，a2=4，a6=16，则a4=______________；(www.xing528.com)

3.等比数列{an}中，a1=4，a7=16，则a4=______________；

4.两数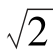+1与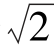-1的等比中项是__________.

一、填空题

1.已知等比数列中，a2=2，a4=8，则公比q=________________.

2.等比数列2，-4，8，-16，…的公比q=____________，它的首项a1=____________，通项公式an=________________，它的第8项为____________，前n项和Sn=____________，前10项的和为____________.

3.等比数列{an}中，a1=9，公比q=2，则an=____________，a4=_____________.

4.数列-1，2，-4，8，…的通项公式an=____________，前n项和Sn=____________，前10项和S10=____________.

5.在等比数列{an}中，a4=2，a8=32，那么a6=________，则公比q=___________.

6.在等比数列{an}中，a5=2，a7=32，那么a6=________，则公比q=__________.

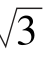7.7+3和7-3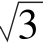的等比中项是____________.

8.已知等比数列{an}中，a1a7=10，则a2a6=____________，a4=__________.

9.已知等比数列{an}中，a4=4，则a2·a6=____________.

10.已知等比数列{an}中，若公比q=4，且前3项之和等于21，则该数列的通项公式an=________.

二、选择题

1.下列数列是等比数列的是（　）.

A.1，2，4，8　B.-4，6，8　C.1，2，3，4　D.0，0，0，0

2.设5，x+1，5成等比数列，则x=（　）.

A.4或-4　B.-4，6　C.4或-6　D.4或6

3.“b2=ac”是“a，b，c成等比数列”的（　）.

A.充分条件　B.必要条件　C.充要条件　D.非充分非必要条件

4.已知等比数列的公比q为2，若前4项之和为1，那么前8项之和为（　）.

A.15　B.17　C.19　D.21

5.已知某等比数列的前3项为1，-2，4，则它的第4项为（　）.

A.-8　B.-6　C.6　D.8

一、填空题

1.某厂2002年的产值为a万元，预计产值每年增长5%，则该厂到2010年产值为________万元.

2.某种细菌在分裂过程中，每10分钟分裂一次（1个分为2个）经过1个半小时，这种细菌由1个变成了________个.

3.设{an}是等比数列，已知a9·a11·a16=64，则a12=________.

4.已知2，x，y，z，32成等比数列，则3个数分别为____________.

5.数列1，-3，9，-27，81，…的一个通项公式为____________.

6.等比数列{an}中，在Sn是它的前n项和，其中a3=4，S3=7，那么公式q=__________.

7.在等比数列{an}中，已知a7·a12=5，则a8·a9·a10·a11=____________.

8.等比数列{an}中，已知a2和a10是方程x2+3x+2=0的根，那么a6=____________.

9.已知2x，2，2x2依次组成等比数列，那么实数x=____________.

10.已知3个数依次组成等比数列，则x的值为____________.

二、选择题

1.数列1，-2，4，-8，16，…的一个通项公式为（　）.

A.an=（-1）n+1·2n（n∈N*）　B.an=（-1）n+1·2n-1（n∈N*）

C.an=（-1）n·2n（n∈N*）　D.an=（-1）n·2n-1（n∈N*）

2.在等比数列{an}中，若a4=8，q=-2，则a7的值为（　）.

A.-64　B.64　C.-48　D.48

3.在等比数列{an}中，Sn是它的前n项和，a2=2，S3=7，那么公比q=（　）.

4.等差数列{an}中公差为2，若a1，a3，a4成等比数列，则a2=（　）.

A.-6　B.-8　C.8　D.6

5.（2002年高考题）某种细菌在培养过程中，每20分钟分裂一次，每次分裂的规律是每个

细菌分裂为2个细菌.那么，经过2小时这种细菌由1个分裂成（　）.

A.63个　B.64个　C.31个　D.32个

三、解答题

1.在等比数列{an}中，a3=12，a4=24，求a5.

2.已知3个数成等比数列，其和为26，其积为-512，求这3个数.

3.在等比数列{an}中，a2=2，a5=16，求前6项的和S6.

4.（2016高考题）在等比数列{an}中，，a4=-16，（1）求公比q；（2）求数列{}的前n项和Sn.

1.在等比数列{an}中，S5=242，q=3，求a1和a5.

2.3个数a，b，c成等差数列，公差为3，a，b+1，c+6成等比数列，求a，b，c的值.

3.有4个整数，其中前3个数成等差数列，后3个数成等比数列，并且第一个数与第4个数之和为37，第2个数与第3个数之和为36，求这4个数.

排列与组合部分

考纲内容：计数原理、排列与组合.

考纲要求：了解排列与组合的概念；掌握排列与组合的公式；能用计数原理、排列与组合知识处理简单问题.